IRBridge: Solving Image Restoration Bridge with Pre-trained Generative Diffusion Models

Bridge models in image restoration construct a diffusion process from degraded to clear images. However, existing methods typically require training a bridge model from scratch for each specific type of degradation, resulting in high computational costs and limited performance. This work aims to efficiently leverage pretrained generative priors within existing image restoration bridges to eliminate this requirement. The main challenge is that standard generative models are typically designed for a diffusion process that starts from pure noise, while restoration tasks begin with a low-quality image, resulting in a mismatch in the state distributions between the two processes. To address this challenge, we propose a transition equation that bridges two diffusion processes with the same endpoint distribution. Based on this, we introduce the IRBridge framework, which enables the direct utilization of generative models within image restoration bridges, offering a more flexible and adaptable approach to image restoration. Extensive experiments on six image restoration tasks demonstrate that IRBridge efficiently integrates generative priors, resulting in improved robustness and generalization performance. Code will be available at GitHub.

Semantic Residual for Multimodal Unified Discrete Representation

Recent research in the domain of multimodal unified representations predominantly employs codebook as representation forms, utilizing Vector Quantization(VQ) for quantization, yet there has been insufficient exploration of other quantization representation forms. Our work explores more precise quantization methods and introduces a new framework, Semantic Residual Cross-modal Information Disentanglement (SRCID), inspired by the numerical residual concept inherent to Residual Vector Quantization (RVQ). SRCID employs semantic residual-based information disentanglement for multimodal data to better handle the inherent discrepancies between different modalities. Our method enhances the capabilities of unified multimodal representations and demonstrates exceptional performance in cross-modal generalization and cross-modal zero-shot retrieval. Its average results significantly surpass existing state-of-the-art models, as well as previous attempts with RVQ and Finite Scalar Quantization (FSQ) based on these modals.

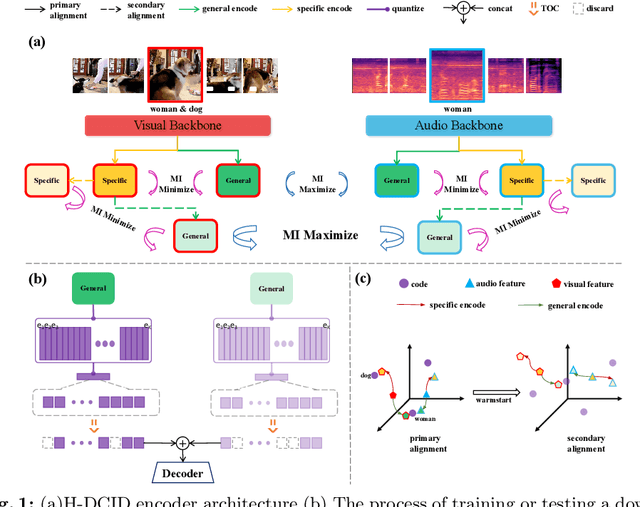
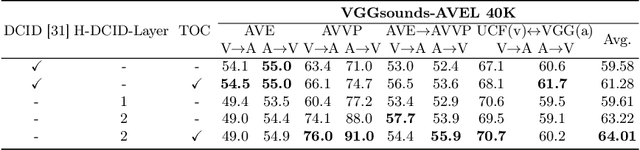
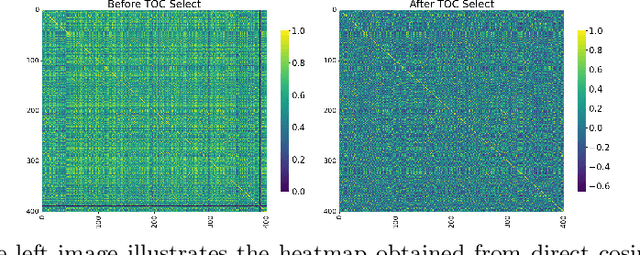
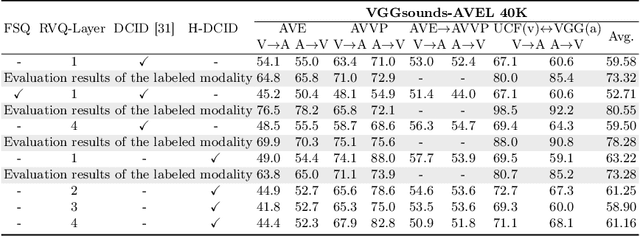
Unlocking the Potential of Multimodal Unified Discrete Representation through Training-Free Codebook Optimization and Hierarchical Alignment

Recent advances in representation learning have demonstrated the significance of multimodal alignment. The Dual Cross-modal Information Disentanglement (DCID) model, utilizing a unified codebook, shows promising results in achieving fine-grained representation and cross-modal generalization. However, it is still hindered by equal treatment of all channels and neglect of minor event information, resulting in interference from irrelevant channels and limited performance in fine-grained tasks. Thus, in this work, We propose a Training-free Optimization of Codebook (TOC) method to enhance model performance by selecting important channels in the unified space without retraining. Additionally, we introduce the Hierarchical Dual Cross-modal Information Disentanglement (H-DCID) approach to extend information separation and alignment to two levels, capturing more cross-modal details. The experiment results demonstrate significant improvements across various downstream tasks, with TOC contributing to an average improvement of 1.70% for DCID on four tasks, and H-DCID surpassing DCID by an average of 3.64%. The combination of TOC and H-DCID further enhances performance, exceeding DCID by 4.43%. These findings highlight the effectiveness of our methods in facilitating robust and nuanced cross-modal learning, opening avenues for future enhancements. The source code and pre-trained models can be accessed at https://github.com/haihuangcode/TOC_H-DCID.

Language-Codec: Reducing the Gaps Between Discrete Codec Representation and Speech Language Models

In recent years, large language models have achieved significant success in generative tasks (e.g., speech cloning and audio generation) related to speech, audio, music, and other signal domains. A crucial element of these models is the discrete acoustic codecs, which serves as an intermediate representation replacing the mel-spectrogram. However, there exist several gaps between discrete codecs and downstream speech language models. Specifically, 1) most codec models are trained on only 1,000 hours of data, whereas most speech language models are trained on 60,000 hours; 2) Achieving good reconstruction performance requires the utilization of numerous codebooks, which increases the burden on downstream speech language models; 3) The initial channel of the codebooks contains excessive information, making it challenging to directly generate acoustic tokens from weakly supervised signals such as text in downstream tasks. Consequently, leveraging the characteristics of speech language models, we propose Language-Codec. In the Language-Codec, we introduce a Mask Channel Residual Vector Quantization (MCRVQ) mechanism along with improved Fourier transform structures and larger training datasets to address the aforementioned gaps. We compare our method with competing audio compression algorithms and observe significant outperformance across extensive evaluations. Furthermore, we also validate the efficiency of the Language-Codec on downstream speech language models. The source code and pre-trained models can be accessed at https://github.com/jishengpeng/languagecodec .

On Linear Separation Capacity of Self-Supervised Representation Learning

Recent advances in self-supervised learning have highlighted the efficacy of data augmentation in learning data representation from unlabeled data. Training a linear model atop these enhanced representations can yield an adept classifier. Despite the remarkable empirical performance, the underlying mechanisms that enable data augmentation to unravel nonlinear data structures into linearly separable representations remain elusive. This paper seeks to bridge this gap by investigating under what conditions learned representations can linearly separate manifolds when data is drawn from a multi-manifold model. Our investigation reveals that data augmentation offers additional information beyond observed data and can thus improve the information-theoretic optimal rate of linear separation capacity. In particular, we show that self-supervised learning can linearly separate manifolds with a smaller distance than unsupervised learning, underscoring the additional benefits of data augmentation. Our theoretical analysis further underscores that the performance of downstream linear classifiers primarily hinges on the linear separability of data representations rather than the size of the labeled data set, reaffirming the viability of constructing efficient classifiers with limited labeled data amid an expansive unlabeled data set.

Augmentation Invariant Manifold Learning

Data augmentation is a widely used technique and an essential ingredient in the recent advance in self-supervised representation learning. By preserving the similarity between augmented data, the resulting data representation can improve various downstream analyses and achieve state-of-art performance in many applications. To demystify the role of data augmentation, we develop a statistical framework on a low-dimension product manifold to theoretically understand why the unlabeled augmented data can lead to useful data representation. Under this framework, we propose a new representation learning method called augmentation invariant manifold learning and develop the corresponding loss function, which can work with a deep neural network to learn data representations. Compared with existing methods, the new data representation simultaneously exploits the manifold's geometric structure and invariant property of augmented data. Our theoretical investigation precisely characterizes how the data representation learned from augmented data can improve the $k$-nearest neighbor classifier in the downstream analysis, showing that a more complex data augmentation leads to more improvement in downstream analysis. Finally, numerical experiments on simulated and real datasets are presented to support the theoretical results in this paper.

Self-Supervised Metric Learning in Multi-View Data: A Downstream Task Perspective

Self-supervised metric learning has been a successful approach for learning a distance from an unlabeled dataset. The resulting distance is broadly useful for improving various distance-based downstream tasks, even when no information from downstream tasks is utilized in the metric learning stage. To gain insights into this approach, we develop a statistical framework to theoretically study how self-supervised metric learning can benefit downstream tasks in the context of multi-view data. Under this framework, we show that the target distance of metric learning satisfies several desired properties for the downstream tasks. On the other hand, our investigation suggests the target distance can be further improved by moderating each direction's weights. In addition, our analysis precisely characterizes the improvement by self-supervised metric learning on four commonly used downstream tasks: sample identification, two-sample testing, $k$-means clustering, and $k$-nearest neighbor classification. As a by-product, we propose a simple spectral method for self-supervised metric learning, which is computationally efficient and minimax optimal for estimating target distance. Finally, numerical experiments are presented to support the theoretical results in the paper.

Finding Differentially Covarying Needles in a Temporally Evolving Haystack: A Scan Statistics Perspective

Recent results in coupled or temporal graphical models offer schemes for estimating the relationship structure between features when the data come from related (but distinct) longitudinal sources. A novel application of these ideas is for analyzing group-level differences, i.e., in identifying if trends of estimated objects (e.g., covariance or precision matrices) are different across disparate conditions (e.g., gender or disease). Often, poor effect sizes make detecting the differential signal over the full set of features difficult: for example, dependencies between only a subset of features may manifest differently across groups. In this work, we first give a parametric model for estimating trends in the space of SPD matrices as a function of one or more covariates. We then generalize scan statistics to graph structures, to search over distinct subsets of features (graph partitions) whose temporal dependency structure may show statistically significant group-wise differences. We theoretically analyze the Family Wise Error Rate (FWER) and bounds on Type 1 and Type 2 error. On a cohort of individuals with risk factors for Alzheimer's disease (but otherwise cognitively healthy), we find scientifically interesting group differences where the default analysis, i.e., models estimated on the full graph, do not survive reasonable significance thresholds.