Learning to Rank Normalized Entropy Curves with Differentiable Window Transformation

Recent automated machine learning systems often use learning curves ranking models to inform decisions about when to stop unpromising trials and identify better model configurations. In this paper, we present a novel learning curve ranking model specifically tailored for ranking normalized entropy (NE) learning curves, which are commonly used in online advertising and recommendation systems. Our proposed model, self-Adaptive Curve Transformation augmented Relative curve Ranking (ACTR2), features an adaptive curve transformation layer that transforms raw lifetime NE curves into composite window NE curves with the window sizes adaptively optimized based on both the position on the learning curve and the curve's dynamics. We also introduce a novel differentiable indexing method for the proposed adaptive curve transformation, which allows gradients with respect to the discrete indices to flow freely through the curve transformation layer, enabling the learned window sizes to be updated flexibly during training. Additionally, we propose a pairwise curve ranking architecture that directly models the difference between the two learning curves and is better at capturing subtle changes in relative performance that may not be evident when modeling each curve individually as the existing approaches did. Our extensive experiments on a real-world NE curve dataset demonstrate the effectiveness of each key component of ACTR2 and its improved performance over the state-of-the-art.

Does SLOPE outperform bridge regression?

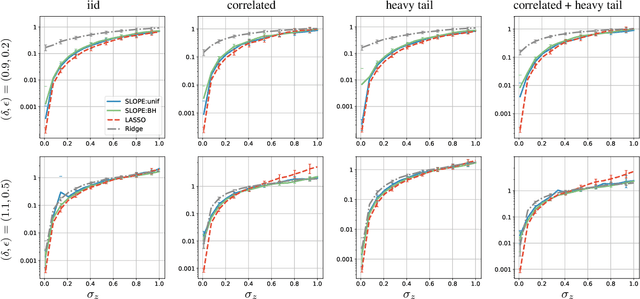
A recently proposed SLOPE estimator (arXiv:1407.3824) has been shown to adaptively achieve the minimax $\ell_2$ estimation rate under high-dimensional sparse linear regression models (arXiv:1503.08393). Such minimax optimality holds in the regime where the sparsity level $k$, sample size $n$, and dimension $p$ satisfy $k/p \rightarrow 0$, $k\log p/n \rightarrow 0$. In this paper, we characterize the estimation error of SLOPE under the complementary regime where both $k$ and $n$ scale linearly with $p$, and provide new insights into the performance of SLOPE estimators. We first derive a concentration inequality for the finite sample mean square error (MSE) of SLOPE. The quantity that MSE concentrates around takes a complicated and implicit form. With delicate analysis of the quantity, we prove that among all SLOPE estimators, LASSO is optimal for estimating $k$-sparse parameter vectors that do not have tied non-zero components in the low noise scenario. On the other hand, in the large noise scenario, the family of SLOPE estimators are sub-optimal compared with bridge regression such as the Ridge estimator.

Approximate Leave-One-Out for Fast Parameter Tuning in High Dimensions

Consider the following class of learning schemes: $$\hat{\boldsymbol{\beta}} := \arg\min_{\boldsymbol{\beta}}\;\sum_{j=1}^n \ell(\boldsymbol{x}_j^\top\boldsymbol{\beta}; y_j) + \lambda R(\boldsymbol{\beta}),\qquad\qquad (1) $$ where $\boldsymbol{x}_i \in \mathbb{R}^p$ and $y_i \in \mathbb{R}$ denote the $i^{\text{th}}$ feature and response variable respectively. Let $\ell$ and $R$ be the loss function and regularizer, $\boldsymbol{\beta}$ denote the unknown weights, and $\lambda$ be a regularization parameter. Finding the optimal choice of $\lambda$ is a challenging problem in high-dimensional regimes where both $n$ and $p$ are large. We propose two frameworks to obtain a computationally efficient approximation ALO of the leave-one-out cross validation (LOOCV) risk for nonsmooth losses and regularizers. Our two frameworks are based on the primal and dual formulations of (1). We prove the equivalence of the two approaches under smoothness conditions. This equivalence enables us to justify the accuracy of both methods under such conditions. We use our approaches to obtain a risk estimate for several standard problems, including generalized LASSO, nuclear norm regularization, and support vector machines. We empirically demonstrate the effectiveness of our results for non-differentiable cases.