Unsupervised Federated Learning: A Federated Gradient EM Algorithm for Heterogeneous Mixture Models with Robustness against Adversarial Attacks

While supervised federated learning approaches have enjoyed significant success, the domain of unsupervised federated learning remains relatively underexplored. In this paper, we introduce a novel federated gradient EM algorithm designed for the unsupervised learning of mixture models with heterogeneous mixture proportions across tasks. We begin with a comprehensive finite-sample theory that holds for general mixture models, then apply this general theory on Gaussian Mixture Models (GMMs) and Mixture of Regressions (MoRs) to characterize the explicit estimation error of model parameters and mixture proportions. Our proposed federated gradient EM algorithm demonstrates several key advantages: adaptability to unknown task similarity, resilience against adversarial attacks on a small fraction of data sources, protection of local data privacy, and computational and communication efficiency.

Unsupervised Multi-task and Transfer Learning on Gaussian Mixture Models

Unsupervised learning has been widely used in many real-world applications. One of the simplest and most important unsupervised learning models is the Gaussian mixture model (GMM). In this work, we study the multi-task learning problem on GMMs, which aims to leverage potentially similar GMM parameter structures among tasks to obtain improved learning performance compared to single-task learning. We propose a multi-task GMM learning procedure based on the EM algorithm that not only can effectively utilize unknown similarity between related tasks but is also robust against a fraction of outlier tasks from arbitrary sources. The proposed procedure is shown to achieve minimax optimal rate of convergence for both parameter estimation error and the excess mis-clustering error, in a wide range of regimes. Moreover, we generalize our approach to tackle the problem of transfer learning for GMMs, where similar theoretical results are derived. Finally, we demonstrate the effectiveness of our methods through simulations and a real data analysis. To the best of our knowledge, this is the first work studying multi-task and transfer learning on GMMs with theoretical guarantees.

Spectral clustering via adaptive layer aggregation for multi-layer networks

One of the fundamental problems in network analysis is detecting community structure in multi-layer networks, of which each layer represents one type of edge information among the nodes. We propose integrative spectral clustering approaches based on effective convex layer aggregations. Our aggregation methods are strongly motivated by a delicate asymptotic analysis of the spectral embedding of weighted adjacency matrices and the downstream $k$-means clustering, in a challenging regime where community detection consistency is impossible. In fact, the methods are shown to estimate the optimal convex aggregation, which minimizes the mis-clustering error under some specialized multi-layer network models. Our analysis further suggests that clustering using Gaussian mixture models is generally superior to the commonly used $k$-means in spectral clustering. Extensive numerical studies demonstrate that our adaptive aggregation techniques, together with Gaussian mixture model clustering, make the new spectral clustering remarkably competitive compared to several popularly used methods.

Does SLOPE outperform bridge regression?

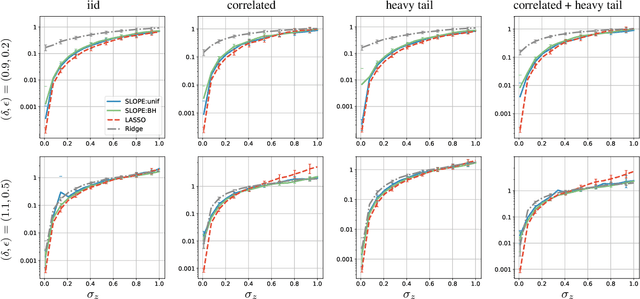
A recently proposed SLOPE estimator (arXiv:1407.3824) has been shown to adaptively achieve the minimax $\ell_2$ estimation rate under high-dimensional sparse linear regression models (arXiv:1503.08393). Such minimax optimality holds in the regime where the sparsity level $k$, sample size $n$, and dimension $p$ satisfy $k/p \rightarrow 0$, $k\log p/n \rightarrow 0$. In this paper, we characterize the estimation error of SLOPE under the complementary regime where both $k$ and $n$ scale linearly with $p$, and provide new insights into the performance of SLOPE estimators. We first derive a concentration inequality for the finite sample mean square error (MSE) of SLOPE. The quantity that MSE concentrates around takes a complicated and implicit form. With delicate analysis of the quantity, we prove that among all SLOPE estimators, LASSO is optimal for estimating $k$-sparse parameter vectors that do not have tied non-zero components in the low noise scenario. On the other hand, in the large noise scenario, the family of SLOPE estimators are sub-optimal compared with bridge regression such as the Ridge estimator.

Matrix Completion with Nonconvex Regularization: Spectral Operators and Scalable Algorithms

In this paper, we study the popularly dubbed matrix completion problem, where the task is to "fill in" the unobserved entries of a matrix from a small subset of observed entries, under the assumption that the underlying matrix is of low-rank. Our contributions herein, enhance our prior work on nuclear norm regularized problems for matrix completion (Mazumder et al., 2010) by incorporating a continuum of nonconvex penalty functions between the convex nuclear norm and nonconvex rank functions. Inspired by SOFT-IMPUTE (Mazumder et al., 2010; Hastie et al., 2016), we propose NC-IMPUTE- an EM-flavored algorithmic framework for computing a family of nonconvex penalized matrix completion problems with warm-starts. We present a systematic study of the associated spectral thresholding operators, which play an important role in the overall algorithm. We study convergence properties of the algorithm. Using structured low-rank SVD computations, we demonstrate the computational scalability of our proposal for problems up to the Netflix size (approximately, a $500,000 \times 20, 000$ matrix with $10^8$ observed entries). We demonstrate that on a wide range of synthetic and real data instances, our proposed nonconvex regularization framework leads to low-rank solutions with better predictive performance when compared to those obtained from nuclear norm problems. Implementations of algorithms proposed herein, written in the R programming language, are made available on github.

A note on estimation in a simple probit model under dependency

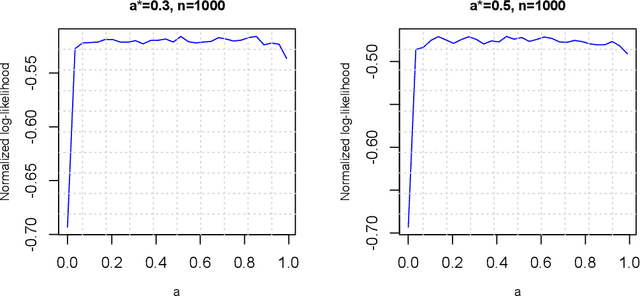
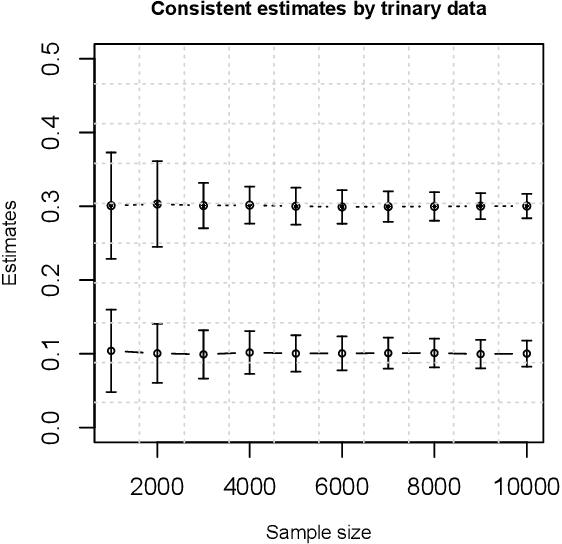
We consider a probit model without covariates, but the latent Gaussian variables having compound symmetry covariance structure with a single parameter characterizing the common correlation. We study the parameter estimation problem under such one-parameter probit models. As a surprise, we demonstrate that the likelihood function does not yield consistent estimates for the correlation. We then formally prove the parameter's nonestimability by deriving a non-vanishing minimax lower bound. This counter-intuitive phenomenon provides an interesting insight that one bit information of the latent Gaussian variables is not sufficient to consistently recover their correlation. On the other hand, we further show that trinary data generated from the Gaussian variables can consistently estimate the correlation with parametric convergence rate. Hence we reveal a phase transition phenomenon regarding the discretization of latent Gaussian variables while preserving the estimability of the correlation.