A note on estimation in a simple probit model under dependency

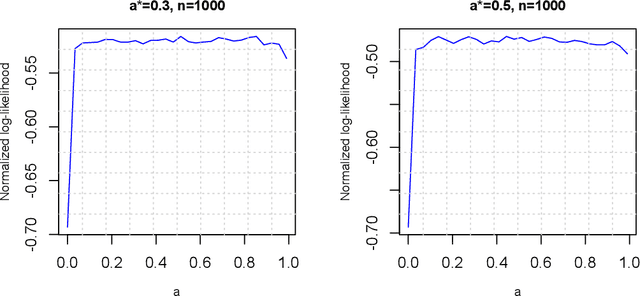
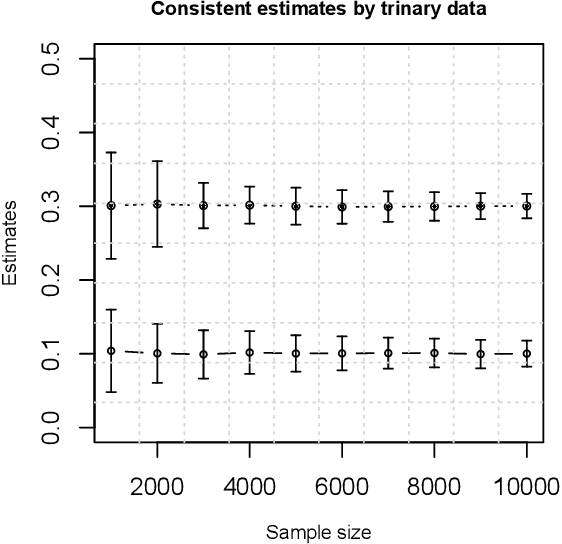
We consider a probit model without covariates, but the latent Gaussian variables having compound symmetry covariance structure with a single parameter characterizing the common correlation. We study the parameter estimation problem under such one-parameter probit models. As a surprise, we demonstrate that the likelihood function does not yield consistent estimates for the correlation. We then formally prove the parameter's nonestimability by deriving a non-vanishing minimax lower bound. This counter-intuitive phenomenon provides an interesting insight that one bit information of the latent Gaussian variables is not sufficient to consistently recover their correlation. On the other hand, we further show that trinary data generated from the Gaussian variables can consistently estimate the correlation with parametric convergence rate. Hence we reveal a phase transition phenomenon regarding the discretization of latent Gaussian variables while preserving the estimability of the correlation.