TimeCNN: Refining Cross-Variable Interaction on Time Point for Time Series Forecasting

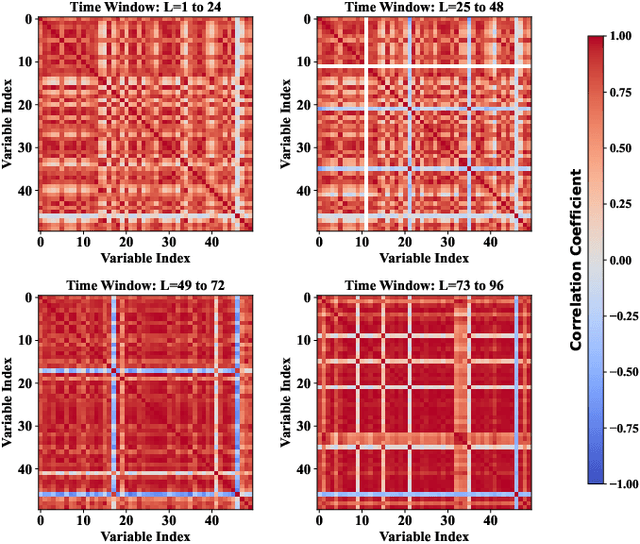
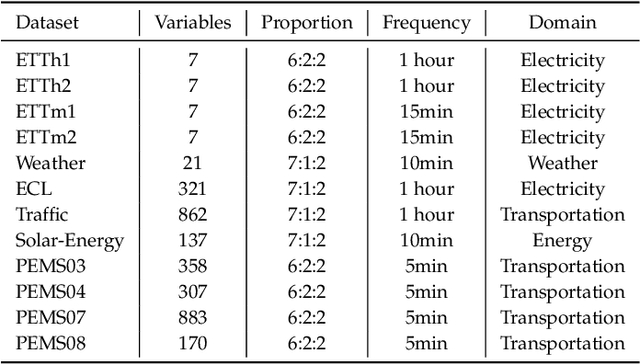
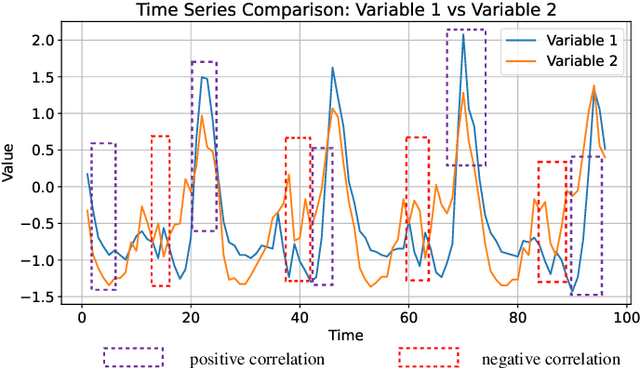
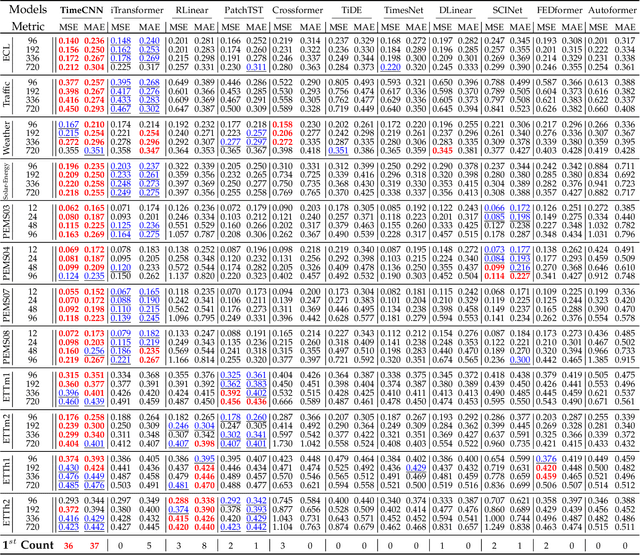
Time series forecasting is extensively applied across diverse domains. Transformer-based models demonstrate significant potential in modeling cross-time and cross-variable interaction. However, we notice that the cross-variable correlation of multivariate time series demonstrates multifaceted (positive and negative correlations) and dynamic progression over time, which is not well captured by existing Transformer-based models. To address this issue, we propose a TimeCNN model to refine cross-variable interactions to enhance time series forecasting. Its key innovation is timepoint-independent, where each time point has an independent convolution kernel, allowing each time point to have its independent model to capture relationships among variables. This approach effectively handles both positive and negative correlations and adapts to the evolving nature of variable relationships over time. Extensive experiments conducted on 12 real-world datasets demonstrate that TimeCNN consistently outperforms state-of-the-art models. Notably, our model achieves significant reductions in computational requirements (approximately 60.46%) and parameter count (about 57.50%), while delivering inference speeds 3 to 4 times faster than the benchmark iTransformer model

Enhancing Multivariate Time Series Forecasting with Mutual Information-driven Cross-Variable and Temporal Modeling

Recent advancements have underscored the impact of deep learning techniques on multivariate time series forecasting (MTSF). Generally, these techniques are bifurcated into two categories: Channel-independence and Channel-mixing approaches. Although Channel-independence methods typically yield better results, Channel-mixing could theoretically offer improvements by leveraging inter-variable correlations. Nonetheless, we argue that the integration of uncorrelated information in channel-mixing methods could curtail the potential enhancement in MTSF model performance. To substantiate this claim, we introduce the Cross-variable Decorrelation Aware feature Modeling (CDAM) for Channel-mixing approaches, aiming to refine Channel-mixing by minimizing redundant information between channels while enhancing relevant mutual information. Furthermore, we introduce the Temporal correlation Aware Modeling (TAM) to exploit temporal correlations, a step beyond conventional single-step forecasting methods. This strategy maximizes the mutual information between adjacent sub-sequences of both the forecasted and target series. Combining CDAM and TAM, our novel framework significantly surpasses existing models, including those previously considered state-of-the-art, in comprehensive tests.

PDETime: Rethinking Long-Term Multivariate Time Series Forecasting from the perspective of partial differential equations

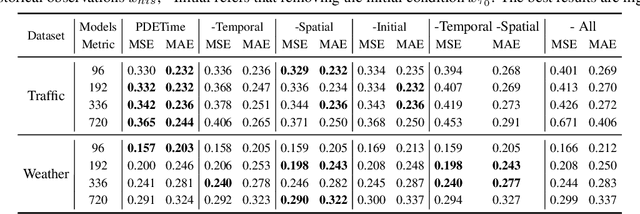
Recent advancements in deep learning have led to the development of various models for long-term multivariate time-series forecasting (LMTF), many of which have shown promising results. Generally, the focus has been on historical-value-based models, which rely on past observations to predict future series. Notably, a new trend has emerged with time-index-based models, offering a more nuanced understanding of the continuous dynamics underlying time series. Unlike these two types of models that aggregate the information of spatial domains or temporal domains, in this paper, we consider multivariate time series as spatiotemporal data regularly sampled from a continuous dynamical system, which can be represented by partial differential equations (PDEs), with the spatial domain being fixed. Building on this perspective, we present PDETime, a novel LMTF model inspired by the principles of Neural PDE solvers, following the encoding-integration-decoding operations. Our extensive experimentation across seven diverse real-world LMTF datasets reveals that PDETime not only adapts effectively to the intrinsic spatiotemporal nature of the data but also sets new benchmarks, achieving state-of-the-art results

Revisiting Long-term Time Series Forecasting: An Investigation on Linear Mapping

Long-term time series forecasting has gained significant attention in recent years. While there are various specialized designs for capturing temporal dependency, previous studies have demonstrated that a single linear layer can achieve competitive forecasting performance compared to other complex architectures. In this paper, we thoroughly investigate the intrinsic effectiveness of recent approaches and make three key observations: 1) linear mapping is critical to prior long-term time series forecasting efforts; 2) RevIN (reversible normalization) and CI (Channel Independent) play a vital role in improving overall forecasting performance; and 3) linear mapping can effectively capture periodic features in time series and has robustness for different periods across channels when increasing the input horizon. We provide theoretical and experimental explanations to support our findings and also discuss the limitations and future works. Our framework's code is available at \url{https://github.com/plumprc/RTSF}.