Deep Sparse Subspace Clustering

In this paper, we present a deep extension of Sparse Subspace Clustering, termed Deep Sparse Subspace Clustering (DSSC). Regularized by the unit sphere distribution assumption for the learned deep features, DSSC can infer a new data affinity matrix by simultaneously satisfying the sparsity principle of SSC and the nonlinearity given by neural networks. One of the appealing advantages brought by DSSC is: when original real-world data do not meet the class-specific linear subspace distribution assumption, DSSC can employ neural networks to make the assumption valid with its hierarchical nonlinear transformations. To the best of our knowledge, this is among the first deep learning based subspace clustering methods. Extensive experiments are conducted on four real-world datasets to show the proposed DSSC is significantly superior to 12 existing methods for subspace clustering.

A Unified Framework for Representation-based Subspace Clustering of Out-of-sample and Large-scale Data

Under the framework of spectral clustering, the key of subspace clustering is building a similarity graph which describes the neighborhood relations among data points. Some recent works build the graph using sparse, low-rank, and $\ell_2$-norm-based representation, and have achieved state-of-the-art performance. However, these methods have suffered from the following two limitations. First, the time complexities of these methods are at least proportional to the cube of the data size, which make those methods inefficient for solving large-scale problems. Second, they cannot cope with out-of-sample data that are not used to construct the similarity graph. To cluster each out-of-sample datum, the methods have to recalculate the similarity graph and the cluster membership of the whole data set. In this paper, we propose a unified framework which makes representation-based subspace clustering algorithms feasible to cluster both out-of-sample and large-scale data. Under our framework, the large-scale problem is tackled by converting it as out-of-sample problem in the manner of "sampling, clustering, coding, and classifying". Furthermore, we give an estimation for the error bounds by treating each subspace as a point in a hyperspace. Extensive experimental results on various benchmark data sets show that our methods outperform several recently-proposed scalable methods in clustering large-scale data set.

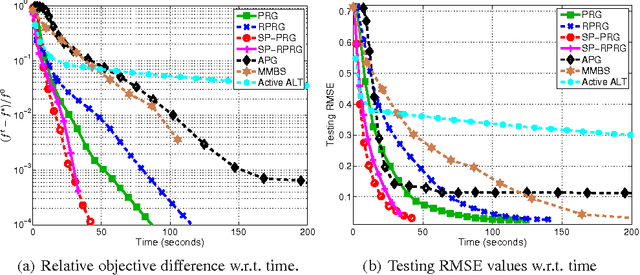
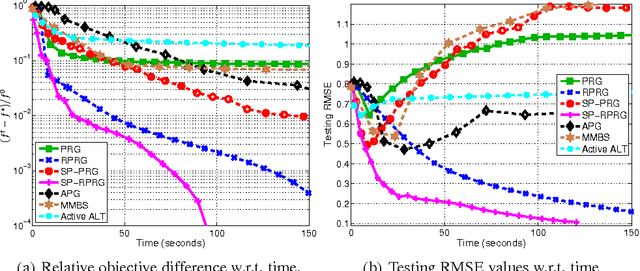
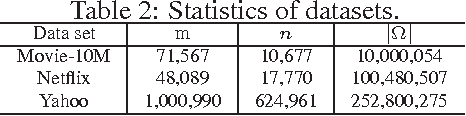
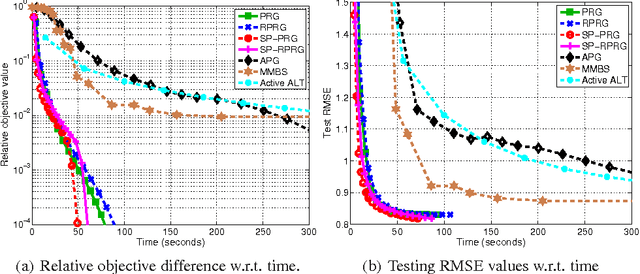
Scalable Nuclear-norm Minimization by Subspace Pursuit Proximal Riemannian Gradient

Nuclear-norm regularization plays a vital role in many learning tasks, such as low-rank matrix recovery (MR), and low-rank representation (LRR). Solving this problem directly can be computationally expensive due to the unknown rank of variables or large-rank singular value decompositions (SVDs). To address this, we propose a proximal Riemannian gradient (PRG) scheme which can efficiently solve trace-norm regularized problems defined on real-algebraic variety $\mMLr$ of real matrices of rank at most $r$. Based on PRG, we further present a simple and novel subspace pursuit (SP) paradigm for general trace-norm regularized problems without the explicit rank constraint $\mMLr$. The proposed paradigm is very scalable by avoiding large-rank SVDs. Empirical studies on several tasks, such as matrix completion and LRR based subspace clustering, demonstrate the superiority of the proposed paradigms over existing methods.