Scalable Nuclear-norm Minimization by Subspace Pursuit Proximal Riemannian Gradient
Paper and Code
Mar 18, 2015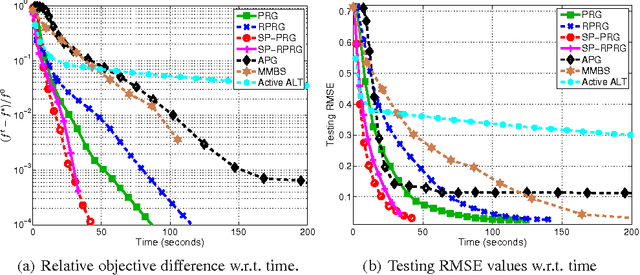
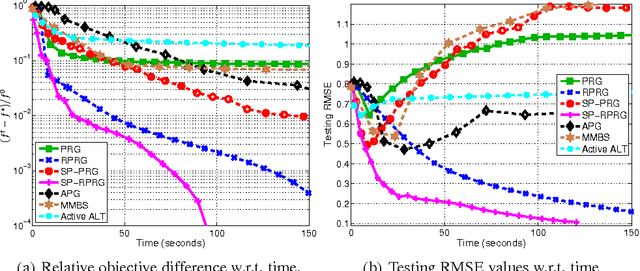
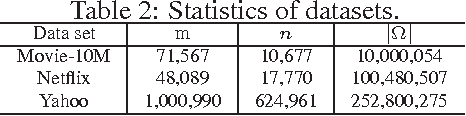
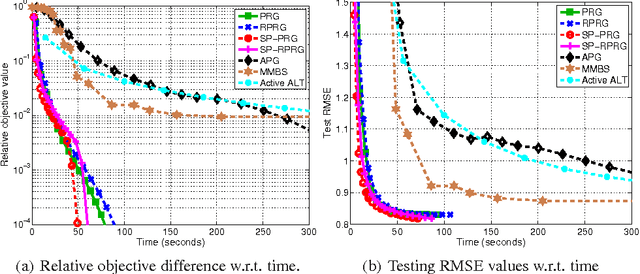
Nuclear-norm regularization plays a vital role in many learning tasks, such as low-rank matrix recovery (MR), and low-rank representation (LRR). Solving this problem directly can be computationally expensive due to the unknown rank of variables or large-rank singular value decompositions (SVDs). To address this, we propose a proximal Riemannian gradient (PRG) scheme which can efficiently solve trace-norm regularized problems defined on real-algebraic variety $\mMLr$ of real matrices of rank at most $r$. Based on PRG, we further present a simple and novel subspace pursuit (SP) paradigm for general trace-norm regularized problems without the explicit rank constraint $\mMLr$. The proposed paradigm is very scalable by avoiding large-rank SVDs. Empirical studies on several tasks, such as matrix completion and LRR based subspace clustering, demonstrate the superiority of the proposed paradigms over existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge