Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems

Advances in artificial intelligence (AI) are fueling a new paradigm of discoveries in natural sciences. Today, AI has started to advance natural sciences by improving, accelerating, and enabling our understanding of natural phenomena at a wide range of spatial and temporal scales, giving rise to a new area of research known as AI for science (AI4Science). Being an emerging research paradigm, AI4Science is unique in that it is an enormous and highly interdisciplinary area. Thus, a unified and technical treatment of this field is needed yet challenging. This paper aims to provide a technically thorough account of a subarea of AI4Science; namely, AI for quantum, atomistic, and continuum systems. These areas aim at understanding the physical world from the subatomic (wavefunctions and electron density), atomic (molecules, proteins, materials, and interactions), to macro (fluids, climate, and subsurface) scales and form an important subarea of AI4Science. A unique advantage of focusing on these areas is that they largely share a common set of challenges, thereby allowing a unified and foundational treatment. A key common challenge is how to capture physics first principles, especially symmetries, in natural systems by deep learning methods. We provide an in-depth yet intuitive account of techniques to achieve equivariance to symmetry transformations. We also discuss other common technical challenges, including explainability, out-of-distribution generalization, knowledge transfer with foundation and large language models, and uncertainty quantification. To facilitate learning and education, we provide categorized lists of resources that we found to be useful. We strive to be thorough and unified and hope this initial effort may trigger more community interests and efforts to further advance AI4Science.

A Score-Based Model for Learning Neural Wavefunctions

Quantum Monte Carlo coupled with neural network wavefunctions has shown success in computing ground states of quantum many-body systems. Existing optimization approaches compute the energy by sampling local energy from an explicit probability distribution given by the wavefunction. In this work, we provide a new optimization framework for obtaining properties of quantum many-body ground states using score-based neural networks. Our new framework does not require explicit probability distribution and performs the sampling via Langevin dynamics. Our method is based on the key observation that the local energy is directly related to scores, defined as the gradient of the logarithmic wavefunction. Inspired by the score matching and diffusion Monte Carlo methods, we derive a weighted score matching objective to guide our score-based models to converge correctly to ground states. We first evaluate our approach with experiments on quantum harmonic traps, and results show that it can accurately learn ground states of atomic systems. By implicitly modeling high-dimensional data distributions, our work paves the way toward a more efficient representation of quantum systems.

Lattice Convolutional Networks for Learning Ground States of Quantum Many-Body Systems

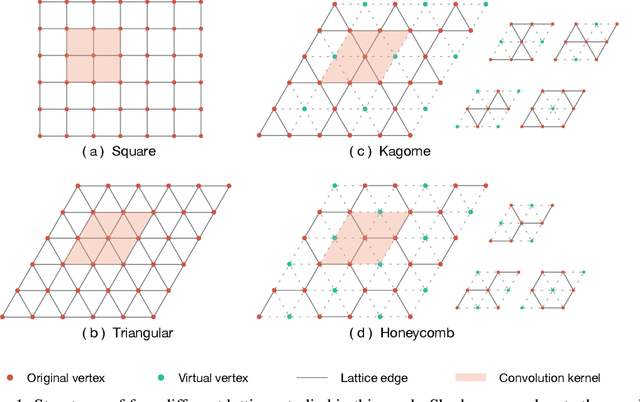
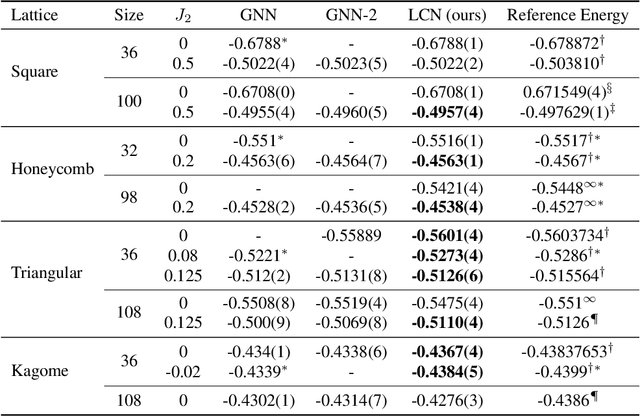
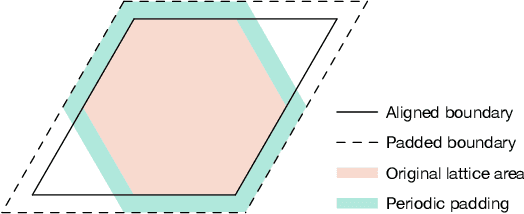
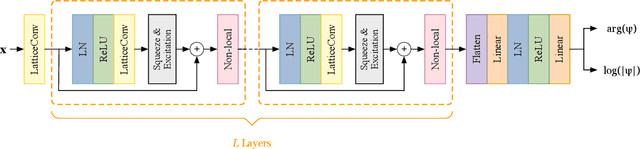
Deep learning methods have been shown to be effective in representing ground-state wave functions of quantum many-body systems. Existing methods use convolutional neural networks (CNNs) for square lattices due to their image-like structures. For non-square lattices, existing method uses graph neural network (GNN) in which structure information is not precisely captured, thereby requiring additional hand-crafted sublattice encoding. In this work, we propose lattice convolutions in which a set of proposed operations are used to convert non-square lattices into grid-like augmented lattices on which regular convolution can be applied. Based on the proposed lattice convolutions, we design lattice convolutional networks (LCN) that use self-gating and attention mechanisms. Experimental results show that our method achieves performance on par or better than existing methods on spin 1/2 $J_1$-$J_2$ Heisenberg model over the square, honeycomb, triangular, and kagome lattices while without using hand-crafted encoding.

Fast Quantum Property Prediction via Deeper 2D and 3D Graph Networks

Molecular property prediction is gaining increasing attention due to its diverse applications. One task of particular interests and importance is to predict quantum chemical properties without 3D equilibrium structures. This is practically favorable since obtaining 3D equilibrium structures requires extremely expensive calculations. In this work, we design a deep graph neural network to predict quantum properties by directly learning from 2D molecular graphs. In addition, we propose a 3D graph neural network to learn from low-cost conformer sets, which can be obtained with open-source tools using an affordable budget. We employ our methods to participate in the 2021 KDD Cup on OGB Large-Scale Challenge (OGB-LSC), which aims to predict the HOMO-LUMO energy gap of molecules. Final evaluation results reveal that we are one of the winners with a mean absolute error of 0.1235 on the holdout test set. Our implementation is available as part of the MoleculeX package (https://github.com/divelab/MoleculeX).