Lattice Convolutional Networks for Learning Ground States of Quantum Many-Body Systems
Paper and Code
Jun 15, 2022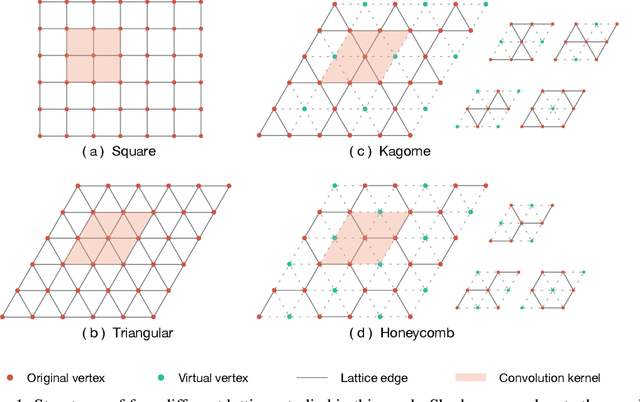
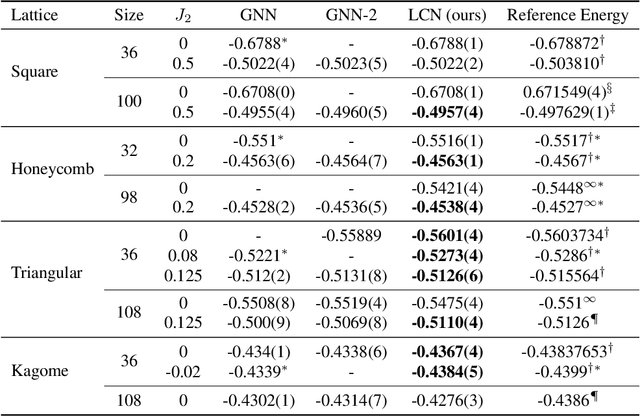
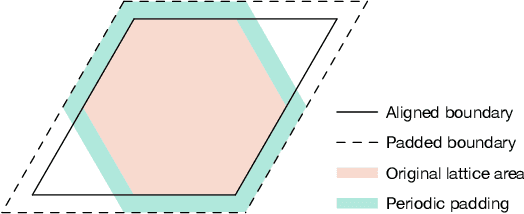
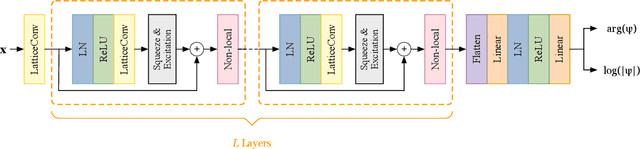
Deep learning methods have been shown to be effective in representing ground-state wave functions of quantum many-body systems. Existing methods use convolutional neural networks (CNNs) for square lattices due to their image-like structures. For non-square lattices, existing method uses graph neural network (GNN) in which structure information is not precisely captured, thereby requiring additional hand-crafted sublattice encoding. In this work, we propose lattice convolutions in which a set of proposed operations are used to convert non-square lattices into grid-like augmented lattices on which regular convolution can be applied. Based on the proposed lattice convolutions, we design lattice convolutional networks (LCN) that use self-gating and attention mechanisms. Experimental results show that our method achieves performance on par or better than existing methods on spin 1/2 $J_1$-$J_2$ Heisenberg model over the square, honeycomb, triangular, and kagome lattices while without using hand-crafted encoding.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge