Moreau Envelope for Nonconvex Bi-Level Optimization: A Single-loop and Hessian-free Solution Strategy

This work focuses on addressing two major challenges in the context of large-scale nonconvex Bi-Level Optimization (BLO) problems, which are increasingly applied in machine learning due to their ability to model nested structures. These challenges involve ensuring computational efficiency and providing theoretical guarantees. While recent advances in scalable BLO algorithms have primarily relied on lower-level convexity simplification, our work specifically tackles large-scale BLO problems involving nonconvexity in both the upper and lower levels. We simultaneously address computational and theoretical challenges by introducing an innovative single-loop gradient-based algorithm, utilizing the Moreau envelope-based reformulation, and providing non-asymptotic convergence analysis for general nonconvex BLO problems. Notably, our algorithm relies solely on first-order gradient information, enhancing its practicality and efficiency, especially for large-scale BLO learning tasks. We validate our approach's effectiveness through experiments on various synthetic problems, two typical hyper-parameter learning tasks, and a real-world neural architecture search application, collectively demonstrating its superior performance.

Constrained Bi-Level Optimization: Proximal Lagrangian Value function Approach and Hessian-free Algorithm

This paper presents a new approach and algorithm for solving a class of constrained Bi-Level Optimization (BLO) problems in which the lower-level problem involves constraints coupling both upper-level and lower-level variables. Such problems have recently gained significant attention due to their broad applicability in machine learning. However, conventional gradient-based methods unavoidably rely on computationally intensive calculations related to the Hessian matrix. To address this challenge, we begin by devising a smooth proximal Lagrangian value function to handle the constrained lower-level problem. Utilizing this construct, we introduce a single-level reformulation for constrained BLOs that transforms the original BLO problem into an equivalent optimization problem with smooth constraints. Enabled by this reformulation, we develop a Hessian-free gradient-based algorithm-termed proximal Lagrangian Value function-based Hessian-free Bi-level Algorithm (LV-HBA)-that is straightforward to implement in a single loop manner. Consequently, LV-HBA is especially well-suited for machine learning applications. Furthermore, we offer non-asymptotic convergence analysis for LV-HBA, eliminating the need for traditional strong convexity assumptions for the lower-level problem while also being capable of accommodating non-singleton scenarios. Empirical results substantiate the algorithm's superior practical performance.

Moreau Envelope Based Difference-of-weakly-Convex Reformulation and Algorithm for Bilevel Programs

Recently, Ye et al. (Mathematical Programming 2023) designed an algorithm for solving a specific class of bilevel programs with an emphasis on applications related to hyperparameter selection, utilizing the difference of convex algorithm based on the value function approach reformulation. The proposed algorithm is particularly powerful when the lower level problem is fully convex , such as a support vector machine model or a least absolute shrinkage and selection operator model. In this paper, to suit more applications related to machine learning and statistics, we substantially weaken the underlying assumption from lower level full convexity to weak convexity. Accordingly, we propose a new reformulation using Moreau envelope of the lower level problem and demonstrate that this reformulation is a difference of weakly convex program. Subsequently, we develop a sequentially convergent algorithm for solving this difference of weakly convex program. To evaluate the effectiveness of our approach, we conduct numerical experiments on the bilevel hyperparameter selection problem from elastic net, sparse group lasso, and RBF kernel support vector machine models.

Hierarchical Optimization-Derived Learning

In recent years, by utilizing optimization techniques to formulate the propagation of deep model, a variety of so-called Optimization-Derived Learning (ODL) approaches have been proposed to address diverse learning and vision tasks. Although having achieved relatively satisfying practical performance, there still exist fundamental issues in existing ODL methods. In particular, current ODL methods tend to consider model construction and learning as two separate phases, and thus fail to formulate their underlying coupling and depending relationship. In this work, we first establish a new framework, named Hierarchical ODL (HODL), to simultaneously investigate the intrinsic behaviors of optimization-derived model construction and its corresponding learning process. Then we rigorously prove the joint convergence of these two sub-tasks, from the perspectives of both approximation quality and stationary analysis. To our best knowledge, this is the first theoretical guarantee for these two coupled ODL components: optimization and learning. We further demonstrate the flexibility of our framework by applying HODL to challenging learning tasks, which have not been properly addressed by existing ODL methods. Finally, we conduct extensive experiments on both synthetic data and real applications in vision and other learning tasks to verify the theoretical properties and practical performance of HODL in various application scenarios.

Averaged Method of Multipliers for Bi-Level Optimization without Lower-Level Strong Convexity

Gradient methods have become mainstream techniques for Bi-Level Optimization (BLO) in learning fields. The validity of existing works heavily rely on either a restrictive Lower- Level Strong Convexity (LLSC) condition or on solving a series of approximation subproblems with high accuracy or both. In this work, by averaging the upper and lower level objectives, we propose a single loop Bi-level Averaged Method of Multipliers (sl-BAMM) for BLO that is simple yet efficient for large-scale BLO and gets rid of the limited LLSC restriction. We further provide non-asymptotic convergence analysis of sl-BAMM towards KKT stationary points, and the comparative advantage of our analysis lies in the absence of strong gradient boundedness assumption, which is always required by others. Thus our theory safely captures a wider variety of applications in deep learning, especially where the upper-level objective is quadratic w.r.t. the lower-level variable. Experimental results demonstrate the superiority of our method.

Optimization-Derived Learning with Essential Convergence Analysis of Training and Hyper-training

Recently, Optimization-Derived Learning (ODL) has attracted attention from learning and vision areas, which designs learning models from the perspective of optimization. However, previous ODL approaches regard the training and hyper-training procedures as two separated stages, meaning that the hyper-training variables have to be fixed during the training process, and thus it is also impossible to simultaneously obtain the convergence of training and hyper-training variables. In this work, we design a Generalized Krasnoselskii-Mann (GKM) scheme based on fixed-point iterations as our fundamental ODL module, which unifies existing ODL methods as special cases. Under the GKM scheme, a Bilevel Meta Optimization (BMO) algorithmic framework is constructed to solve the optimal training and hyper-training variables together. We rigorously prove the essential joint convergence of the fixed-point iteration for training and the process of optimizing hyper-parameters for hyper-training, both on the approximation quality, and on the stationary analysis. Experiments demonstrate the efficiency of BMO with competitive performance on sparse coding and real-world applications such as image deconvolution and rain streak removal.

Value Function Based Difference-of-Convex Algorithm for Bilevel Hyperparameter Selection Problems

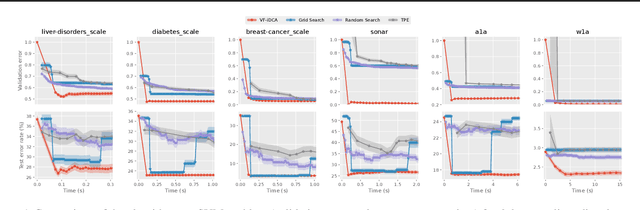
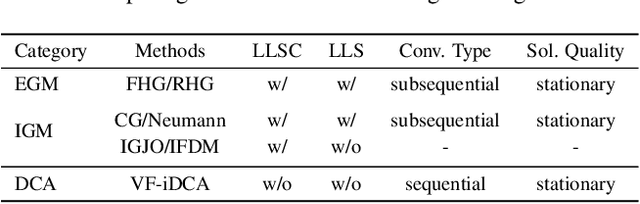
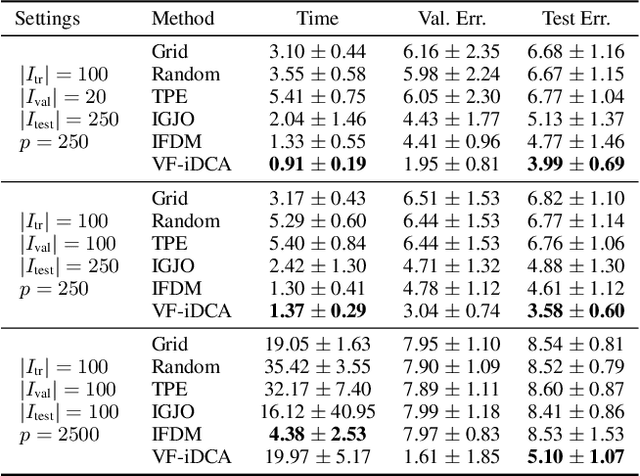
Gradient-based optimization methods for hyperparameter tuning guarantee theoretical convergence to stationary solutions when for fixed upper-level variable values, the lower level of the bilevel program is strongly convex (LLSC) and smooth (LLS). This condition is not satisfied for bilevel programs arising from tuning hyperparameters in many machine learning algorithms. In this work, we develop a sequentially convergent Value Function based Difference-of-Convex Algorithm with inexactness (VF-iDCA). We show that this algorithm achieves stationary solutions without LLSC and LLS assumptions for bilevel programs from a broad class of hyperparameter tuning applications. Our extensive experiments confirm our theoretical findings and show that the proposed VF-iDCA yields superior performance when applied to tune hyperparameters.

Towards Extremely Fast Bilevel Optimization with Self-governed Convergence Guarantees

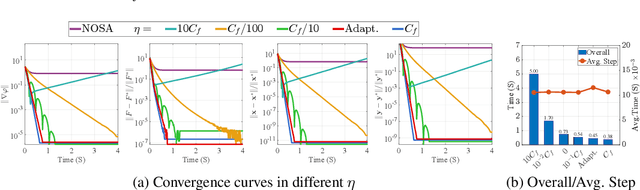
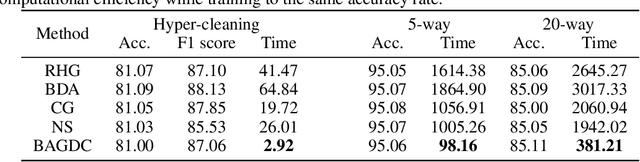
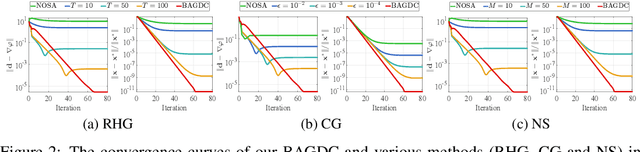
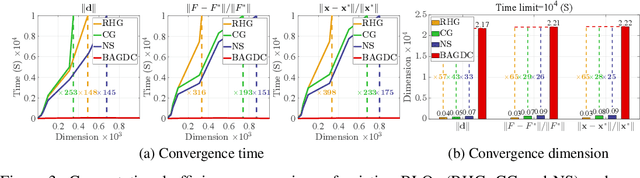
Gradient methods have become mainstream techniques for Bi-Level Optimization (BLO) in learning and vision fields. The validity of existing works heavily relies on solving a series of approximation subproblems with extraordinarily high accuracy. Unfortunately, to achieve the approximation accuracy requires executing a large quantity of time-consuming iterations and computational burden is naturally caused. This paper is thus devoted to address this critical computational issue. In particular, we propose a single-level formulation to uniformly understand existing explicit and implicit Gradient-based BLOs (GBLOs). This together with our designed counter-example can clearly illustrate the fundamental numerical and theoretical issues of GBLOs and their naive accelerations. By introducing the dual multipliers as a new variable, we then establish Bilevel Alternating Gradient with Dual Correction (BAGDC), a general framework, which significantly accelerates different categories of existing methods by taking specific settings. A striking feature of our convergence result is that, compared to those original unaccelerated GBLO versions, the fast BAGDC admits a unified non-asymptotic convergence theory towards stationarity. A variety of numerical experiments have also been conducted to demonstrate the superiority of the proposed algorithmic framework.

Value-Function-based Sequential Minimization for Bi-level Optimization

Gradient-based Bi-Level Optimization (BLO) methods have been widely applied to solve modern machine learning problems. However, most existing solution strategies are theoretically designed based on restrictive assumptions (e.g., convexity of the lower-level sub-problem), and computationally not applicable for high-dimensional tasks. Moreover, there are almost no gradient-based methods that can efficiently handle BLO in those challenging scenarios, such as BLO with functional constraints and pessimistic BLO. In this work, by reformulating BLO into an approximated single-level problem based on the value-function, we provide a new method, named Bi-level Value-Function-based Sequential Minimization (BVFSM), to partially address the above issues. To be specific, BVFSM constructs a series of value-function-based approximations, and thus successfully avoids the repeated calculations of recurrent gradient and Hessian inverse required by existing approaches, which are time-consuming (especially for high-dimensional tasks). We also extend BVFSM to address BLO with additional upper- and lower-level functional constraints. More importantly, we demonstrate that the algorithmic framework of BVFSM can also be used for the challenging pessimistic BLO, which has never been properly solved by existing gradient-based methods. On the theoretical side, we strictly prove the convergence of BVFSM on these types of BLO, in which the restrictive lower-level convexity assumption is completely discarded. To our best knowledge, this is the first gradient-based algorithm that can solve different kinds of BLO problems (e.g., optimistic, pessimistic and with constraints) all with solid convergence guarantees. Extensive experiments verify our theoretical investigations and demonstrate the superiority of BVFSM on various real-world applications.

Towards Gradient-based Bilevel Optimization with Non-convex Followers and Beyond

In recent years, Bi-Level Optimization (BLO) techniques have received extensive attentions from both learning and vision communities. A variety of BLO models in complex and practical tasks are of non-convex follower structure in nature (a.k.a., without Lower-Level Convexity, LLC for short). However, this challenging class of BLOs is lack of developments on both efficient solution strategies and solid theoretical guarantees. In this work, we propose a new algorithmic framework, named Initialization Auxiliary and Pessimistic Trajectory Truncated Gradient Method (IAPTT-GM), to partially address the above issues. In particular, by introducing an auxiliary as initialization to guide the optimization dynamics and designing a pessimistic trajectory truncation operation, we construct a reliable approximate version of the original BLO in the absence of LLC hypothesis. Our theoretical investigations establish the convergence of solutions returned by IAPTT-GM towards those of the original BLO without LLC. As an additional bonus, we also theoretically justify the quality of our IAPTT-GM embedded with Nesterov's accelerated dynamics under LLC. The experimental results confirm both the convergence of our algorithm without LLC, and the theoretical findings under LLC.