Moreau Envelope Based Difference-of-weakly-Convex Reformulation and Algorithm for Bilevel Programs

Recently, Ye et al. (Mathematical Programming 2023) designed an algorithm for solving a specific class of bilevel programs with an emphasis on applications related to hyperparameter selection, utilizing the difference of convex algorithm based on the value function approach reformulation. The proposed algorithm is particularly powerful when the lower level problem is fully convex , such as a support vector machine model or a least absolute shrinkage and selection operator model. In this paper, to suit more applications related to machine learning and statistics, we substantially weaken the underlying assumption from lower level full convexity to weak convexity. Accordingly, we propose a new reformulation using Moreau envelope of the lower level problem and demonstrate that this reformulation is a difference of weakly convex program. Subsequently, we develop a sequentially convergent algorithm for solving this difference of weakly convex program. To evaluate the effectiveness of our approach, we conduct numerical experiments on the bilevel hyperparameter selection problem from elastic net, sparse group lasso, and RBF kernel support vector machine models.

Value Function Based Difference-of-Convex Algorithm for Bilevel Hyperparameter Selection Problems

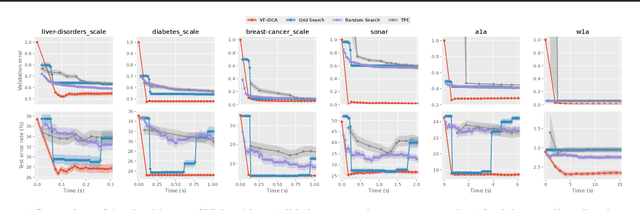
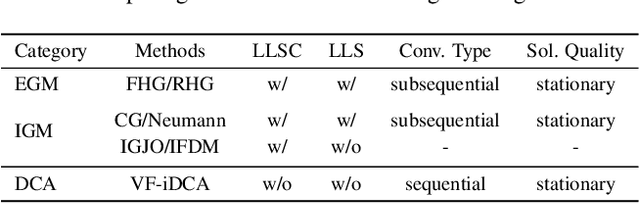
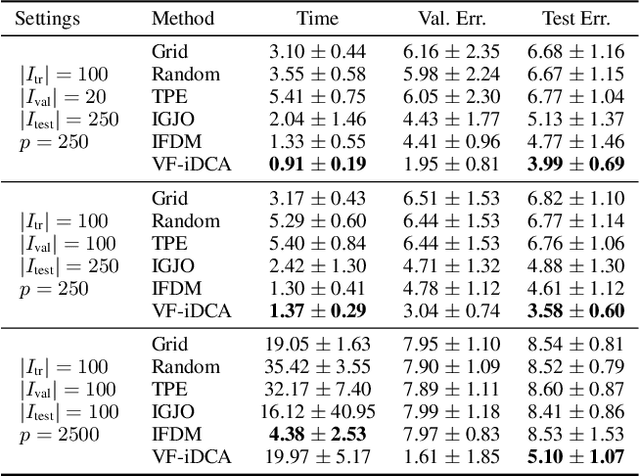
Gradient-based optimization methods for hyperparameter tuning guarantee theoretical convergence to stationary solutions when for fixed upper-level variable values, the lower level of the bilevel program is strongly convex (LLSC) and smooth (LLS). This condition is not satisfied for bilevel programs arising from tuning hyperparameters in many machine learning algorithms. In this work, we develop a sequentially convergent Value Function based Difference-of-Convex Algorithm with inexactness (VF-iDCA). We show that this algorithm achieves stationary solutions without LLSC and LLS assumptions for bilevel programs from a broad class of hyperparameter tuning applications. Our extensive experiments confirm our theoretical findings and show that the proposed VF-iDCA yields superior performance when applied to tune hyperparameters.