Discovering Sparse Recovery Algorithms Using Neural Architecture Search

The design of novel algorithms for solving inverse problems in signal processing is an incredibly difficult, heuristic-driven, and time-consuming task. In this short paper, we the idea of automated algorithm discovery in the signal processing context through meta-learning tools such as Neural Architecture Search (NAS). Specifically, we examine the Iterative Shrinkage Thresholding Algorithm (ISTA) and its accelerated Fast ISTA (FISTA) variant as candidates for algorithm rediscovery. We develop a meta-learning framework which is capable of rediscovering (several key elements of) the two aforementioned algorithms when given a search space of over 50,000 variables. We then show how our framework can apply to various data distributions and algorithms besides ISTA/FISTA.

AutoComb: Automated Comb Sign Detector for 3D CTE Scans

Comb Sign is an important imaging biomarker to detect multiple gastrointestinal diseases. It shows up as increased blood flow along the intestinal wall indicating potential abnormality, which helps doctors diagnose inflammatory conditions. Despite its clinical significance, current detection methods are manual, time-intensive, and prone to subjective interpretation due to the need for multi-planar image-orientation. To the best of our knowledge, we are the first to propose a fully automated technique for the detection of Comb Sign from CTE scans. Our novel approach is based on developing a probabilistic map that shows areas of pathological hypervascularity by identifying fine vascular bifurcations and wall enhancement via processing through stepwise algorithmic modules. These modules include utilising deep learning segmentation model, a Gaussian Mixture Model (GMM), vessel extraction using vesselness filter, iterative probabilistic enhancement of vesselness via neighborhood maximization and a distance-based weighting scheme over the vessels. Experimental results demonstrate that our pipeline effectively identifies Comb Sign, offering an objective, accurate, and reliable tool to enhance diagnostic accuracy in Crohn's disease and related hypervascular conditions where Comb Sign is considered as one of the important biomarkers.

Pruning as a Defense: Reducing Memorization in Large Language Models

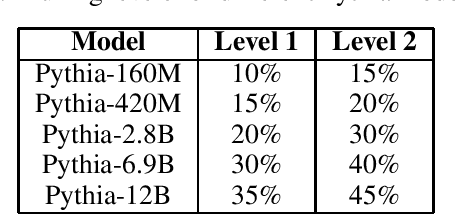
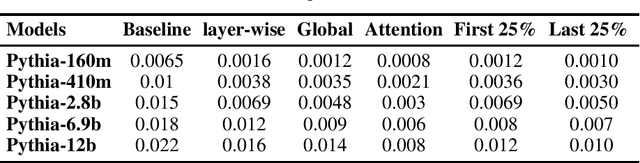
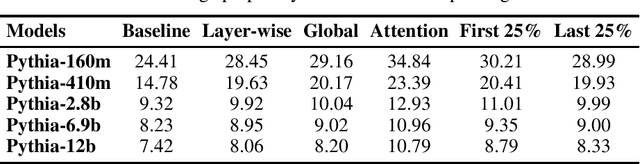
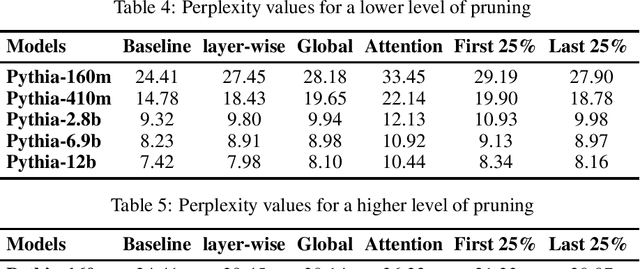
Large language models have been shown to memorize significant portions of their training data, which they can reproduce when appropriately prompted. This work investigates the impact of simple pruning techniques on this behavior. Our findings reveal that pruning effectively reduces the extent of memorization in LLMs, demonstrating its potential as a foundational approach for mitigating membership inference attacks.

WavePulse: Real-time Content Analytics of Radio Livestreams

Radio remains a pervasive medium for mass information dissemination, with AM/FM stations reaching more Americans than either smartphone-based social networking or live television. Increasingly, radio broadcasts are also streamed online and accessed over the Internet. We present WavePulse, a framework that records, documents, and analyzes radio content in real-time. While our framework is generally applicable, we showcase the efficacy of WavePulse in a collaborative project with a team of political scientists focusing on the 2024 Presidential Elections. We use WavePulse to monitor livestreams of 396 news radio stations over a period of three months, processing close to 500,000 hours of audio streams. These streams were converted into time-stamped, diarized transcripts and analyzed to track answer key political science questions at both the national and state levels. Our analysis revealed how local issues interacted with national trends, providing insights into information flow. Our results demonstrate WavePulse's efficacy in capturing and analyzing content from radio livestreams sourced from the Web. Code and dataset can be accessed at \url{https://wave-pulse.io}.

Accelerated Smoothing: A Scalable Approach to Randomized Smoothing

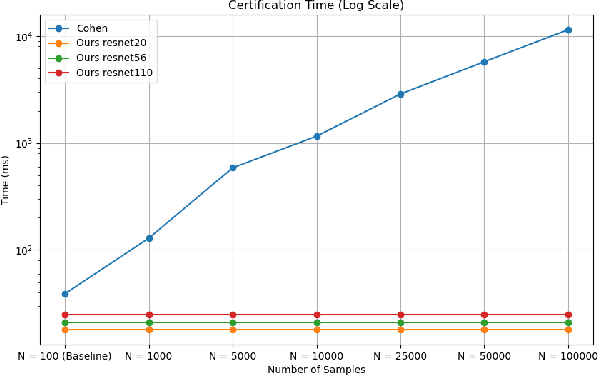
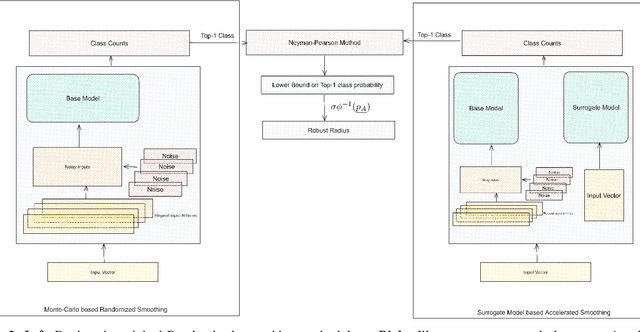
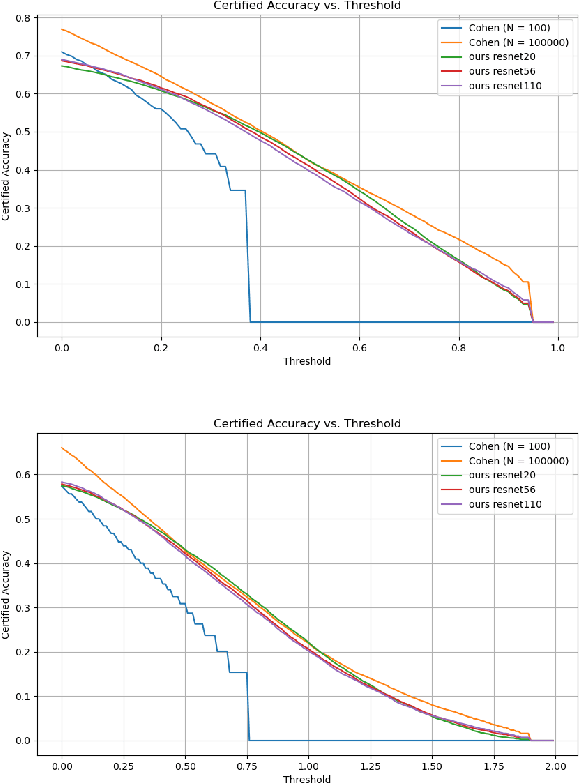
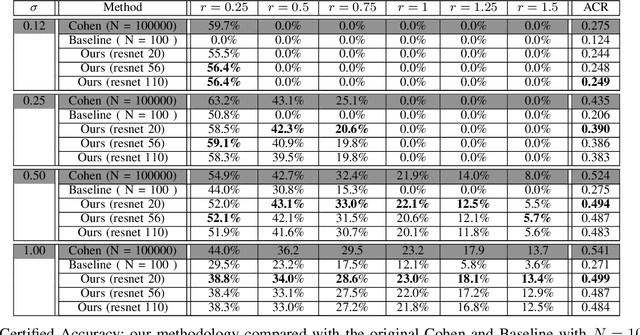
Randomized smoothing has emerged as a potent certifiable defense against adversarial attacks by employing smoothing noises from specific distributions to ensure the robustness of a smoothed classifier. However, the utilization of Monte Carlo sampling in this process introduces a compute-intensive element, which constrains the practicality of randomized smoothing on a larger scale. To address this limitation, we propose a novel approach that replaces Monte Carlo sampling with the training of a surrogate neural network. Through extensive experimentation in various settings, we demonstrate the efficacy of our approach in approximating the smoothed classifier with remarkable precision. Furthermore, we demonstrate that our approach significantly accelerates the robust radius certification process, providing nearly $600$X improvement in computation time, overcoming the computational bottlenecks associated with traditional randomized smoothing.

Trust, But Verify: A Survey of Randomized Smoothing Techniques

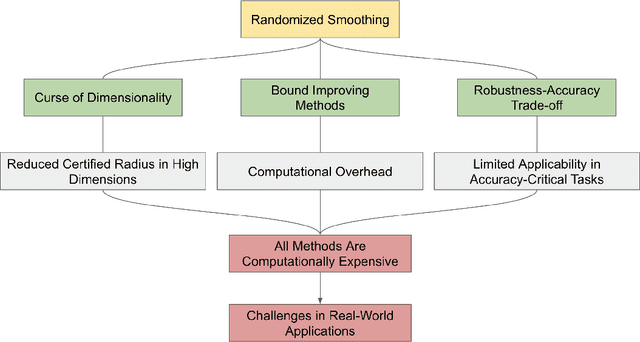
Machine learning models have demonstrated remarkable success across diverse domains but remain vulnerable to adversarial attacks. Empirical defence mechanisms often fall short, as new attacks constantly emerge, rendering existing defences obsolete. A paradigm shift from empirical defences to certification-based defences has been observed in response. Randomized smoothing has emerged as a promising technique among notable advancements. This study reviews the theoretical foundations, empirical effectiveness, and applications of randomized smoothing in verifying machine learning classifiers. We provide an in-depth exploration of the fundamental concepts underlying randomized smoothing, highlighting its theoretical guarantees in certifying robustness against adversarial perturbations. Additionally, we discuss the challenges of existing methodologies and offer insightful perspectives on potential solutions. This paper is novel in its attempt to systemise the existing knowledge in the context of randomized smoothing.

Rapid Training Data Creation by Synthesizing Medical Images for Classification and Localization

While the use of artificial intelligence (AI) for medical image analysis is gaining wide acceptance, the expertise, time and cost required to generate annotated data in the medical field are significantly high, due to limited availability of both data and expert annotation. Strongly supervised object localization models require data that is exhaustively annotated, meaning all objects of interest in an image are identified. This is difficult to achieve and verify for medical images. We present a method for the transformation of real data to train any Deep Neural Network to solve the above problems. We show the efficacy of this approach on both a weakly supervised localization model and a strongly supervised localization model. For the weakly supervised model, we show that the localization accuracy increases significantly using the generated data. For the strongly supervised model, this approach overcomes the need for exhaustive annotation on real images. In the latter model, we show that the accuracy, when trained with generated images, closely parallels the accuracy when trained with exhaustively annotated real images. The results are demonstrated on images of human urine samples obtained using microscopy.

[Re] Double Sampling Randomized Smoothing

This paper is a contribution to the reproducibility challenge in the field of machine learning, specifically addressing the issue of certifying the robustness of neural networks (NNs) against adversarial perturbations. The proposed Double Sampling Randomized Smoothing (DSRS) framework overcomes the limitations of existing methods by using an additional smoothing distribution to improve the robustness certification. The paper provides a clear manifestation of DSRS for a generalized family of Gaussian smoothing and a computationally efficient method for implementation. The experiments on MNIST and CIFAR-10 demonstrate the effectiveness of DSRS, consistently certifying larger robust radii compared to other methods. Also various ablations studies are conducted to further analyze the hyperparameters and effect of adversarial training methods on the certified radius by the proposed framework.

Scalable Optimal Design of Incremental Volt/VAR Control using Deep Neural Networks

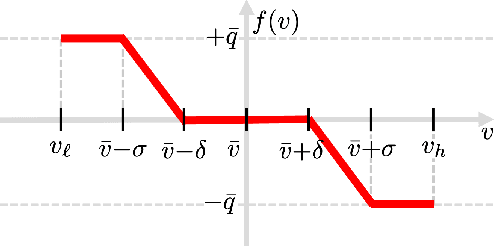
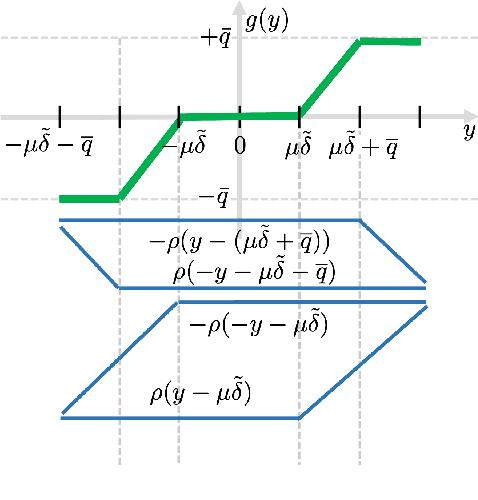
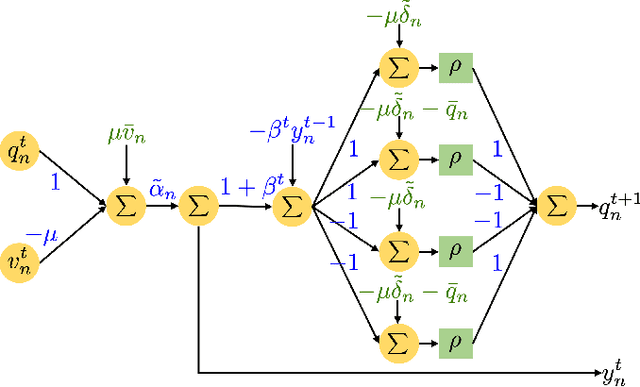
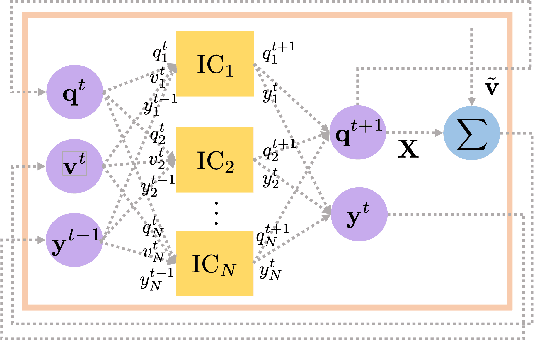
Volt/VAR control rules facilitate the autonomous operation of distributed energy resources (DER) to regulate voltage in power distribution grids. According to non-incremental control rules, such as the one mandated by the IEEE Standard 1547, the reactive power setpoint of each DER is computed as a piecewise-linear curve of the local voltage. However, the slopes of such curves are upper-bounded to ensure stability. On the other hand, incremental rules add a memory term into the setpoint update, rendering them universally stable. They can thus attain enhanced steady-state voltage profiles. Optimal rule design (ORD) for incremental rules can be formulated as a bilevel program. We put forth a scalable solution by reformulating ORD as training a deep neural network (DNN). This DNN emulates the Volt/VAR dynamics for incremental rules derived as iterations of proximal gradient descent (PGD). Analytical findings and numerical tests corroborate that the proposed ORD solution can be neatly adapted to single/multi-phase feeders.

Deep Learning for Optimal Volt/VAR Control using Distributed Energy Resources

Given their intermittency, distributed energy resources (DERs) have been commissioned with regulating voltages at fast timescales. Although the IEEE 1547 standard specifies the shape of Volt/VAR control rules, it is not clear how to optimally customize them per DER. Optimal rule design (ORD) is a challenging problem as Volt/VAR rules introduce nonlinear dynamics, require bilinear optimization models, and lurk trade-offs between stability and steady-state performance. To tackle ORD, we develop a deep neural network (DNN) that serves as a digital twin of Volt/VAR dynamics. The DNN takes grid conditions as inputs, uses rule parameters as weights, and computes equilibrium voltages as outputs. Thanks to this genuine design, ORD is reformulated as a deep learning task using grid scenarios as training data and aiming at driving the predicted variables being the equilibrium voltages close to unity. The learning task is solved by modifying efficient deep-learning routines to enforce constraints on rule parameters. In the course of DNN-based ORD, we also review and expand on stability conditions and convergence rates for Volt/VAR rules on single-/multi-phase feeders. To benchmark the optimality and runtime of DNN-based ORD, we also devise a novel mixed-integer nonlinear program formulation. Numerical tests showcase the merits of DNN-based ORD.