Ali Mehrizi-Sani
Scalable Optimal Design of Incremental Volt/VAR Control using Deep Neural Networks
Jan 04, 2023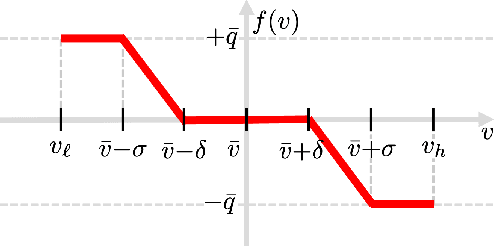
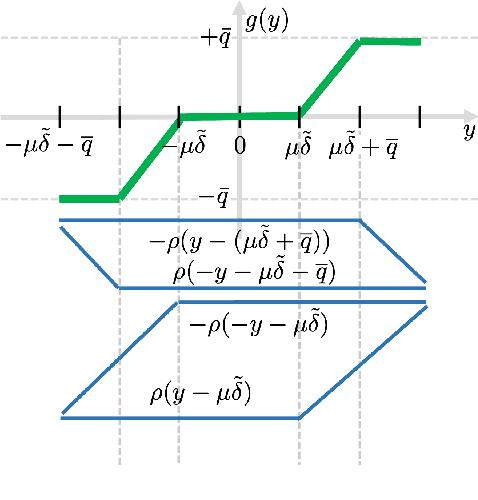
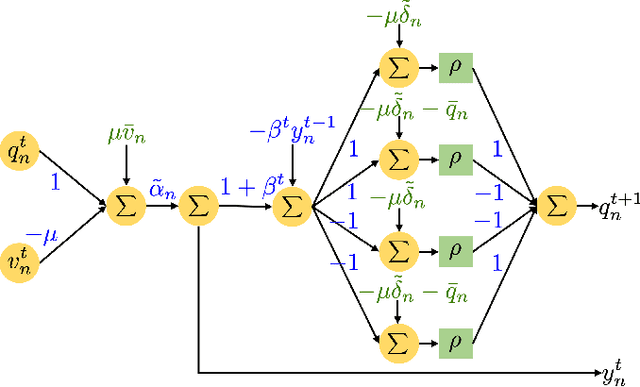
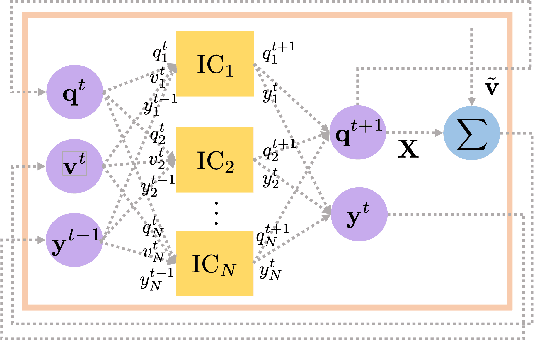
Abstract:Volt/VAR control rules facilitate the autonomous operation of distributed energy resources (DER) to regulate voltage in power distribution grids. According to non-incremental control rules, such as the one mandated by the IEEE Standard 1547, the reactive power setpoint of each DER is computed as a piecewise-linear curve of the local voltage. However, the slopes of such curves are upper-bounded to ensure stability. On the other hand, incremental rules add a memory term into the setpoint update, rendering them universally stable. They can thus attain enhanced steady-state voltage profiles. Optimal rule design (ORD) for incremental rules can be formulated as a bilevel program. We put forth a scalable solution by reformulating ORD as training a deep neural network (DNN). This DNN emulates the Volt/VAR dynamics for incremental rules derived as iterations of proximal gradient descent (PGD). Analytical findings and numerical tests corroborate that the proposed ORD solution can be neatly adapted to single/multi-phase feeders.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge