NVIDIA Nemotron 3: Efficient and Open Intelligence

We introduce the Nemotron 3 family of models - Nano, Super, and Ultra. These models deliver strong agentic, reasoning, and conversational capabilities. The Nemotron 3 family uses a Mixture-of-Experts hybrid Mamba-Transformer architecture to provide best-in-class throughput and context lengths of up to 1M tokens. Super and Ultra models are trained with NVFP4 and incorporate LatentMoE, a novel approach that improves model quality. The two larger models also include MTP layers for faster text generation. All Nemotron 3 models are post-trained using multi-environment reinforcement learning enabling reasoning, multi-step tool use, and support granular reasoning budget control. Nano, the smallest model, outperforms comparable models in accuracy while remaining extremely cost-efficient for inference. Super is optimized for collaborative agents and high-volume workloads such as IT ticket automation. Ultra, the largest model, provides state-of-the-art accuracy and reasoning performance. Nano is released together with its technical report and this white paper, while Super and Ultra will follow in the coming months. We will openly release the model weights, pre- and post-training software, recipes, and all data for which we hold redistribution rights.

Nemotron 3 Nano: Open, Efficient Mixture-of-Experts Hybrid Mamba-Transformer Model for Agentic Reasoning

We present Nemotron 3 Nano 30B-A3B, a Mixture-of-Experts hybrid Mamba-Transformer language model. Nemotron 3 Nano was pretrained on 25 trillion text tokens, including more than 3 trillion new unique tokens over Nemotron 2, followed by supervised fine tuning and large-scale RL on diverse environments. Nemotron 3 Nano achieves better accuracy than our previous generation Nemotron 2 Nano while activating less than half of the parameters per forward pass. It achieves up to 3.3x higher inference throughput than similarly-sized open models like GPT-OSS-20B and Qwen3-30B-A3B-Thinking-2507, while also being more accurate on popular benchmarks. Nemotron 3 Nano demonstrates enhanced agentic, reasoning, and chat abilities and supports context lengths up to 1M tokens. We release both our pretrained Nemotron 3 Nano 30B-A3B Base and post-trained Nemotron 3 Nano 30B-A3B checkpoints on Hugging Face.

SeedLM: Compressing LLM Weights into Seeds of Pseudo-Random Generators

Large Language Models (LLMs) have transformed natural language processing, but face significant challenges in widespread deployment due to their high runtime cost. In this paper, we introduce SeedLM, a novel post-training compression method that uses seeds of pseudo-random generators to encode and compress model weights. Specifically, for each block of weights, we find a seed that is fed into a Linear Feedback Shift Register (LFSR) during inference to efficiently generate a random matrix. This matrix is then linearly combined with compressed coefficients to reconstruct the weight block. SeedLM reduces memory access and leverages idle compute cycles during inference, effectively speeding up memory-bound tasks by trading compute for fewer memory accesses. Unlike state-of-the-art compression methods that rely on calibration data, our approach is data-free and generalizes well across diverse tasks. Our experiments with Llama 3 70B, which is particularly challenging to compress, show that SeedLM achieves significantly better zero-shot accuracy retention at 4- and 3-bit than state-of-the-art techniques, while maintaining performance comparable to FP16 baselines. Additionally, FPGA-based tests demonstrate that 4-bit SeedLM, as model size increases to 70B, approaches a 4x speed-up over an FP16 Llama 2/3 baseline.

Microscaling Data Formats for Deep Learning

Narrow bit-width data formats are key to reducing the computational and storage costs of modern deep learning applications. This paper evaluates Microscaling (MX) data formats that combine a per-block scaling factor with narrow floating-point and integer types for individual elements. MX formats balance the competing needs of hardware efficiency, model accuracy, and user friction. Empirical results on over two dozen benchmarks demonstrate practicality of MX data formats as a drop-in replacement for baseline FP32 for AI inference and training with low user friction. We also show the first instance of training generative language models at sub-8-bit weights, activations, and gradients with minimal accuracy loss and no modifications to the training recipe.

Shared Microexponents: A Little Shifting Goes a Long Way

This paper introduces Block Data Representations (BDR), a framework for exploring and evaluating a wide spectrum of narrow-precision formats for deep learning. It enables comparison of popular quantization standards, and through BDR, new formats based on shared microexponents (MX) are identified, which outperform other state-of-the-art quantization approaches, including narrow-precision floating-point and block floating-point. MX utilizes multiple levels of quantization scaling with ultra-fine scaling factors based on shared microexponents in the hardware. The effectiveness of MX is demonstrated on real-world models including large-scale generative pretraining and inferencing, and production-scale recommendation systems.

Non-Local Feature Aggregation on Graphs via Latent Fixed Data Structures

In contrast to image/text data whose order can be used to perform non-local feature aggregation in a straightforward way using the pooling layers, graphs lack the tensor representation and mostly the element-wise max/mean function is utilized to aggregate the locally extracted feature vectors. In this paper, we present a novel approach for global feature aggregation in Graph Neural Networks (GNNs) which utilizes a Latent Fixed Data Structure (LFDS) to aggregate the extracted feature vectors. The locally extracted feature vectors are sorted/distributed on the LFDS and a latent neural network (CNN/GNN) is utilized to perform feature aggregation on the LFDS. The proposed approach is used to design several novel global feature aggregation methods based on the choice of the LFDS. We introduce multiple LFDSs including loop, 3D tensor (image), sequence, data driven graphs and an algorithm which sorts/distributes the extracted local feature vectors on the LFDS. While the computational complexity of the proposed methods are linear with the order of input graphs, they achieve competitive or better results.

Sampling and Reconstruction of Graph Signals via Weak Submodularity and Semidefinite Relaxation

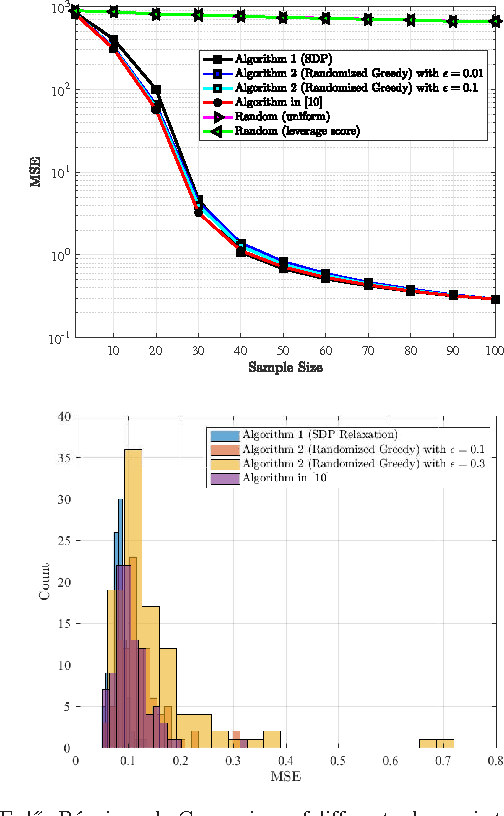
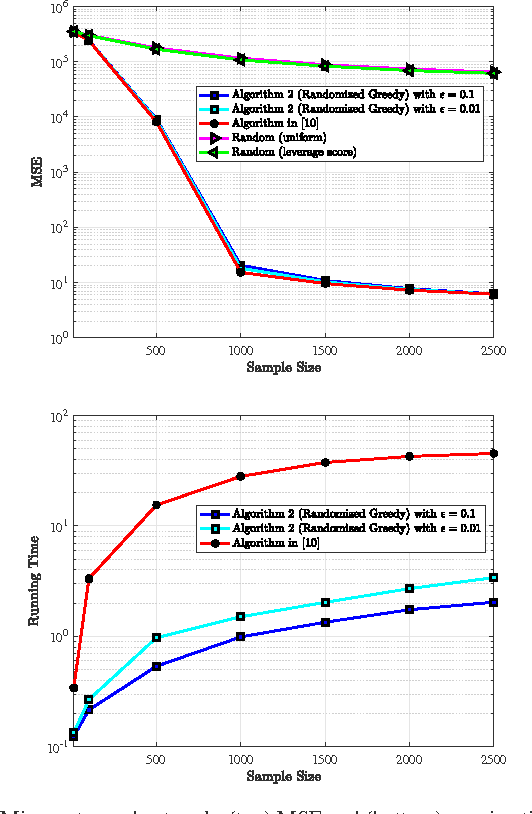
We study the problem of sampling a bandlimited graph signal in the presence of noise, where the objective is to select a node subset of prescribed cardinality that minimizes the signal reconstruction mean squared error (MSE). To that end, we formulate the task at hand as the minimization of MSE subject to binary constraints, and approximate the resulting NP-hard problem via semidefinite programming (SDP) relaxation. Moreover, we provide an alternative formulation based on maximizing a monotone weak submodular function and propose a randomized-greedy algorithm to find a sub-optimal subset. We then derive a worst-case performance guarantee on the MSE returned by the randomized greedy algorithm for general non-stationary graph signals. The efficacy of the proposed methods is illustrated through numerical simulations on synthetic and real-world graphs. Notably, the randomized greedy algorithm yields an order-of-magnitude speedup over state-of-the-art greedy sampling schemes, while incurring only a marginal MSE performance loss.