Sampling and Reconstruction of Graph Signals via Weak Submodularity and Semidefinite Relaxation
Paper and Code
Oct 31, 2017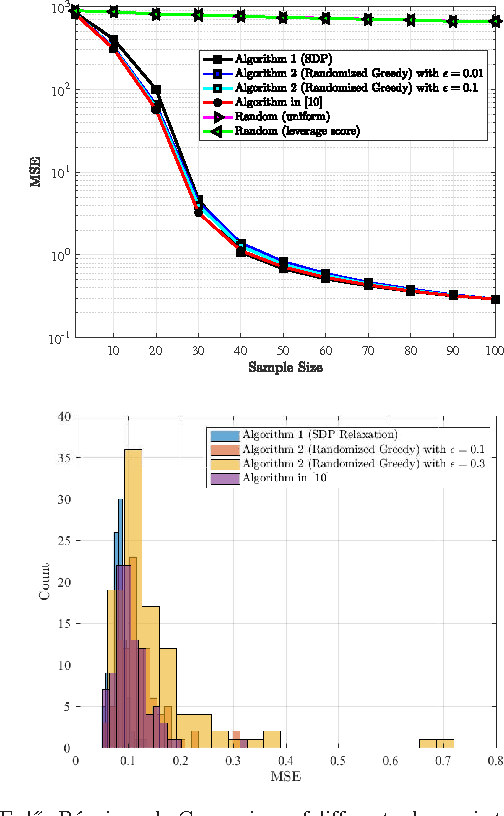
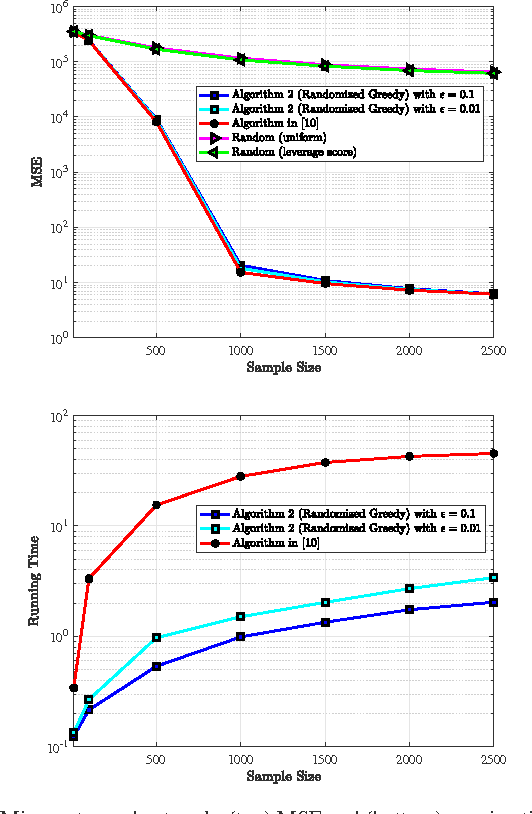
We study the problem of sampling a bandlimited graph signal in the presence of noise, where the objective is to select a node subset of prescribed cardinality that minimizes the signal reconstruction mean squared error (MSE). To that end, we formulate the task at hand as the minimization of MSE subject to binary constraints, and approximate the resulting NP-hard problem via semidefinite programming (SDP) relaxation. Moreover, we provide an alternative formulation based on maximizing a monotone weak submodular function and propose a randomized-greedy algorithm to find a sub-optimal subset. We then derive a worst-case performance guarantee on the MSE returned by the randomized greedy algorithm for general non-stationary graph signals. The efficacy of the proposed methods is illustrated through numerical simulations on synthetic and real-world graphs. Notably, the randomized greedy algorithm yields an order-of-magnitude speedup over state-of-the-art greedy sampling schemes, while incurring only a marginal MSE performance loss.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge