Towards Large Reasoning Models: A Survey on Scaling LLM Reasoning Capabilities

Language has long been conceived as an essential tool for human reasoning. The breakthrough of Large Language Models (LLMs) has sparked significant research interest in leveraging these models to tackle complex reasoning tasks. Researchers have moved beyond simple autoregressive token generation by introducing the concept of "thought" -- a sequence of tokens representing intermediate steps in the reasoning process. This innovative paradigm enables LLMs' to mimic complex human reasoning processes, such as tree search and reflective thinking. Recently, an emerging trend of learning to reason has applied reinforcement learning (RL) to train LLMs to master reasoning processes. This approach enables the automatic generation of high-quality reasoning trajectories through trial-and-error search algorithms, significantly expanding LLMs' reasoning capacity by providing substantially more training data. Furthermore, recent studies demonstrate that encouraging LLMs to "think" with more tokens during test-time inference can further significantly boost reasoning accuracy. Therefore, the train-time and test-time scaling combined to show a new research frontier -- a path toward Large Reasoning Model. The introduction of OpenAI's o1 series marks a significant milestone in this research direction. In this survey, we present a comprehensive review of recent progress in LLM reasoning. We begin by introducing the foundational background of LLMs and then explore the key technical components driving the development of large reasoning models, with a focus on automated data construction, learning-to-reason techniques, and test-time scaling. We also analyze popular open-source projects at building large reasoning models, and conclude with open challenges and future research directions.

Towards Large Reasoning Models: A Survey of Reinforced Reasoning with Large Language Models

Language has long been conceived as an essential tool for human reasoning. The breakthrough of Large Language Models (LLMs) has sparked significant research interest in leveraging these models to tackle complex reasoning tasks. Researchers have moved beyond simple autoregressive token generation by introducing the concept of "thought" -- a sequence of tokens representing intermediate steps in the reasoning process. This innovative paradigm enables LLMs' to mimic complex human reasoning processes, such as tree search and reflective thinking. Recently, an emerging trend of learning to reason has applied reinforcement learning (RL) to train LLMs to master reasoning processes. This approach enables the automatic generation of high-quality reasoning trajectories through trial-and-error search algorithms, significantly expanding LLMs' reasoning capacity by providing substantially more training data. Furthermore, recent studies demonstrate that encouraging LLMs to "think" with more tokens during test-time inference can further significantly boost reasoning accuracy. Therefore, the train-time and test-time scaling combined to show a new research frontier -- a path toward Large Reasoning Model. The introduction of OpenAI's o1 series marks a significant milestone in this research direction. In this survey, we present a comprehensive review of recent progress in LLM reasoning. We begin by introducing the foundational background of LLMs and then explore the key technical components driving the development of large reasoning models, with a focus on automated data construction, learning-to-reason techniques, and test-time scaling. We also analyze popular open-source projects at building large reasoning models, and conclude with open challenges and future research directions.

Perceive, Reflect, and Plan: Designing LLM Agent for Goal-Directed City Navigation without Instructions

This paper considers a scenario in city navigation: an AI agent is provided with language descriptions of the goal location with respect to some well-known landmarks; By only observing the scene around, including recognizing landmarks and road network connections, the agent has to make decisions to navigate to the goal location without instructions. This problem is very challenging, because it requires agent to establish self-position and acquire spatial representation of complex urban environment, where landmarks are often invisible. In the absence of navigation instructions, such abilities are vital for the agent to make high-quality decisions in long-range city navigation. With the emergent reasoning ability of large language models (LLMs), a tempting baseline is to prompt LLMs to "react" on each observation and make decisions accordingly. However, this baseline has very poor performance that the agent often repeatedly visits same locations and make short-sighted, inconsistent decisions. To address these issues, this paper introduces a novel agentic workflow featured by its abilities to perceive, reflect and plan. Specifically, we find LLaVA-7B can be fine-tuned to perceive the direction and distance of landmarks with sufficient accuracy for city navigation. Moreover, reflection is achieved through a memory mechanism, where past experiences are stored and can be retrieved with current perception for effective decision argumentation. Planning uses reflection results to produce long-term plans, which can avoid short-sighted decisions in long-range navigation. We show the designed workflow significantly improves navigation ability of the LLM agent compared with the state-of-the-art baselines.

Large scale analysis of generalization error in learning using margin based classification methods

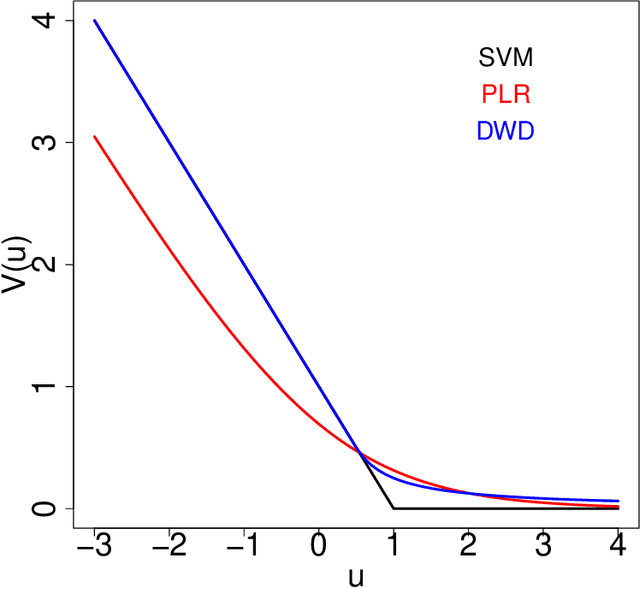
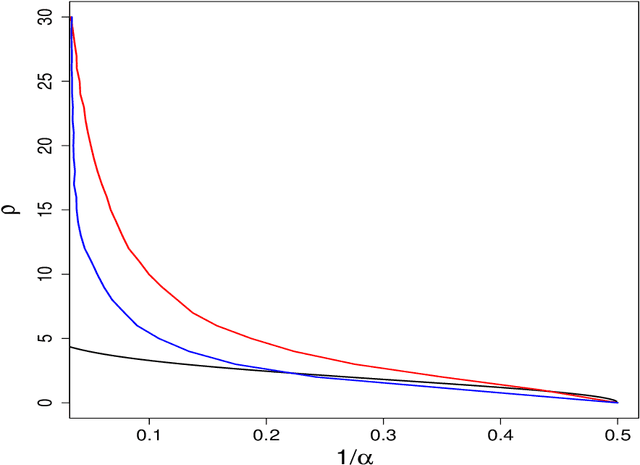
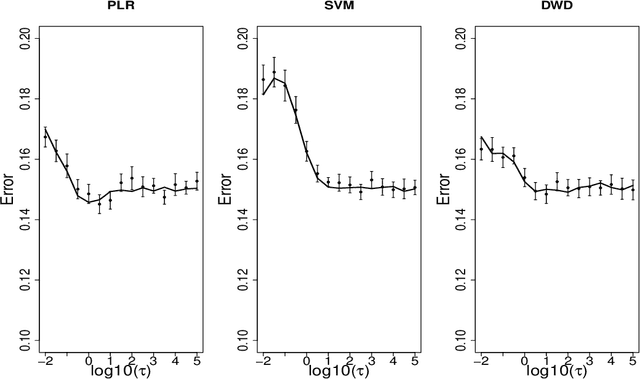
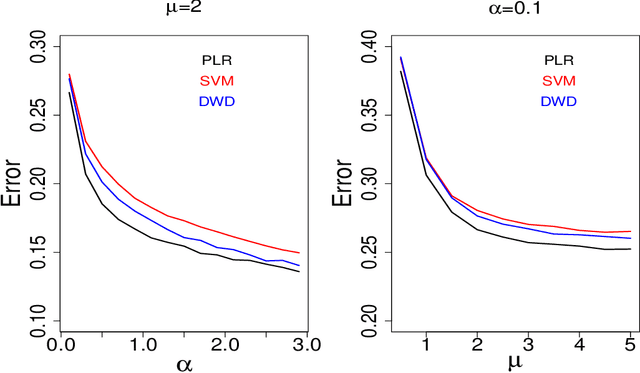
Large-margin classifiers are popular methods for classification. We derive the asymptotic expression for the generalization error of a family of large-margin classifiers in the limit of both sample size $n$ and dimension $p$ going to $\infty$ with fixed ratio $\alpha=n/p$. This family covers a broad range of commonly used classifiers including support vector machine, distance weighted discrimination, and penalized logistic regression. Our result can be used to establish the phase transition boundary for the separability of two classes. We assume that the data are generated from a single multivariate Gaussian distribution with arbitrary covariance structure. We explore two special choices for the covariance matrix: spiked population model and two layer neural networks with random first layer weights. The method we used for deriving the closed-form expression is from statistical physics known as the replica method. Our asymptotic results match simulations already when $n,p$ are of the order of a few hundreds. For two layer neural networks, we reproduce the recently developed `double descent' phenomenology for several classification models. We also discuss some statistical insights that can be drawn from these analysis.

SNAP: A semismooth Newton algorithm for pathwise optimization with optimal local convergence rate and oracle properties

We propose a semismooth Newton algorithm for pathwise optimization (SNAP) for the LASSO and Enet in sparse, high-dimensional linear regression. SNAP is derived from a suitable formulation of the KKT conditions based on Newton derivatives. It solves the semismooth KKT equations efficiently by actively and continuously seeking the support of the regression coefficients along the solution path with warm start. At each knot in the path, SNAP converges locally superlinearly for the Enet criterion and achieves an optimal local convergence rate for the LASSO criterion, i.e., SNAP converges in one step at the cost of two matrix-vector multiplication per iteration. Under certain regularity conditions on the design matrix and the minimum magnitude of the nonzero elements of the target regression coefficients, we show that SNAP hits a solution with the same signs as the regression coefficients and achieves a sharp estimation error bound in finite steps with high probability. The computational complexity of SNAP is shown to be the same as that of LARS and coordinate descent algorithms per iteration. Simulation studies and real data analysis support our theoretical results and demonstrate that SNAP is faster and accurate than LARS and coordinate descent algorithms.