A Closed-Form Framework for Schrödinger Bridges Between Arbitrary Densities

Score-based generative models have recently attracted significant attention for their ability to generate high-fidelity data by learning maps from simple Gaussian priors to complex data distributions. A natural generalization of this idea to transformations between arbitrary probability distributions leads to the Schrödinger Bridge (SB) problem. However, SB solutions rarely admit closed-form expressios and are commonly obtained through iterative stochastic simulation procedures, which are computationally intensive and can be unstable. In this work, we introduce a unified closed-form framework for representing the stochastic dynamics of SB systems. Our formulation subsumes previously known analytical solutions including the Schrödinger Föllmer process and the Gaussian SB as specific instances. Notably, the classical Gaussian SB solution, previously derived using substantially more sophisticated tools such as Riemannian geometry and generator theory, follows directly from our formulation as an immediate corollary. Leveraging this framework, we develop a simulation-free algorithm that infers SB dynamics directly from samples of the source and target distributions. We demonstrate the versatility of our approach in two settings: (i) modeling developmental trajectories in single-cell genomics and (ii) solving image restoration tasks such as inpainting and deblurring. This work opens a new direction for efficient and scalable nonlinear diffusion modeling across scientific and machine learning applications.

Statistical Inference in Classification of High-dimensional Gaussian Mixture

We consider the classification problem of a high-dimensional mixture of two Gaussians with general covariance matrices. Using the replica method from statistical physics, we investigate the asymptotic behavior of a general class of regularized convex classifiers in the high-dimensional limit, where both the sample size $n$ and the dimension $p$ approach infinity while their ratio $\alpha=n/p$ remains fixed. Our focus is on the generalization error and variable selection properties of the estimators. Specifically, based on the distributional limit of the classifier, we construct a de-biased estimator to perform variable selection through an appropriate hypothesis testing procedure. Using $L_1$-regularized logistic regression as an example, we conducted extensive computational experiments to confirm that our analytical findings are consistent with numerical simulations in finite-sized systems. We also explore the influence of the covariance structure on the performance of the de-biased estimator.

Schrödinger bridge based deep conditional generative learning

Conditional generative models represent a significant advancement in the field of machine learning, allowing for the controlled synthesis of data by incorporating additional information into the generation process. In this work we introduce a novel Schr\"odinger bridge based deep generative method for learning conditional distributions. We start from a unit-time diffusion process governed by a stochastic differential equation (SDE) that transforms a fixed point at time $0$ into a desired target conditional distribution at time $1$. For effective implementation, we discretize the SDE with Euler-Maruyama method where we estimate the drift term nonparametrically using a deep neural network. We apply our method to both low-dimensional and high-dimensional conditional generation problems. The numerical studies demonstrate that though our method does not directly provide the conditional density estimation, the samples generated by this method exhibit higher quality compared to those obtained by several existing methods. Moreover, the generated samples can be effectively utilized to estimate the conditional density and related statistical quantities, such as conditional mean and conditional standard deviation.

Large scale analysis of generalization error in learning using margin based classification methods

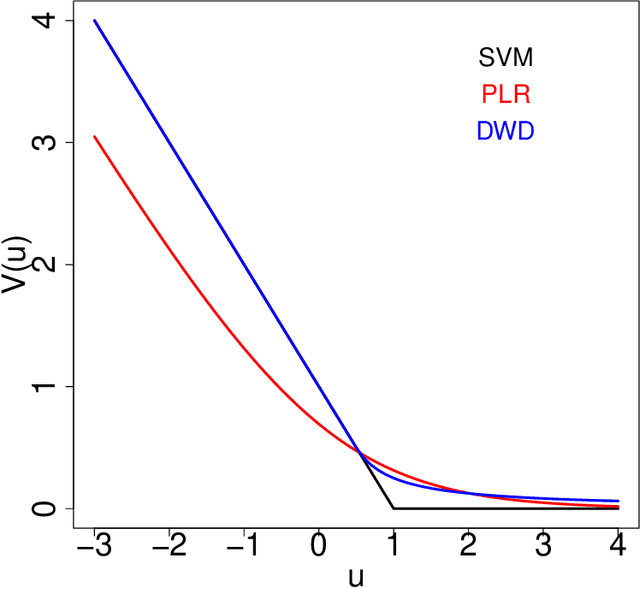
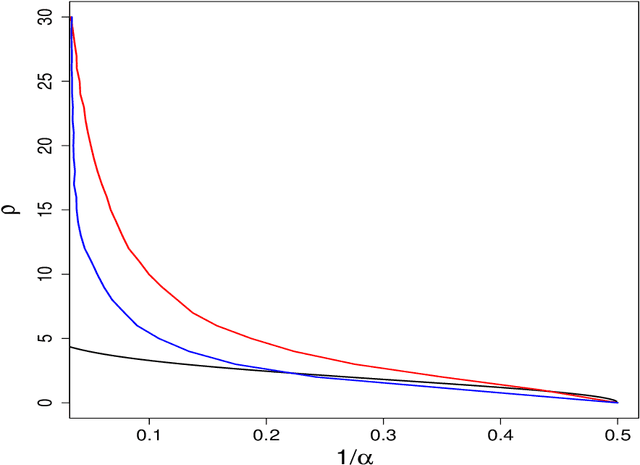
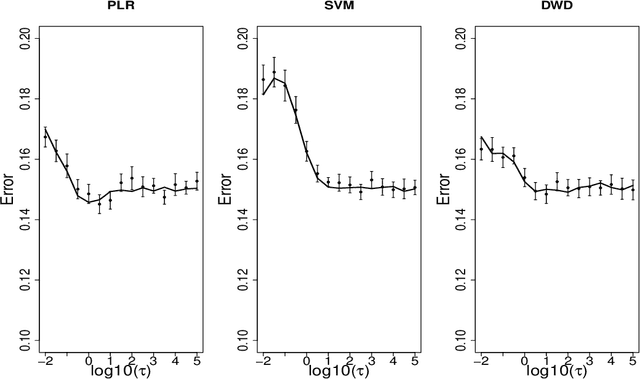
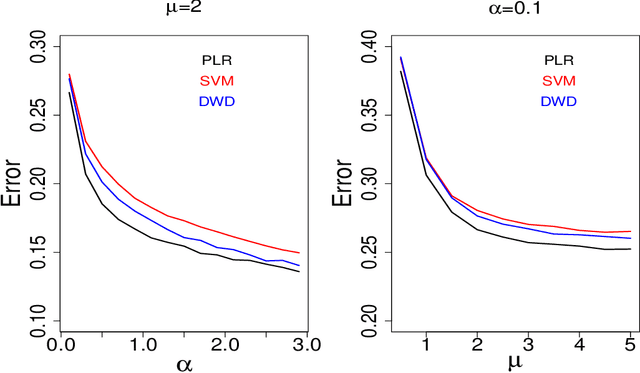
Large-margin classifiers are popular methods for classification. We derive the asymptotic expression for the generalization error of a family of large-margin classifiers in the limit of both sample size $n$ and dimension $p$ going to $\infty$ with fixed ratio $\alpha=n/p$. This family covers a broad range of commonly used classifiers including support vector machine, distance weighted discrimination, and penalized logistic regression. Our result can be used to establish the phase transition boundary for the separability of two classes. We assume that the data are generated from a single multivariate Gaussian distribution with arbitrary covariance structure. We explore two special choices for the covariance matrix: spiked population model and two layer neural networks with random first layer weights. The method we used for deriving the closed-form expression is from statistical physics known as the replica method. Our asymptotic results match simulations already when $n,p$ are of the order of a few hundreds. For two layer neural networks, we reproduce the recently developed `double descent' phenomenology for several classification models. We also discuss some statistical insights that can be drawn from these analysis.

Large dimensional analysis of general margin based classification methods

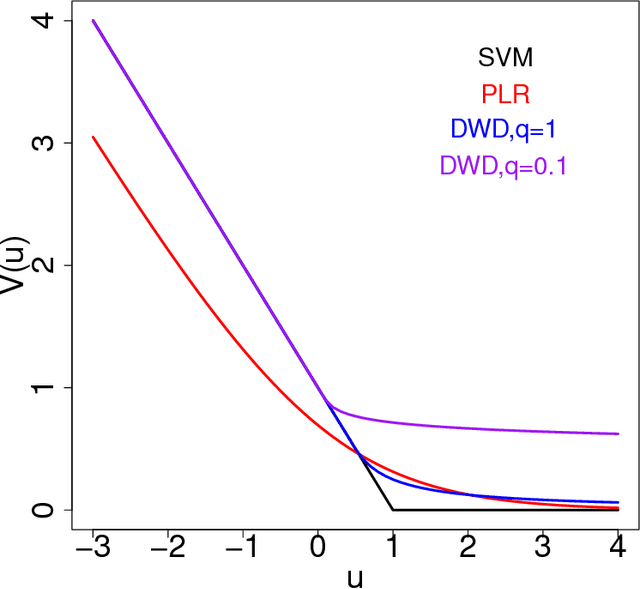
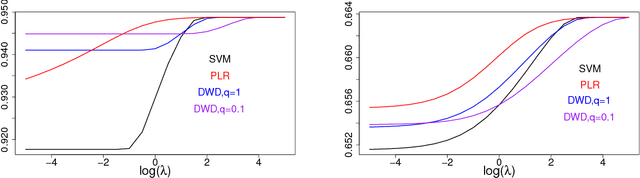
Margin-based classifiers have been popular in both machine learning and statistics for classification problems. Since a large number of classifiers are available, one natural question is which type of classifiers should be used given a particular classification task. We aim to answering this question by investigating the asymptotic performance of a family of large-margin classifiers in situations where the data dimension $p$ and the sample $n$ are both large. This family covers a broad range of classifiers including support vector machine, distance weighted discrimination, penalized logistic regression, and large-margin unified machine as special cases. The asymptotic results are described by a set of nonlinear equations and we observe a close match of them with Monte Carlo simulation on finite data samples. Our analytical studies shed new light on how to select the best classifier among various classification methods as well as on how to choose the optimal tuning parameters for a given method.