Quantifying Feature Contributions to Overall Disparity Using Information Theory

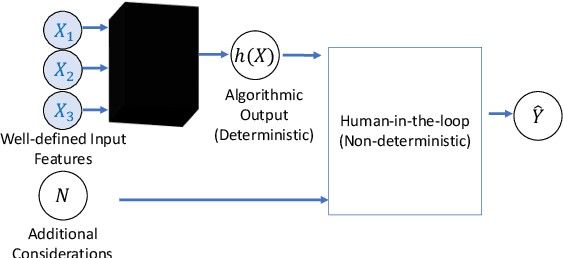
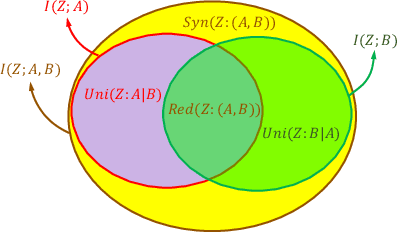
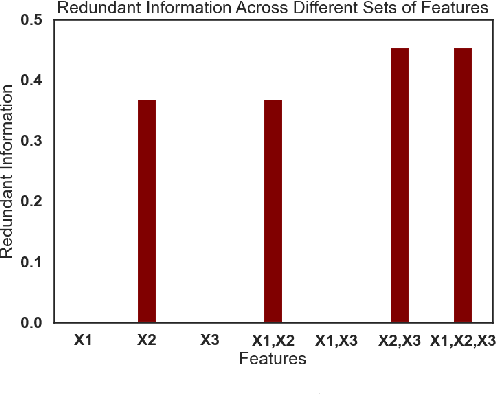
When a machine-learning algorithm makes biased decisions, it can be helpful to understand the sources of disparity to explain why the bias exists. Towards this, we examine the problem of quantifying the contribution of each individual feature to the observed disparity. If we have access to the decision-making model, one potential approach (inspired from intervention-based approaches in explainability literature) is to vary each individual feature (while keeping the others fixed) and use the resulting change in disparity to quantify its contribution. However, we may not have access to the model or be able to test/audit its outputs for individually varying features. Furthermore, the decision may not always be a deterministic function of the input features (e.g., with human-in-the-loop). For these situations, we might need to explain contributions using purely distributional (i.e., observational) techniques, rather than interventional. We ask the question: what is the "potential" contribution of each individual feature to the observed disparity in the decisions when the exact decision-making mechanism is not accessible? We first provide canonical examples (thought experiments) that help illustrate the difference between distributional and interventional approaches to explaining contributions, and when either is better suited. When unable to intervene on the inputs, we quantify the "redundant" statistical dependency about the protected attribute that is present in both the final decision and an individual feature, by leveraging a body of work in information theory called Partial Information Decomposition. We also perform a simple case study to show how this technique could be applied to quantify contributions.

Fast and Real-time End to End Control in Autonomous Racing Cars Through Representation Learning

The challenges presented in an autonomous racing situation are distinct from those faced in regular autonomous driving and require faster end-to-end algorithms and consideration of a longer horizon in determining optimal current actions keeping in mind upcoming maneuvers and situations. In this paper, we propose an end-to-end method for autonomous racing that takes in as inputs video information from an onboard camera and determines final steering and throttle control actions. We use the following split to construct such a method (1) learning a low dimensional representation of the scene, (2) pre-generating the optimal trajectory for the given scene, and (3) tracking the predicted trajectory using a classical control method. In learning a low-dimensional representation of the scene, we use intermediate representations with a novel unsupervised trajectory planner to generate expert trajectories, and hence utilize them to directly predict race lines from a given front-facing input image. Thus, the proposed algorithm employs the best of two worlds - the robustness of learning-based approaches to perception and the accuracy of optimization-based approaches for trajectory generation in an end-to-end learning-based framework. We deploy and demonstrate our framework on CARLA, a photorealistic simulator for testing self-driving cars in realistic environments.

Learning by Cheating : An End-to-End Zero Shot Framework for Autonomous Drone Navigation

This paper proposes a novel framework for autonomous drone navigation through a cluttered environment. Control policies are learnt in a low-level environment during training and are applied to a complex environment during inference. The controller learnt in the training environment is tricked into believing that the robot is still in the training environment when it is actually navigating in a more complex environment. The framework presented in this paper can be adapted to reuse simple policies in more complex tasks. We also show that the framework can be used as an interpretation tool for reinforcement learning algorithms.

Can Information Flows Suggest Targets for Interventions in Neural Circuits?

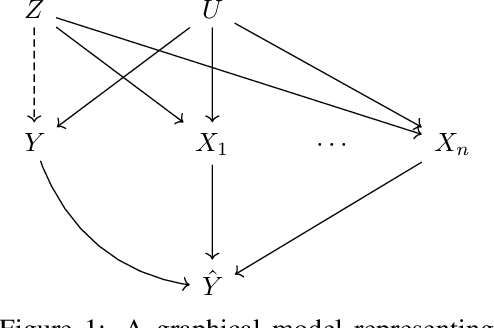
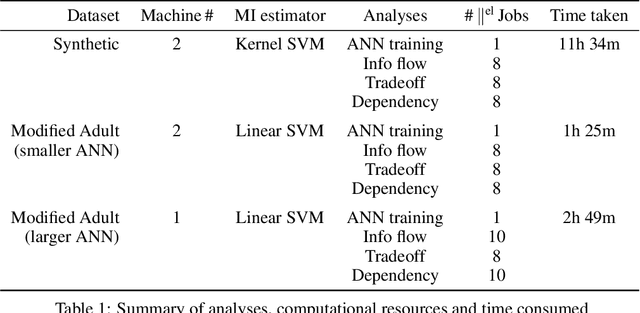
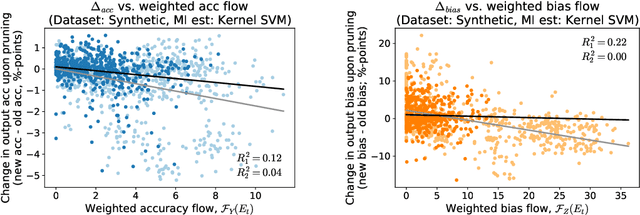
Motivated by neuroscientific and clinical applications, we empirically examine whether observational measures of information flow can suggest interventions. We do so by performing experiments on artificial neural networks in the context of fairness in machine learning, where the goal is to induce fairness in the system through interventions. Using our recently developed $M$-information flow framework, we measure the flow of information about the true label (responsible for accuracy, and hence desirable), and separately, the flow of information about a protected attribute (responsible for bias, and hence undesirable) on the edges of a trained neural network. We then compare the flow magnitudes against the effect of intervening on those edges by pruning. We show that pruning edges that carry larger information flows about the protected attribute reduces bias at the output to a greater extent. This demonstrates that $M$-information flow can meaningfully suggest targets for interventions, answering the title's question in the affirmative. We also evaluate bias-accuracy tradeoffs for different intervention strategies, to analyze how one might use estimates of desirable and undesirable information flows (here, accuracy and bias flows) to inform interventions that preserve the former while reducing the latter.

Memory Guided Road Detection

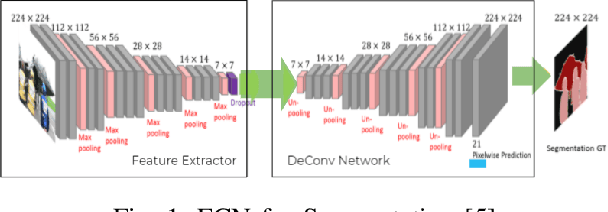
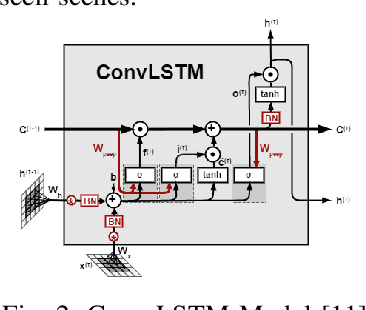
In self driving car applications, there is a requirement to predict the location of the lane given an input RGB front facing image. In this paper, we propose an architecture that allows us to increase the speed and robustness of road detection without a large hit in accuracy by introducing an underlying shared feature space that is propagated over time, which serves as a flowing dynamic memory. By utilizing the gist of previous frames, we train the network to predict the current road with a greater accuracy and lesser deviation from previous frames.

Fairness Under Feature Exemptions: Counterfactual and Observational Measures

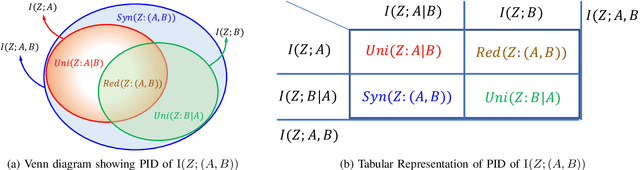
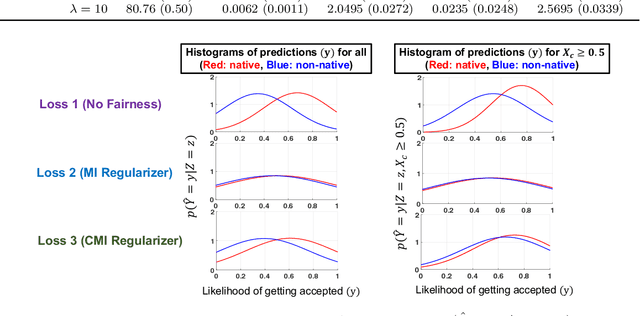
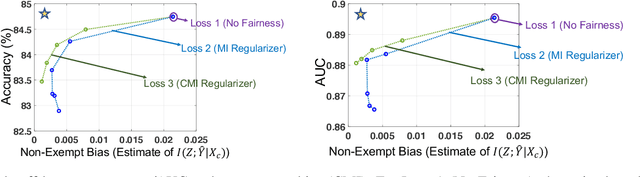
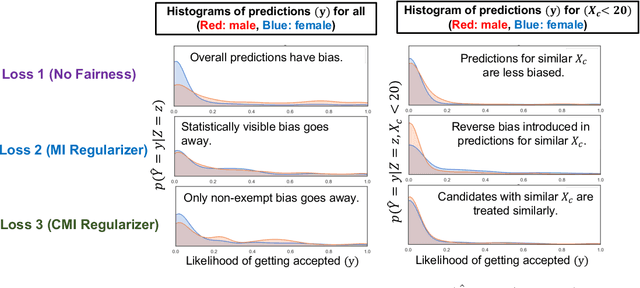
With the growing use of AI in highly consequential domains, the quantification and removal of bias with respect to protected attributes, such as gender, race, etc., is becoming increasingly important. While quantifying bias is essential, sometimes the needs of a business (e.g., hiring) may require the use of certain features that are critical in a way that any bias that can be explained by them might need to be exempted. E.g., a standardized test-score may be a critical feature that should be weighed strongly in hiring even if biased, whereas other features, such as zip code may be used only to the extent that they do not discriminate. In this work, we propose a novel information-theoretic decomposition of the total bias (in a counterfactual sense) into a non-exempt component that quantifies the part of the bias that cannot be accounted for by the critical features, and an exempt component which quantifies the remaining bias. This decomposition allows one to check if the bias arose purely due to the critical features (inspired from the business necessity defense of disparate impact law) and also enables selective removal of the non-exempt component if desired. We arrive at this decomposition through examples that lead to a set of desirable properties (axioms) that any measure of non-exempt bias should satisfy. We demonstrate that our proposed counterfactual measure satisfies all of them. Our quantification bridges ideas of causality, Simpson's paradox, and a body of work from information theory called Partial Information Decomposition. We also obtain an impossibility result showing that no observational measure of non-exempt bias can satisfy all of the desirable properties, which leads us to relax our goals and examine observational measures that satisfy only some of these properties. We then perform case studies to show how one can train models while reducing non-exempt bias.

Testing Changes in Communities for the Stochastic Block Model

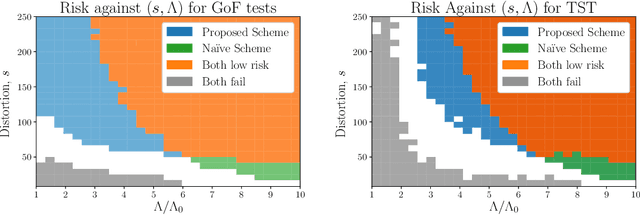
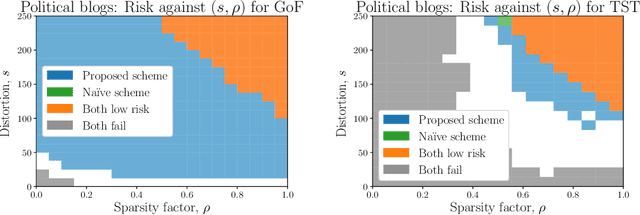
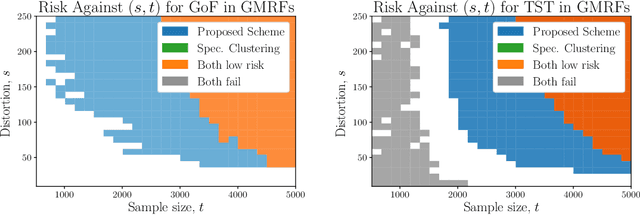
We introduce the problems of goodness-of-fit and two-sample testing of the latent community structure in a 2-community, symmetric, stochastic block model (SBM), in the regime where recovery of the structure is difficult. The latter problem may be described as follows: let $x,y$ be two latent community partitions. Given graphs $G,H$ drawn according to SBMs with partitions $x,y$, respectively, we wish to test the hypothesis $x = y$ against $d(x,y) \ge s,$ for a given Hamming distortion parameter $s \ll n$. Prior work showed that `partial' recovery of these partitions up to distortion $s$ with vanishing error probability requires that the signal-to-noise ratio $(\mathrm{SNR})$ is $\gtrsim C \log (n/s).$ We prove by constructing simple schemes that if $s \gg \sqrt{n \log n},$ then these testing problems can be solved even if $\mathrm{SNR} = O(1).$ For $s = o(\sqrt{n}),$ and constant order degrees, we show via an information-theoretic lower bound that both testing problems require $\mathrm{SNR} = \Omega(\log(n)),$ and thus at this scale the na\"{i}ve scheme of learning the communities and comparing them is minimax optimal up to constant factors. These results are augmented by simulations of goodness-of-fit and two-sample testing for standard SBMs as well as for Gaussian Markov random fields with underlying SBM structure.