Time-varying EEG spectral power predicts evoked and spontaneous fMRI motor brain activity

Simultaneous EEG-fMRI recordings are increasingly used to investigate brain activity by leveraging the complementary high spatial and high temporal resolution of fMRI and EEG signals respectively. It remains unclear, however, to what degree these two imaging modalities capture shared information about neural activity. Here, we investigate whether it is possible to predict both task-evoked and spontaneous fMRI signals of motor brain networks from EEG time-varying spectral power using interpretable models trained for individual subjects with Sparse Group Lasso regularization. Critically, we test the trained models on data acquired from each subject on a different day and obtain statistical validation by comparison with appropriate null models as well as the conventional EEG sensorimotor rhythm. We find significant prediction results in most subjects, although less frequently for resting-state compared to task-based conditions. Furthermore, we interpret the model learned parameters to understand representations of EEG-fMRI coupling in terms of predictive EEG channels, frequencies, and haemodynamic delays. In conclusion, our work provides evidence of the ability to predict fMRI motor brain activity from EEG recordings alone across different days, in both task-evoked and spontaneous conditions, with statistical significance in individual subjects. These results present great potential for translation to EEG neurofeedback applications.

Quantifying Feature Contributions to Overall Disparity Using Information Theory

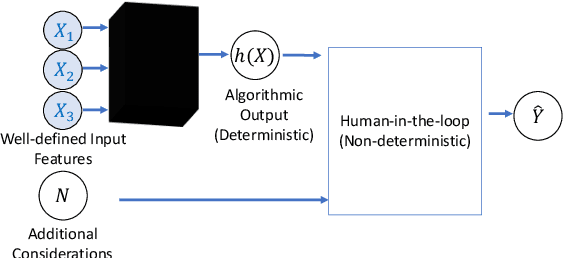
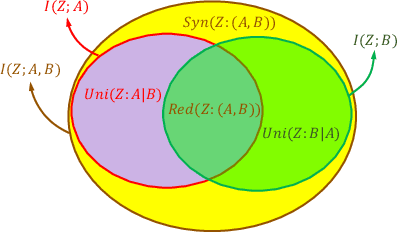
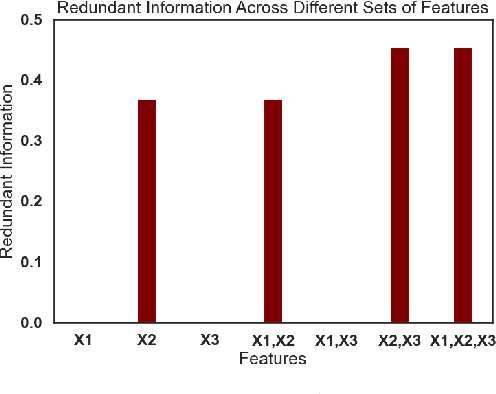
When a machine-learning algorithm makes biased decisions, it can be helpful to understand the sources of disparity to explain why the bias exists. Towards this, we examine the problem of quantifying the contribution of each individual feature to the observed disparity. If we have access to the decision-making model, one potential approach (inspired from intervention-based approaches in explainability literature) is to vary each individual feature (while keeping the others fixed) and use the resulting change in disparity to quantify its contribution. However, we may not have access to the model or be able to test/audit its outputs for individually varying features. Furthermore, the decision may not always be a deterministic function of the input features (e.g., with human-in-the-loop). For these situations, we might need to explain contributions using purely distributional (i.e., observational) techniques, rather than interventional. We ask the question: what is the "potential" contribution of each individual feature to the observed disparity in the decisions when the exact decision-making mechanism is not accessible? We first provide canonical examples (thought experiments) that help illustrate the difference between distributional and interventional approaches to explaining contributions, and when either is better suited. When unable to intervene on the inputs, we quantify the "redundant" statistical dependency about the protected attribute that is present in both the final decision and an individual feature, by leveraging a body of work in information theory called Partial Information Decomposition. We also perform a simple case study to show how this technique could be applied to quantify contributions.

Can Information Flows Suggest Targets for Interventions in Neural Circuits?

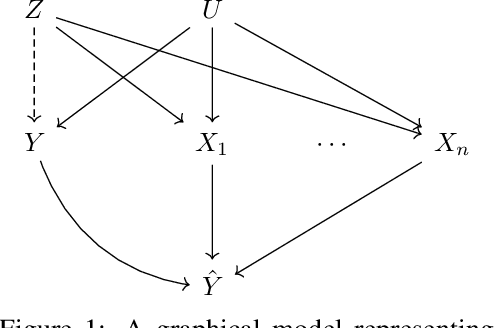
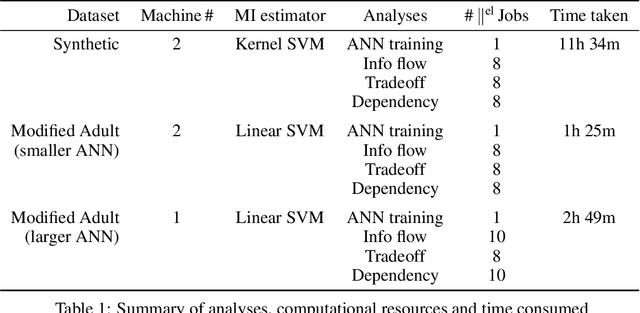
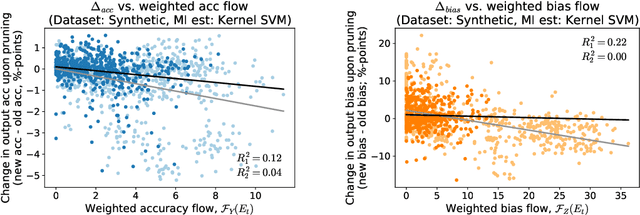
Motivated by neuroscientific and clinical applications, we empirically examine whether observational measures of information flow can suggest interventions. We do so by performing experiments on artificial neural networks in the context of fairness in machine learning, where the goal is to induce fairness in the system through interventions. Using our recently developed $M$-information flow framework, we measure the flow of information about the true label (responsible for accuracy, and hence desirable), and separately, the flow of information about a protected attribute (responsible for bias, and hence undesirable) on the edges of a trained neural network. We then compare the flow magnitudes against the effect of intervening on those edges by pruning. We show that pruning edges that carry larger information flows about the protected attribute reduces bias at the output to a greater extent. This demonstrates that $M$-information flow can meaningfully suggest targets for interventions, answering the title's question in the affirmative. We also evaluate bias-accuracy tradeoffs for different intervention strategies, to analyze how one might use estimates of desirable and undesirable information flows (here, accuracy and bias flows) to inform interventions that preserve the former while reducing the latter.

Fairness Under Feature Exemptions: Counterfactual and Observational Measures

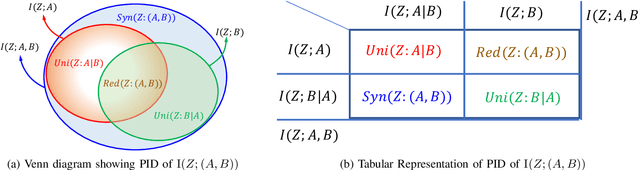
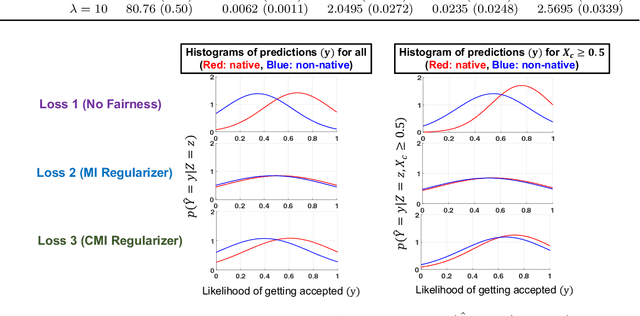
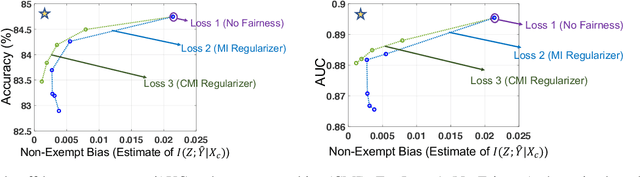
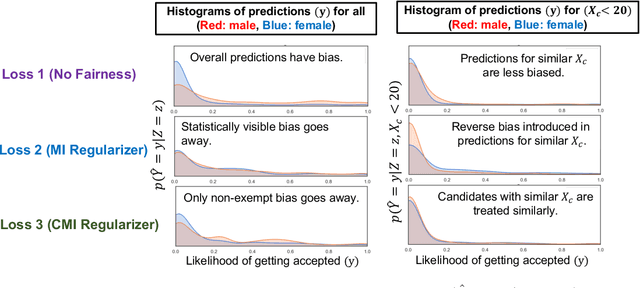
With the growing use of AI in highly consequential domains, the quantification and removal of bias with respect to protected attributes, such as gender, race, etc., is becoming increasingly important. While quantifying bias is essential, sometimes the needs of a business (e.g., hiring) may require the use of certain features that are critical in a way that any bias that can be explained by them might need to be exempted. E.g., a standardized test-score may be a critical feature that should be weighed strongly in hiring even if biased, whereas other features, such as zip code may be used only to the extent that they do not discriminate. In this work, we propose a novel information-theoretic decomposition of the total bias (in a counterfactual sense) into a non-exempt component that quantifies the part of the bias that cannot be accounted for by the critical features, and an exempt component which quantifies the remaining bias. This decomposition allows one to check if the bias arose purely due to the critical features (inspired from the business necessity defense of disparate impact law) and also enables selective removal of the non-exempt component if desired. We arrive at this decomposition through examples that lead to a set of desirable properties (axioms) that any measure of non-exempt bias should satisfy. We demonstrate that our proposed counterfactual measure satisfies all of them. Our quantification bridges ideas of causality, Simpson's paradox, and a body of work from information theory called Partial Information Decomposition. We also obtain an impossibility result showing that no observational measure of non-exempt bias can satisfy all of the desirable properties, which leads us to relax our goals and examine observational measures that satisfy only some of these properties. We then perform case studies to show how one can train models while reducing non-exempt bias.

CodeNet: Training Large Scale Neural Networks in Presence of Soft-Errors

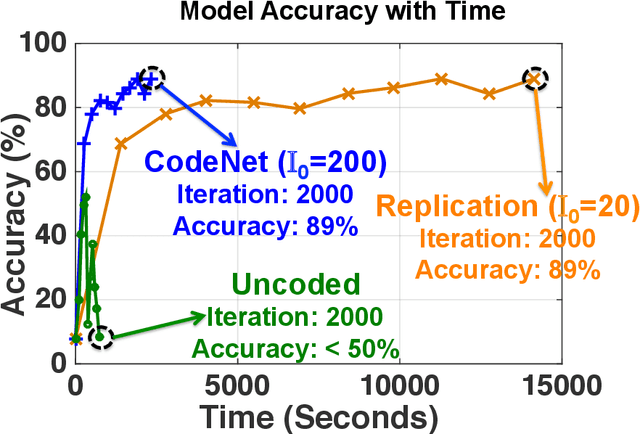
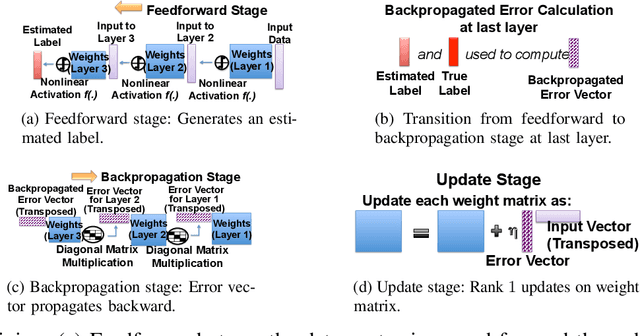
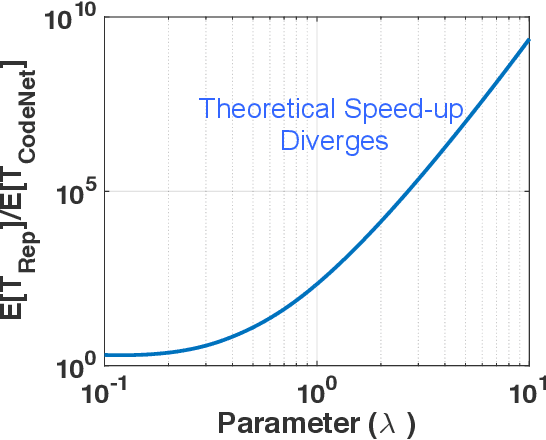
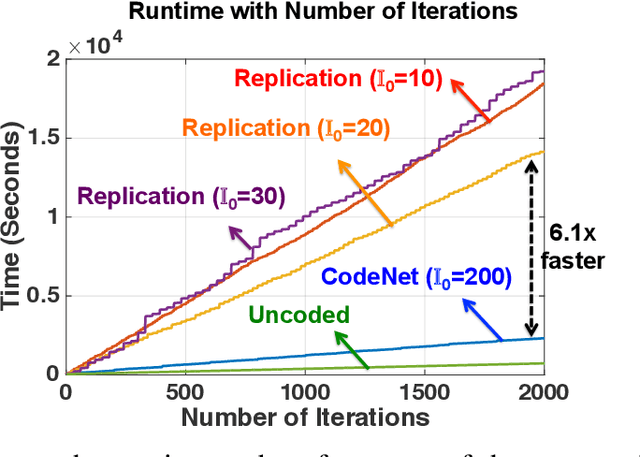
This work proposes the first strategy to make distributed training of neural networks resilient to computing errors, a problem that has remained unsolved despite being first posed in 1956 by von Neumann. He also speculated that the efficiency and reliability of the human brain is obtained by allowing for low power but error-prone components with redundancy for error-resilience. It is surprising that this problem remains open, even as massive artificial neural networks are being trained on increasingly low-cost and unreliable processing units. Our coding-theory-inspired strategy, "CodeNet," solves this problem by addressing three challenges in the science of reliable computing: (i) Providing the first strategy for error-resilient neural network training by encoding each layer separately; (ii) Keeping the overheads of coding (encoding/error-detection/decoding) low by obviating the need to re-encode the updated parameter matrices after each iteration from scratch. (iii) Providing a completely decentralized implementation with no central node (which is a single point of failure), allowing all primary computational steps to be error-prone. We theoretically demonstrate that CodeNet has higher error tolerance than replication, which we leverage to speed up computation time. Simultaneously, CodeNet requires lower redundancy than replication, and equal computational and communication costs in scaling sense. We first demonstrate the benefits of CodeNet in reducing expected computation time over replication when accounting for checkpointing. Our experiments show that CodeNet achieves the best accuracy-runtime tradeoff compared to both replication and uncoded strategies. CodeNet is a significant step towards biologically plausible neural network training, that could hold the key to orders of magnitude efficiency improvements.

A Unified Coded Deep Neural Network Training Strategy Based on Generalized PolyDot Codes for Matrix Multiplication

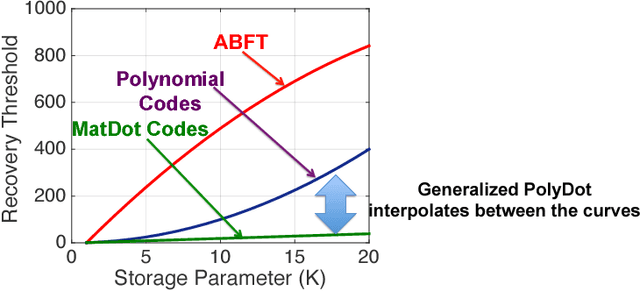
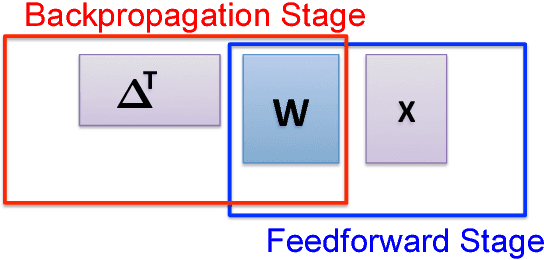
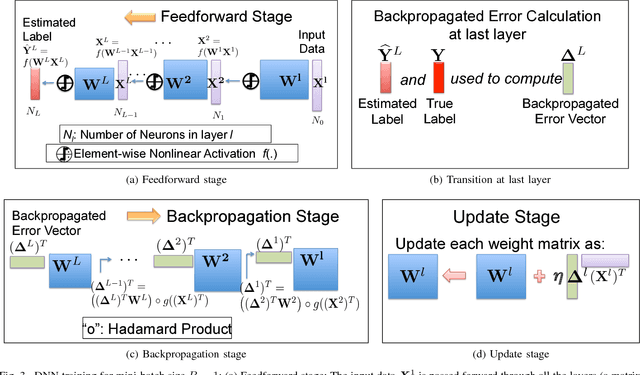
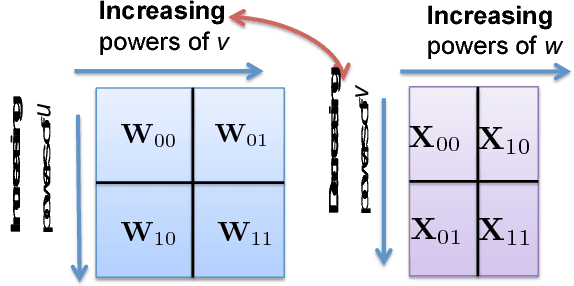
This paper has two contributions. First, we propose a novel coded matrix multiplication technique called Generalized PolyDot codes that advances on existing methods for coded matrix multiplication under storage and communication constraints. This technique uses "garbage alignment," i.e., aligning computations in coded computing that are not a part of the desired output. Generalized PolyDot codes bridge between Polynomial codes and MatDot codes, trading off between recovery threshold and communication costs. Second, we demonstrate that Generalized PolyDot can be used for training large Deep Neural Networks (DNNs) on unreliable nodes prone to soft-errors. This requires us to address three additional challenges: (i) prohibitively large overhead of coding the weight matrices in each layer of the DNN at each iteration; (ii) nonlinear operations during training, which are incompatible with linear coding; and (iii) not assuming presence of an error-free master node, requiring us to architect a fully decentralized implementation without any "single point of failure." We allow all primary DNN training steps, namely, matrix multiplication, nonlinear activation, Hadamard product, and update steps as well as the encoding/decoding to be error-prone. We consider the case of mini-batch size $B=1$, as well as $B>1$, leveraging coded matrix-vector products, and matrix-matrix products respectively. The problem of DNN training under soft-errors also motivates an interesting, probabilistic error model under which a real number $(P,Q)$ MDS code is shown to correct $P-Q-1$ errors with probability $1$ as compared to $\lfloor \frac{P-Q}{2} \rfloor$ for the more conventional, adversarial error model. We also demonstrate that our proposed strategy can provide unbounded gains in error tolerance over a competing replication strategy and a preliminary MDS-code-based strategy for both these error models.