CodeNet: Training Large Scale Neural Networks in Presence of Soft-Errors

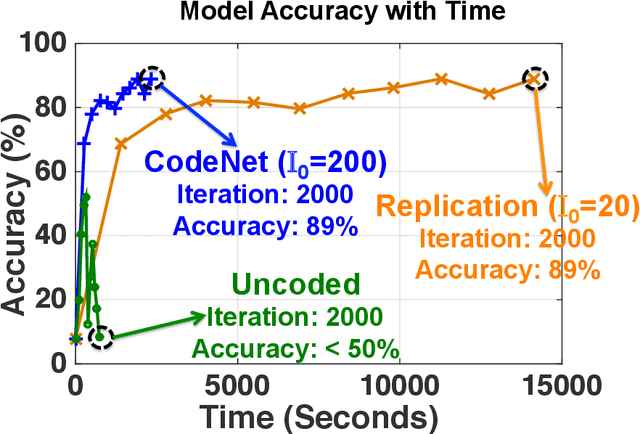
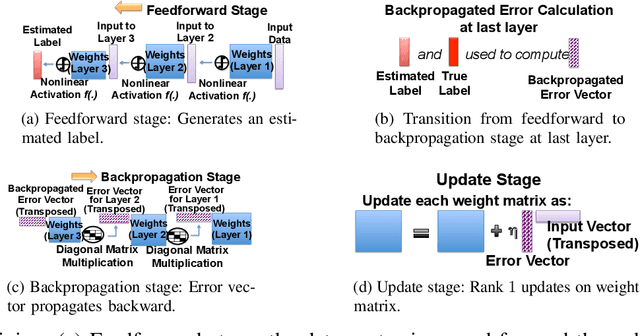
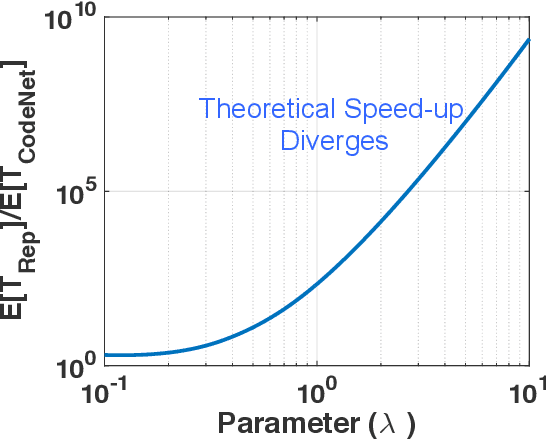
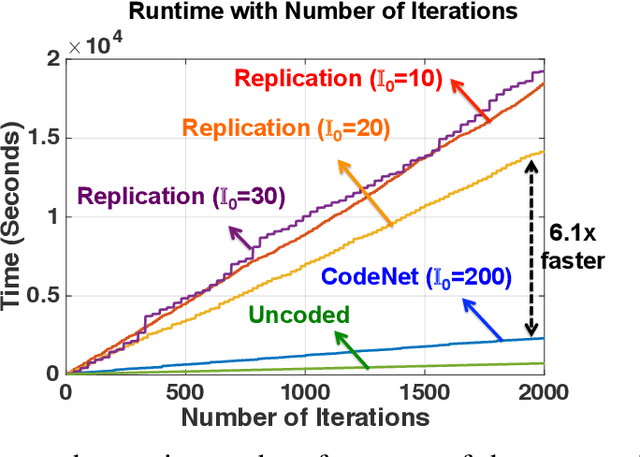
This work proposes the first strategy to make distributed training of neural networks resilient to computing errors, a problem that has remained unsolved despite being first posed in 1956 by von Neumann. He also speculated that the efficiency and reliability of the human brain is obtained by allowing for low power but error-prone components with redundancy for error-resilience. It is surprising that this problem remains open, even as massive artificial neural networks are being trained on increasingly low-cost and unreliable processing units. Our coding-theory-inspired strategy, "CodeNet," solves this problem by addressing three challenges in the science of reliable computing: (i) Providing the first strategy for error-resilient neural network training by encoding each layer separately; (ii) Keeping the overheads of coding (encoding/error-detection/decoding) low by obviating the need to re-encode the updated parameter matrices after each iteration from scratch. (iii) Providing a completely decentralized implementation with no central node (which is a single point of failure), allowing all primary computational steps to be error-prone. We theoretically demonstrate that CodeNet has higher error tolerance than replication, which we leverage to speed up computation time. Simultaneously, CodeNet requires lower redundancy than replication, and equal computational and communication costs in scaling sense. We first demonstrate the benefits of CodeNet in reducing expected computation time over replication when accounting for checkpointing. Our experiments show that CodeNet achieves the best accuracy-runtime tradeoff compared to both replication and uncoded strategies. CodeNet is a significant step towards biologically plausible neural network training, that could hold the key to orders of magnitude efficiency improvements.

A Unified Coded Deep Neural Network Training Strategy Based on Generalized PolyDot Codes for Matrix Multiplication

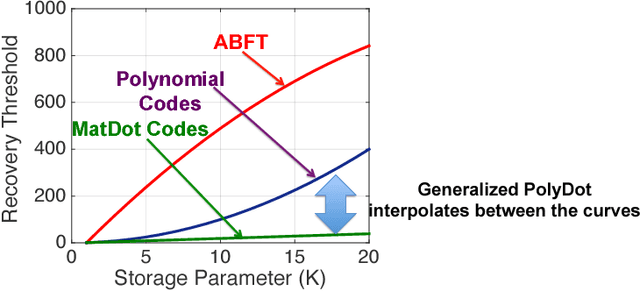
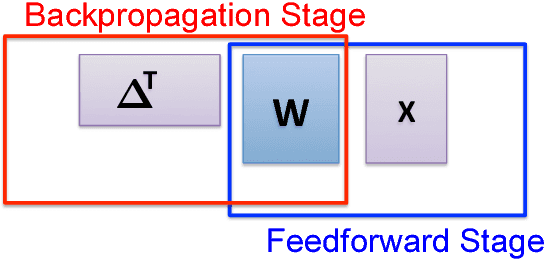
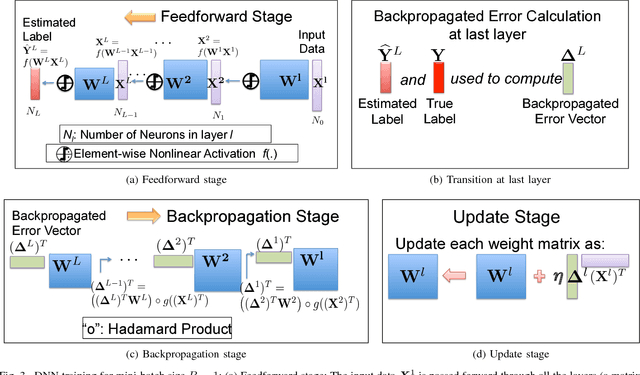
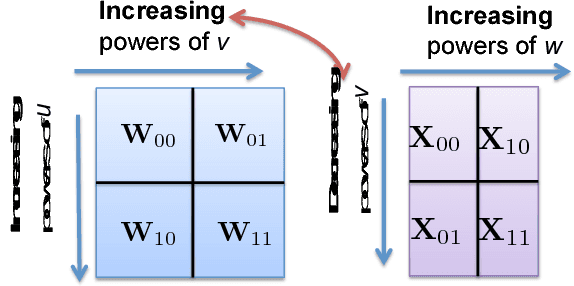
This paper has two contributions. First, we propose a novel coded matrix multiplication technique called Generalized PolyDot codes that advances on existing methods for coded matrix multiplication under storage and communication constraints. This technique uses "garbage alignment," i.e., aligning computations in coded computing that are not a part of the desired output. Generalized PolyDot codes bridge between Polynomial codes and MatDot codes, trading off between recovery threshold and communication costs. Second, we demonstrate that Generalized PolyDot can be used for training large Deep Neural Networks (DNNs) on unreliable nodes prone to soft-errors. This requires us to address three additional challenges: (i) prohibitively large overhead of coding the weight matrices in each layer of the DNN at each iteration; (ii) nonlinear operations during training, which are incompatible with linear coding; and (iii) not assuming presence of an error-free master node, requiring us to architect a fully decentralized implementation without any "single point of failure." We allow all primary DNN training steps, namely, matrix multiplication, nonlinear activation, Hadamard product, and update steps as well as the encoding/decoding to be error-prone. We consider the case of mini-batch size $B=1$, as well as $B>1$, leveraging coded matrix-vector products, and matrix-matrix products respectively. The problem of DNN training under soft-errors also motivates an interesting, probabilistic error model under which a real number $(P,Q)$ MDS code is shown to correct $P-Q-1$ errors with probability $1$ as compared to $\lfloor \frac{P-Q}{2} \rfloor$ for the more conventional, adversarial error model. We also demonstrate that our proposed strategy can provide unbounded gains in error tolerance over a competing replication strategy and a preliminary MDS-code-based strategy for both these error models.

High Performance Zero-Memory Overhead Direct Convolutions

The computation of convolution layers in deep neural networks typically rely on high performance routines that trade space for time by using additional memory (either for packing purposes or required as part of the algorithm) to improve performance. The problems with such an approach are two-fold. First, these routines incur additional memory overhead which reduces the overall size of the network that can fit on embedded devices with limited memory capacity. Second, these high performance routines were not optimized for performing convolution, which means that the performance obtained is usually less than conventionally expected. In this paper, we demonstrate that direct convolution, when implemented correctly, eliminates all memory overhead, and yields performance that is between 10% to 400% times better than existing high performance implementations of convolution layers on conventional and embedded CPU architectures. We also show that a high performance direct convolution exhibits better scaling performance, i.e. suffers less performance drop, when increasing the number of threads.