Testing Changes in Communities for the Stochastic Block Model

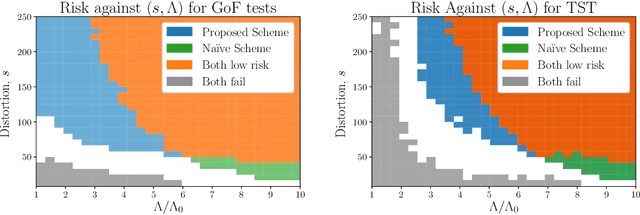
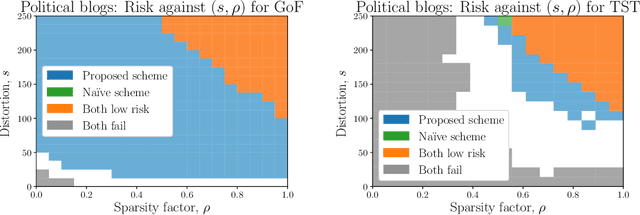
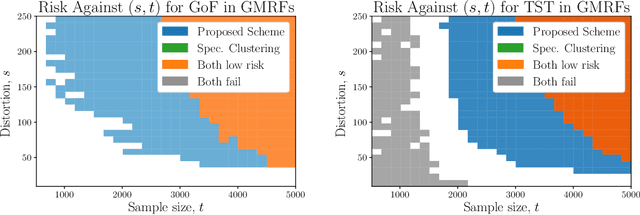
We introduce the problems of goodness-of-fit and two-sample testing of the latent community structure in a 2-community, symmetric, stochastic block model (SBM), in the regime where recovery of the structure is difficult. The latter problem may be described as follows: let $x,y$ be two latent community partitions. Given graphs $G,H$ drawn according to SBMs with partitions $x,y$, respectively, we wish to test the hypothesis $x = y$ against $d(x,y) \ge s,$ for a given Hamming distortion parameter $s \ll n$. Prior work showed that `partial' recovery of these partitions up to distortion $s$ with vanishing error probability requires that the signal-to-noise ratio $(\mathrm{SNR})$ is $\gtrsim C \log (n/s).$ We prove by constructing simple schemes that if $s \gg \sqrt{n \log n},$ then these testing problems can be solved even if $\mathrm{SNR} = O(1).$ For $s = o(\sqrt{n}),$ and constant order degrees, we show via an information-theoretic lower bound that both testing problems require $\mathrm{SNR} = \Omega(\log(n)),$ and thus at this scale the na\"{i}ve scheme of learning the communities and comparing them is minimax optimal up to constant factors. These results are augmented by simulations of goodness-of-fit and two-sample testing for standard SBMs as well as for Gaussian Markov random fields with underlying SBM structure.