Scalarizing Multi-Objective Robot Planning Problems using Weighted Maximization

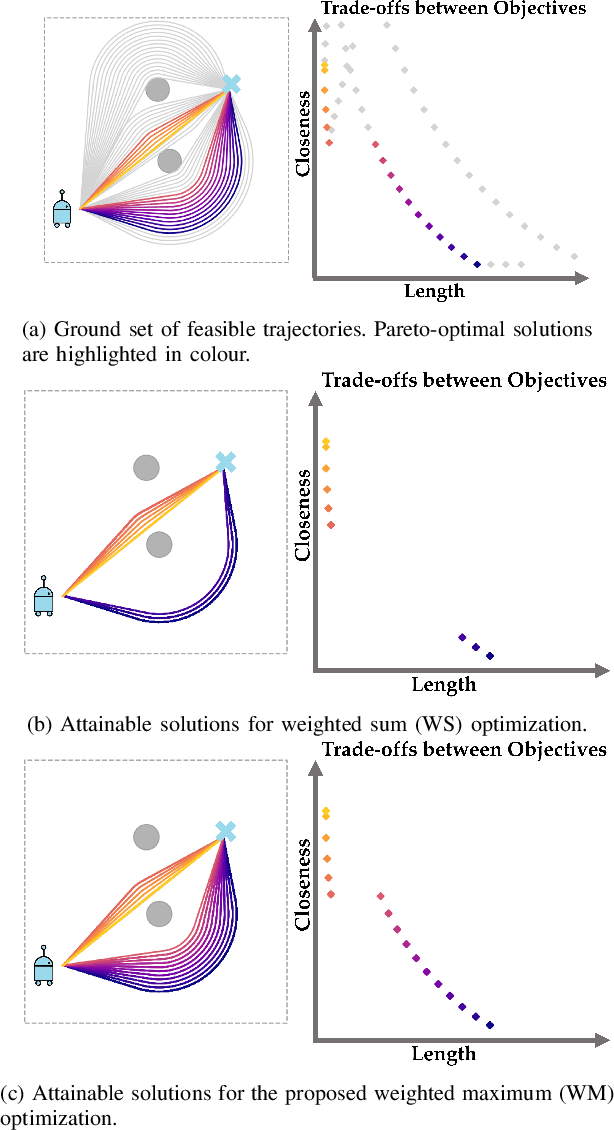
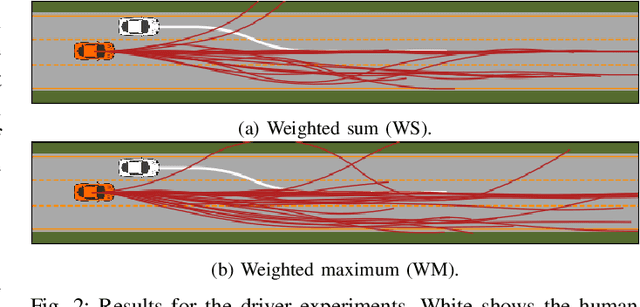
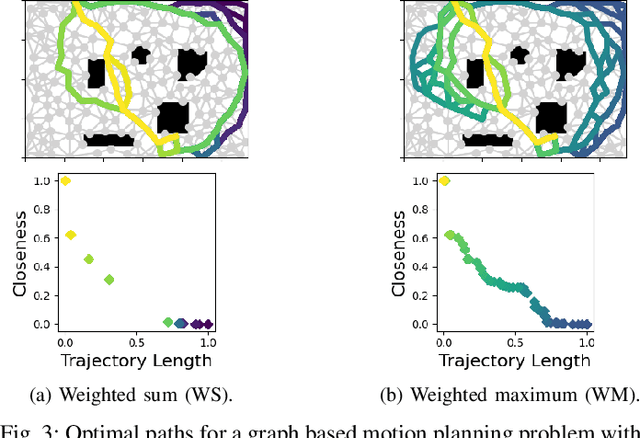
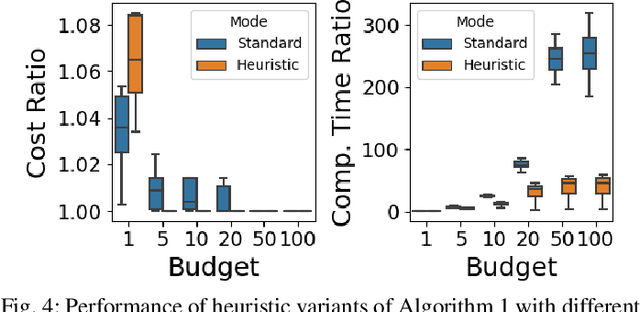
When designing a motion planner for autonomous robots there are usually multiple objectives to be considered. However, a cost function that yields the desired trade-off between objectives is not easily obtainable. A common technique across many applications is to use a weighted sum of relevant objective functions and then carefully adapt the weights. However, this approach may not find all relevant trade-offs even in simple planning problems. Thus, we study an alternative method based on a weighted maximum of objectives. Such a cost function is more expressive than the weighted sum, and we show how it can be deployed in both continuous- and discrete-space motion planning problems. We propose a novel path planning algorithm for the proposed cost function and establish its correctness, and present heuristic adaptations that yield a practical runtime. In extensive simulation experiments, we demonstrate that the proposed cost function and algorithm are able to find a wider range of trade-offs between objectives (i.e., Pareto-optimal solutions) for various planning problems, showcasing its advantages in practice.

Statistically Distinct Plans for Multi-Objective Task Assignment

We study the problem of finding statistically distinct plans for stochastic planning and task assignment problems such as online multi-robot pickup and delivery (MRPD) when facing multiple competing objectives. In many real-world settings robot fleets do not only need to fulfil delivery requests, but also have to consider auxiliary objectives such as energy efficiency or avoiding human-centered work spaces. We pose MRPD as a multi-objective optimization problem where the goal is to find MRPD policies that yield different trade-offs between given objectives. There are two main challenges: 1) MRPD is computationally hard, which limits the number of trade-offs that can reasonably be computed, and 2) due to the random task arrivals, one needs to consider statistical variance of the objective values in addition to the average. We present an adaptive sampling algorithm that finds a set of policies which i) are approximately optimal, ii) approximate the set of all optimal solutions, and iii) are statistically distinguishable. We prove completeness and adapt a state-of-the-art MRPD solver to the multi-objective setting for three example objectives. In a series of simulation experiments we demonstrate the advantages of the proposed method compared to baseline approaches and show its robustness in a sensitivity analysis. The approach is general and could be adapted to other multi-objective task assignment and planning problems under uncertainty.

Designing Heterogeneous Robot Fleets for Task Allocation and Sequencing

We study the problem of selecting a fleet of robots to service spatially distributed tasks with diverse requirements within time-windows. The problem of allocating tasks to a fleet of potentially heterogeneous robots and finding an optimal sequence for each robot is known as multi-robot task assignment (MRTA). Most state-of-the-art methods focus on the problem when the fleet of robots is fixed. In contrast, we consider that we are given a set of available robot types and requested tasks, and need to assemble a fleet that optimally services the tasks while the cost of the fleet remains under a budget limit. We characterize the complexity of the problem and provide a Mixed-Integer Linear Program (MILP) formulation. Due to poor scalability of the MILP, we propose a heuristic solution based on a Large Neighbourhood Search (LNS). In simulations, we demonstrate that the proposed method requires substantially lower budgets than a greedy algorithm to service all tasks.

Optimizing Task Waiting Times in Dynamic Vehicle Routing

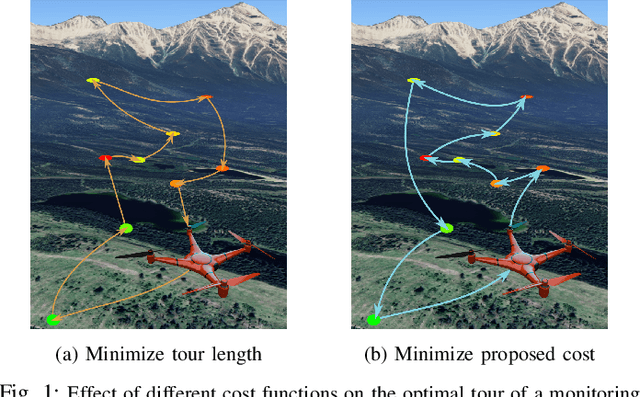
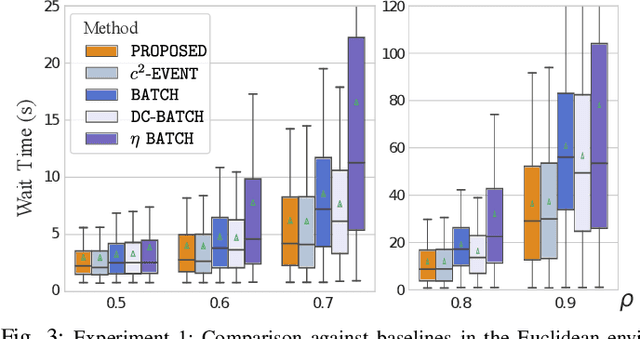
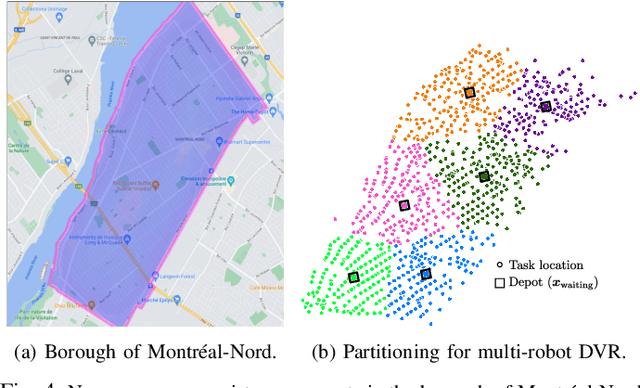
We study the problem of deploying a fleet of mobile robots to service tasks that arrive stochastically over time and at random locations in an environment. This is known as the Dynamic Vehicle Routing Problem (DVRP) and requires robots to allocate incoming tasks among themselves and find an optimal sequence for each robot. State-of-the-art approaches only consider average wait times and focus on high-load scenarios where the arrival rate of tasks approaches the limit of what can be handled by the robots while keeping the queue of unserviced tasks bounded, i.e., stable. To ensure stability, these approaches repeatedly compute minimum distance tours over a set of newly arrived tasks. This paper is aimed at addressing the missing policies for moderate-load scenarios, where quality of service can be improved by prioritizing long-waiting tasks. We introduce a novel DVRP policy based on a cost function that takes the $p$-norm over accumulated wait times and show it guarantees stability even in high-load scenarios. We demonstrate that the proposed policy outperforms the state-of-the-art in both mean and $95^{th}$ percentile wait times in moderate-load scenarios through simulation experiments in the Euclidean plane as well as using real-world data for city scale service requests.

Approximation Algorithms for Robot Tours in Random Fields with Guaranteed Estimation Accuracy

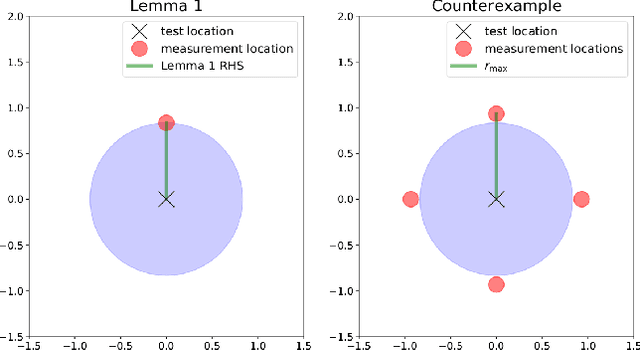
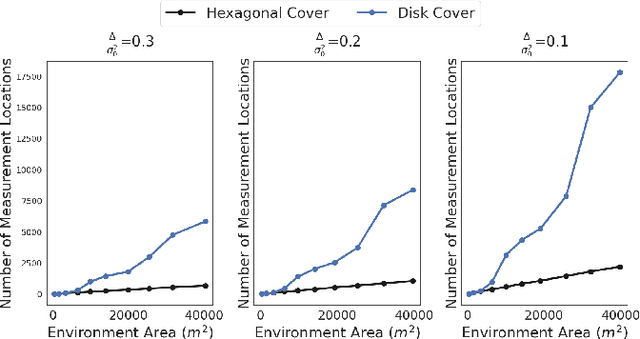
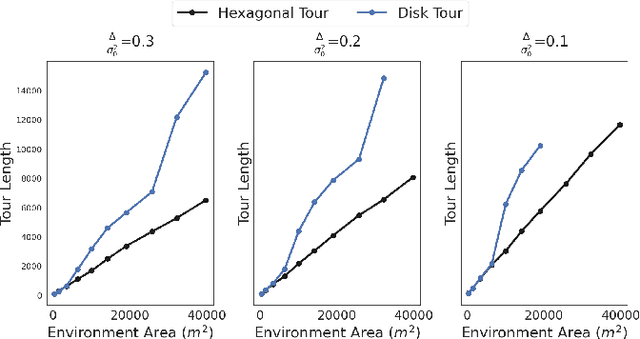
We study the sample placement and shortest tour problem for robots tasked with mapping environmental phenomena modeled as stationary random fields. The objective is to minimize the resources used (samples or tour length) while guaranteeing estimation accuracy. We give approximation algorithms for both problems in convex environments. These improve previously known results, both in terms of theoretical guarantees and in simulations. In addition, we disprove an existing claim in the literature on a lower bound for a solution to the sample placement problem.

Scheduling Operator Assistance for Shared Autonomy in Multi-Robot Teams

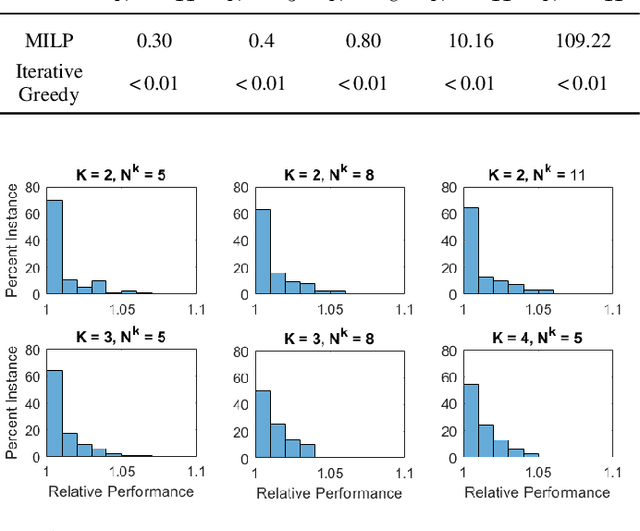
In this paper, we consider the problem of allocating human operator assistance in a system with multiple autonomous robots. Each robot is required to complete independent missions, each defined as a sequence of tasks. While executing a task, a robot can either operate autonomously or be teleoperated by the human operator to complete the task at a faster rate. We show that the problem of creating a teleoperation schedule that minimizes makespan of the system is NP-Hard. We formulate our problem as a Mixed Integer Linear Program, which can be used to optimally solve small to moderate sized problem instances. We also develop an anytime algorithm that makes use of the problem structure to provide a fast and high-quality solution of the operator scheduling problem, even for larger problem instances. Our key insight is to identify blocking tasks in greedily-created schedules and iteratively remove those blocks to improve the quality of the solution. Through numerical simulations, we demonstrate the benefits of the proposed algorithm as an efficient and scalable approach that outperforms other greedy methods.

Error-Bounded Approximation of Pareto Fronts in Robot Planning Problems

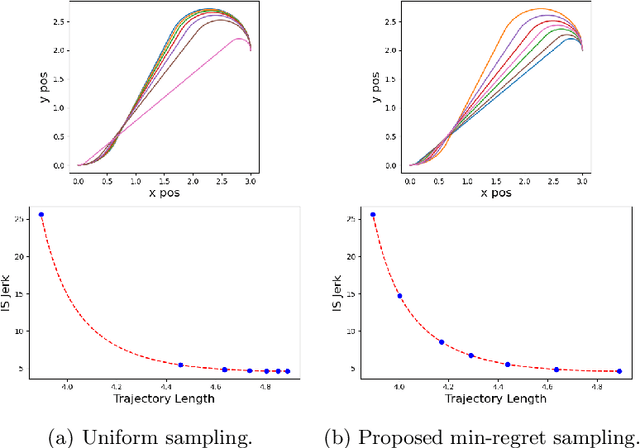
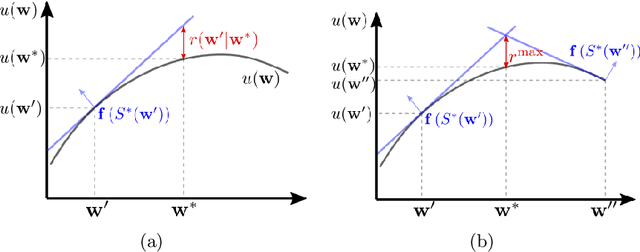
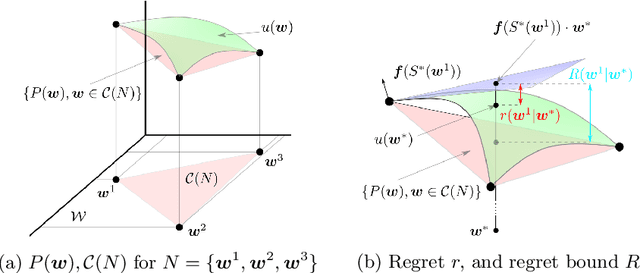
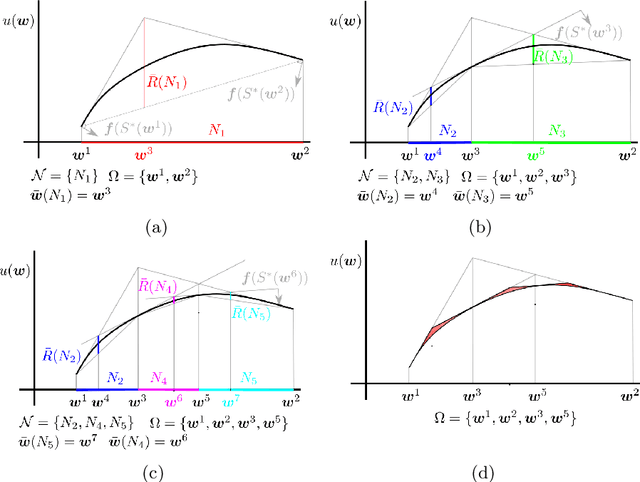
Many problems in robotics seek to simultaneously optimize several competing objectives under constraints. A conventional approach to solving such multi-objective optimization problems is to create a single cost function comprised of the weighted sum of the individual objectives. Solutions to this scalarized optimization problem are Pareto optimal solutions to the original multi-objective problem. However, finding an accurate representation of a Pareto front remains an important challenge. Using uniformly spaced weight vectors is often inefficient and does not provide error bounds. Thus, we address the problem of computing a finite set of weight vectors such that for any other weight vector, there exists an element in the set whose error compared to optimal is minimized. To this end, we prove fundamental properties of the optimal cost as a function of the weight vector, including its continuity and concavity. Using these, we propose an algorithm that greedily adds the weight vector least-represented by the current set, and provide bounds on the error. Finally, we illustrate that the proposed approach significantly outperforms uniformly distributed weights for different robot planning problems with varying numbers of objective functions.

An Improved Greedy Algorithm for Subset Selection in Linear Estimation

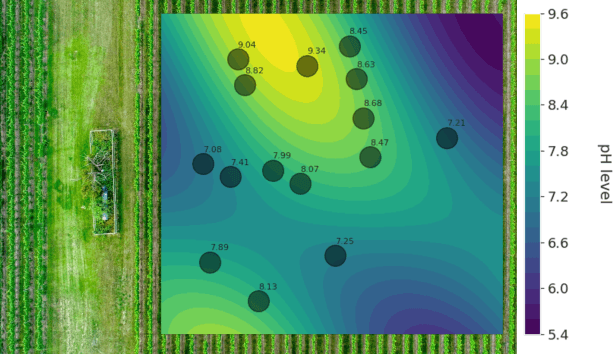
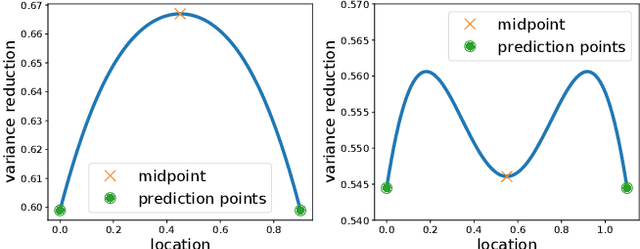
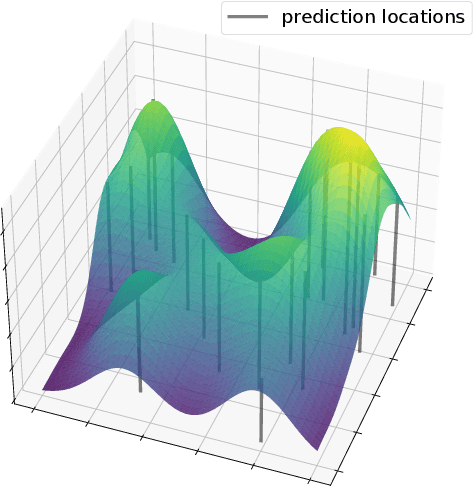
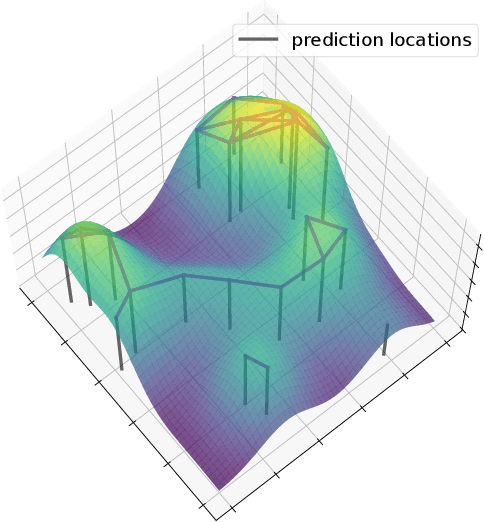
In this paper, we consider a subset selection problem in a spatial field where we seek to find a set of k locations whose observations provide the best estimate of the field value at a finite set of prediction locations. The measurements can be taken at any location in the continuous field, and the covariance between the field values at different points is given by the widely used squared exponential covariance function. One approach for observation selection is to perform a grid discretization of the space and obtain an approximate solution using the greedy algorithm. The solution quality improves with a finer grid resolution but at the cost of increased computation. We propose a method to reduce the computational complexity, or conversely to increase solution quality, of the greedy algorithm by considering a search space consisting only of prediction locations and centroids of cliques formed by the prediction locations. We demonstrate the effectiveness of our proposed approach in simulation, both in terms of solution quality and runtime.

Learning Submodular Objectives for Team Environmental Monitoring

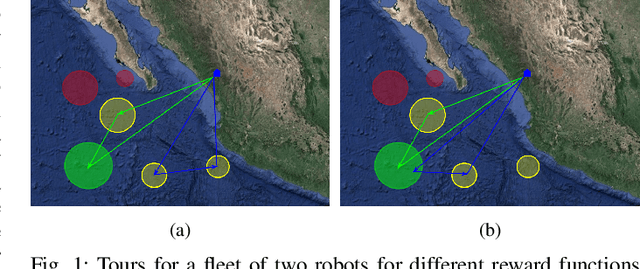
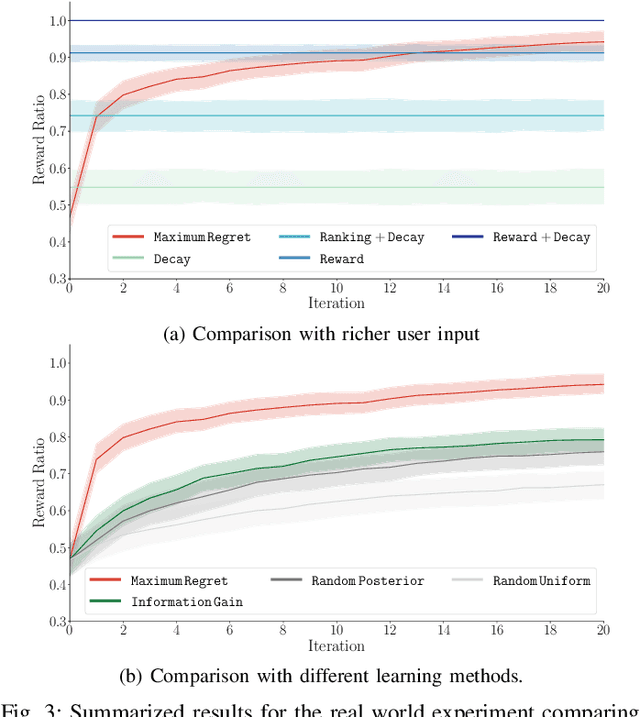
In this paper, we study the well-known team orienteering problem where a fleet of robots collects rewards by visiting locations. Usually, the rewards are assumed to be known to the robots; however, in applications such as environmental monitoring or scene reconstruction, the rewards are often subjective and specifying them is challenging. We propose a framework to learn the unknown preferences of the user by presenting alternative solutions to them, and the user provides a ranking on the proposed alternative solutions. We consider the two cases for the user: 1) a deterministic user which provides the optimal ranking for the alternative solutions, and 2) a noisy user which provides the optimal ranking according to an unknown probability distribution. For the deterministic user we propose a framework to minimize a bound on the maximum deviation from the optimal solution, namely regret. We adapt the approach to capture the noisy user and minimize the expected regret. Finally, we demonstrate the importance of learning user preferences and the performance of the proposed methods in an extensive set of experimental results using real world datasets for environmental monitoring problems.

Learning Reward Functions from Scale Feedback

Today's robots are increasingly interacting with people and need to efficiently learn inexperienced user's preferences. A common framework is to iteratively query the user about which of two presented robot trajectories they prefer. While this minimizes the users effort, a strict choice does not yield any information on how much one trajectory is preferred. We propose scale feedback, where the user utilizes a slider to give more nuanced information. We introduce a probabilistic model on how users would provide feedback and derive a learning framework for the robot. We demonstrate the performance benefit of slider feedback in simulations, and validate our approach in two user studies suggesting that scale feedback enables more effective learning in practice.