Error-Bounded Approximation of Pareto Fronts in Robot Planning Problems
Paper and Code
Jun 01, 2022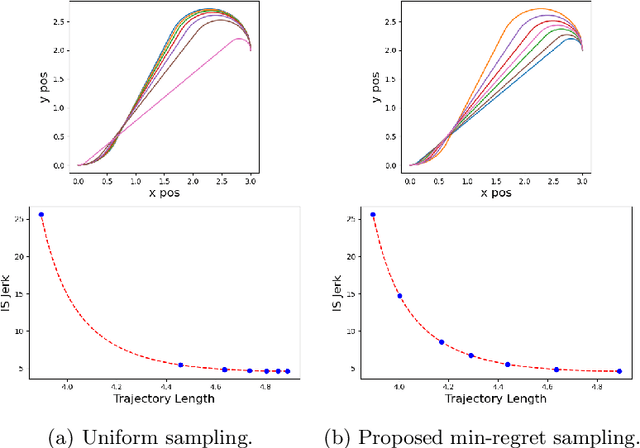
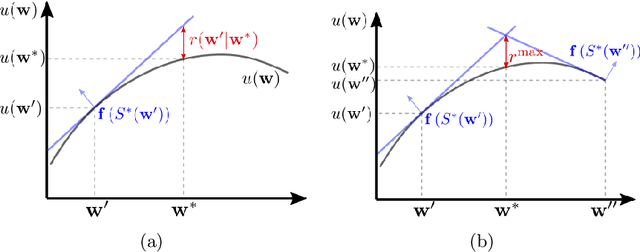
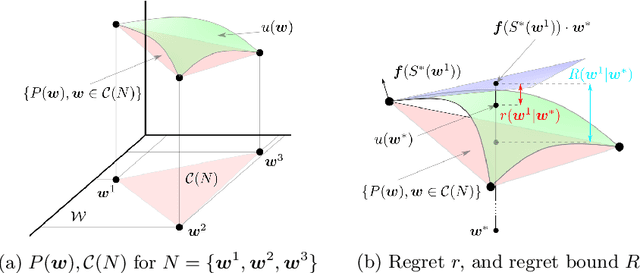
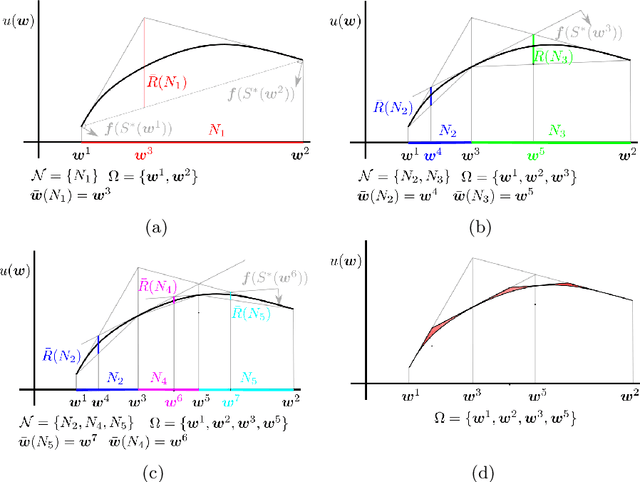
Many problems in robotics seek to simultaneously optimize several competing objectives under constraints. A conventional approach to solving such multi-objective optimization problems is to create a single cost function comprised of the weighted sum of the individual objectives. Solutions to this scalarized optimization problem are Pareto optimal solutions to the original multi-objective problem. However, finding an accurate representation of a Pareto front remains an important challenge. Using uniformly spaced weight vectors is often inefficient and does not provide error bounds. Thus, we address the problem of computing a finite set of weight vectors such that for any other weight vector, there exists an element in the set whose error compared to optimal is minimized. To this end, we prove fundamental properties of the optimal cost as a function of the weight vector, including its continuity and concavity. Using these, we propose an algorithm that greedily adds the weight vector least-represented by the current set, and provide bounds on the error. Finally, we illustrate that the proposed approach significantly outperforms uniformly distributed weights for different robot planning problems with varying numbers of objective functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge