AUTO-IceNav: A Local Navigation Strategy for Autonomous Surface Ships in Broken Ice Fields

Ice conditions often require ships to reduce speed and deviate from their main course to avoid damage to the ship. In addition, broken ice fields are becoming the dominant ice conditions encountered in the Arctic, where the effects of collisions with ice are highly dependent on where contact occurs and on the particular features of the ice floes. In this paper, we present AUTO-IceNav, a framework for the autonomous navigation of ships operating in ice floe fields. Trajectories are computed in a receding-horizon manner, where we frequently replan given updated ice field data. During a planning step, we assume a nominal speed that is safe with respect to the current ice conditions, and compute a reference path. We formulate a novel cost function that minimizes the kinetic energy loss of the ship from ship-ice collisions and incorporate this cost as part of our lattice-based path planner. The solution computed by the lattice planning stage is then used as an initial guess in our proposed optimization-based improvement step, producing a locally optimal path. Extensive experiments were conducted both in simulation and in a physical testbed to validate our approach.

Optimizing Task Waiting Times in Dynamic Vehicle Routing

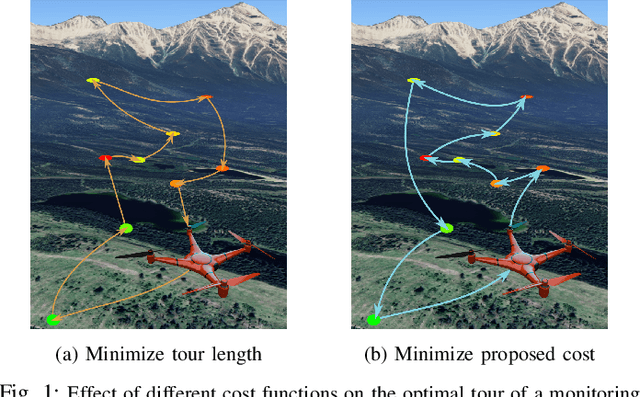
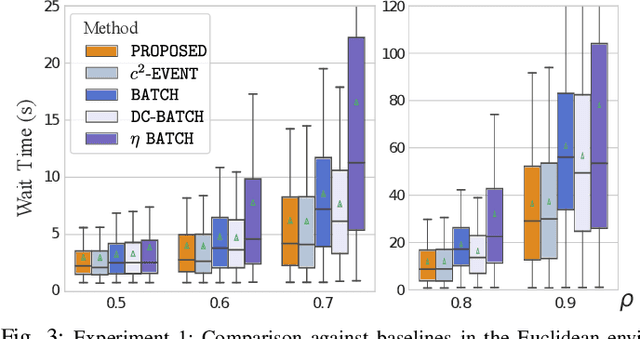
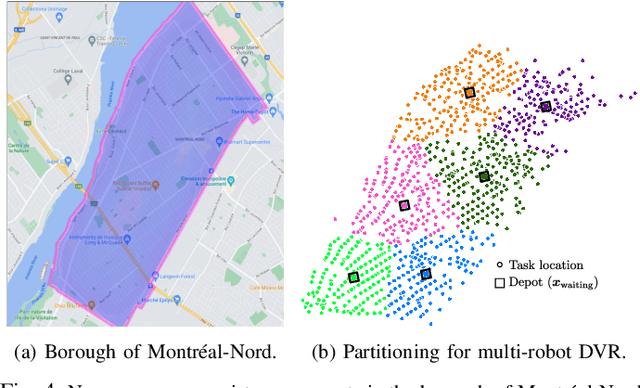
We study the problem of deploying a fleet of mobile robots to service tasks that arrive stochastically over time and at random locations in an environment. This is known as the Dynamic Vehicle Routing Problem (DVRP) and requires robots to allocate incoming tasks among themselves and find an optimal sequence for each robot. State-of-the-art approaches only consider average wait times and focus on high-load scenarios where the arrival rate of tasks approaches the limit of what can be handled by the robots while keeping the queue of unserviced tasks bounded, i.e., stable. To ensure stability, these approaches repeatedly compute minimum distance tours over a set of newly arrived tasks. This paper is aimed at addressing the missing policies for moderate-load scenarios, where quality of service can be improved by prioritizing long-waiting tasks. We introduce a novel DVRP policy based on a cost function that takes the $p$-norm over accumulated wait times and show it guarantees stability even in high-load scenarios. We demonstrate that the proposed policy outperforms the state-of-the-art in both mean and $95^{th}$ percentile wait times in moderate-load scenarios through simulation experiments in the Euclidean plane as well as using real-world data for city scale service requests.

Real-Time Navigation for Autonomous Surface Vehicles In Ice-Covered Waters

Vessel transit in ice-covered waters poses unique challenges in safe and efficient motion planning. When the concentration of ice is high, it may not be possible to find collision-free trajectories. Instead, ice can be pushed out of the way if it is small or if contact occurs near the edge of the ice. In this work, we propose a real-time navigation framework that minimizes collisions with ice and distance travelled by the vessel. We exploit a lattice-based planner with a cost that captures the ship interaction with ice. To address the dynamic nature of the environment, we plan motion in a receding horizon manner based on updated vessel and ice state information. Further, we present a novel planning heuristic for evaluating the cost-to-go, which is applicable to navigation in a channel without a fixed goal location. The performance of our planner is evaluated across several levels of ice concentration both in simulated and in real-world experiments.

Error-Bounded Approximation of Pareto Fronts in Robot Planning Problems

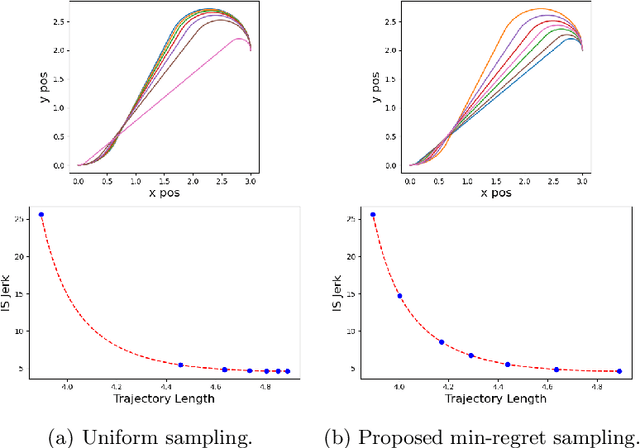
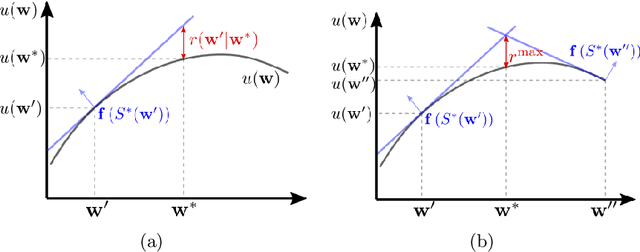
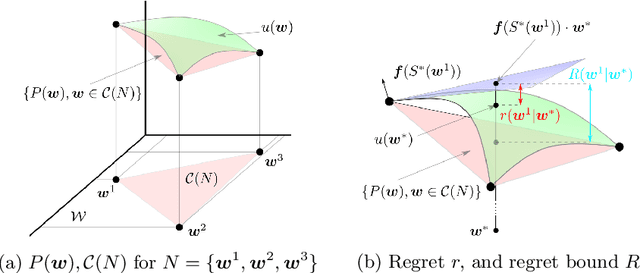
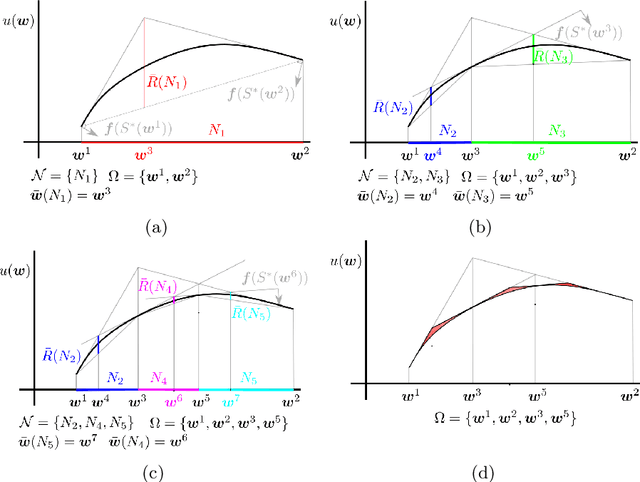
Many problems in robotics seek to simultaneously optimize several competing objectives under constraints. A conventional approach to solving such multi-objective optimization problems is to create a single cost function comprised of the weighted sum of the individual objectives. Solutions to this scalarized optimization problem are Pareto optimal solutions to the original multi-objective problem. However, finding an accurate representation of a Pareto front remains an important challenge. Using uniformly spaced weight vectors is often inefficient and does not provide error bounds. Thus, we address the problem of computing a finite set of weight vectors such that for any other weight vector, there exists an element in the set whose error compared to optimal is minimized. To this end, we prove fundamental properties of the optimal cost as a function of the weight vector, including its continuity and concavity. Using these, we propose an algorithm that greedily adds the weight vector least-represented by the current set, and provide bounds on the error. Finally, we illustrate that the proposed approach significantly outperforms uniformly distributed weights for different robot planning problems with varying numbers of objective functions.

Multi-Start n-Dimensional Lattice Planning with Optimal Motion Primitives

In the field of motion planning the use of pre-computed, feasible, locally optimal motions called motion primitives can not only increase the quality of motions, but decrease the computation time required to develop these motions. In this work we extend the results of our earlier work by developing a technique for computing primitives for a lattice that admits higher-order states like curvature, velocity, and acceleration. The technique involves computing a minimal set of motion primitives that $t$-span a configuration space lattice. A set of motion primitives $t$-span a lattice if, given a real number $t$ greater or equal to one, any configuration in the lattice can be reached via a sequence of motion primitives whose cost is no more than $t$ times the cost of the optimal path to that configuration. While motion primitives computed in this way could be used with any graph search algorithm to develop a motion, this paper also proposes one such algorithm which works well in practice in both short complex maneuvers and longer maneuvers. Finally, this paper proposes a shortcut-based smoothing algorithm based on shortest path planning in directed acyclic graphs.

Tunable Trajectory Planner Using G3 Curves

Trajectory planning is commonly used as part of a local planner in autonomous driving. This paper considers the problem of planning a continuous-curvature-rate trajectory between fixed start and goal states that minimizes a tunable trade-off between passenger comfort and travel time. The problem is an instance of infinite dimensional optimization over two continuous functions: a path, and a velocity profile. We propose a simplification of this problem that facilitates the discretization of both functions. This paper also proposes a method to quickly generate minimal-length paths between start and goal states based on a single tuning parameter: the second derivative of curvature. Furthermore, we discretize the set of velocity profiles along a given path into a selection of acceleration way-points along the path. Gradient-descent is then employed to minimize cost over feasible choices of the second derivative of curvature, and acceleration way-points, resulting in a method that repeatedly solves the path and velocity profiles in an iterative fashion. Numerical examples are provided to illustrate the benefits of the proposed methods.

Computing a Minimal Set of t-Spanning Motion Primitives for Lattice Planners

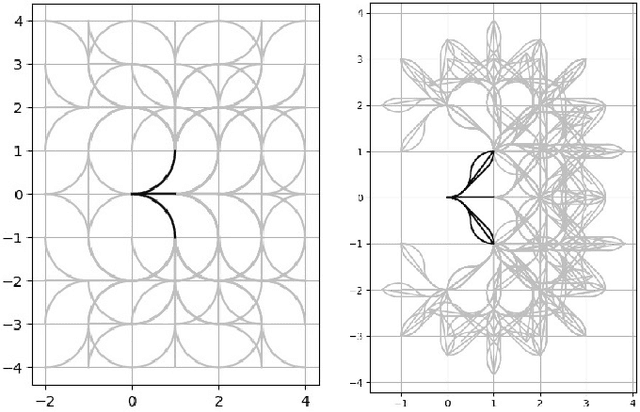
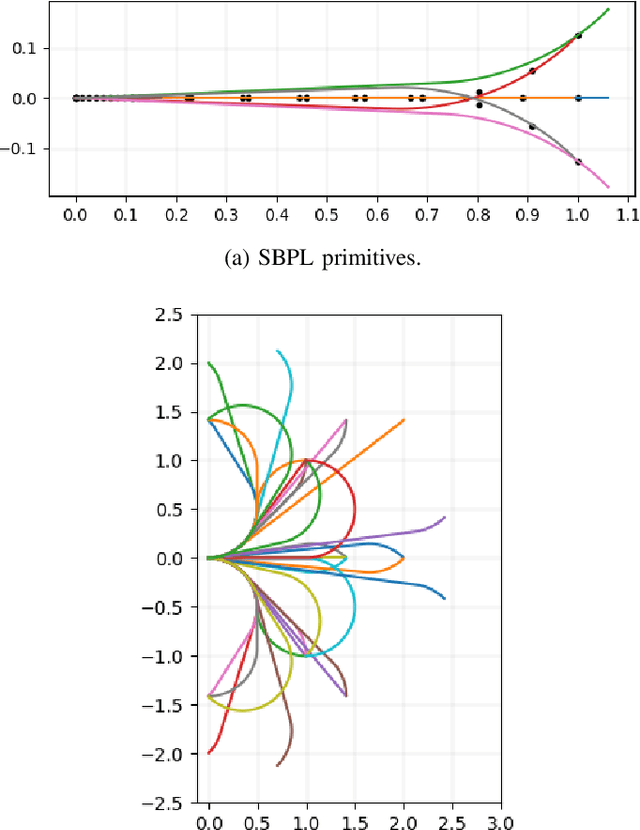
In this paper we consider the problem of computing an optimal set of motion primitives for a lattice planner. The objective we consider is to compute a minimal set of motion primitives that t-span a configuration space lattice. A set of motion primitives t-span a lattice if, given a real number t greater or equal to one, any configuration in the lattice can be reached via a sequence of motion primitives whose cost is no more than t times the cost of the optimal path to that configuration. Determining the smallest set of t-spanning motion primitives allows for quick traversal of a state lattice in the context of robotic motion planning, while maintaining a t-factor adherence to the theoretically optimal path. While several heuristics exist to determine a t-spanning set of motion primitives, these are presented without guarantees on the size of the set relative to optimal. This paper provides a proof that the minimal t-spanning control set problem for a lattice defined over an arbitrary robot configuration space is NP-complete, and presents a compact mixed integer linear programming formulation to compute an optimal t-spanner. We show that solutions obtained by the mixed integer linear program have significantly fewer motion primitives than state of the art heuristic algorithms, and out perform a set of standard primitives used in robotic path planning.