Estimating Visibility from Alternate Perspectives for Motion Planning with Occlusions

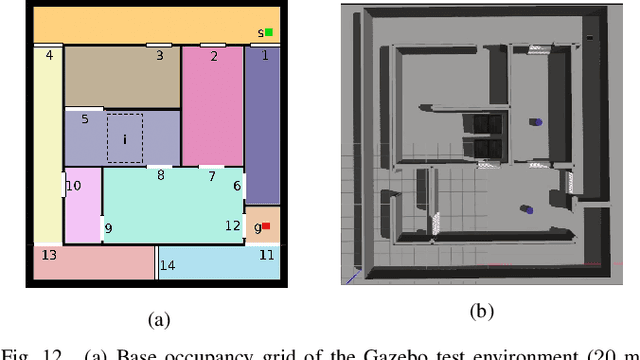
Visibility is a crucial aspect of planning and control of autonomous vehicles (AV), particularly when navigating environments with occlusions. However, when an AV follows a trajectory with multiple occlusions, existing methods evaluate each occlusion individually, calculate a visibility cost for each, and rely on the planner to minimize the overall cost. This can result in conflicting priorities for the planner, as individual occlusion costs may appear to be in opposition. We solve this problem by creating an alternate perspective cost map that allows for an aggregate view of the occlusions in the environment. The value of each cell on the cost map is a measure of the amount of visual information that the vehicle can gain about the environment by visiting that location. Our proposed method identifies observation locations and occlusion targets drawn from both map data and sensor data. We show how to estimate an alternate perspective for each observation location and then combine all estimates into a single alternate perspective cost map for motion planning.

Optimizing Task Waiting Times in Dynamic Vehicle Routing

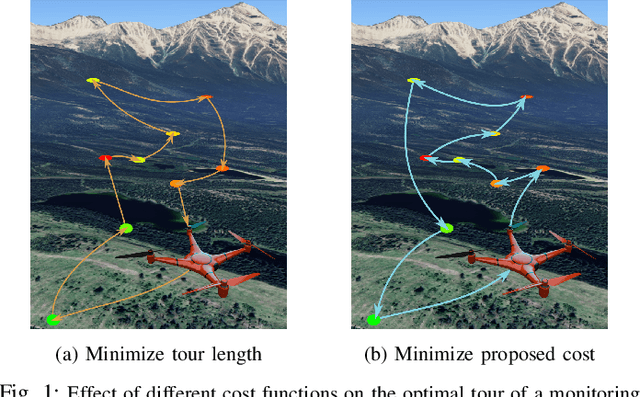
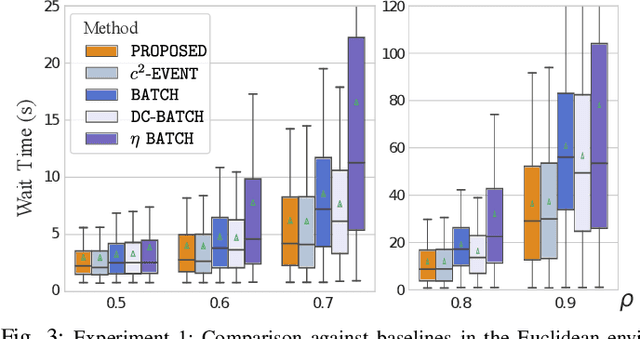
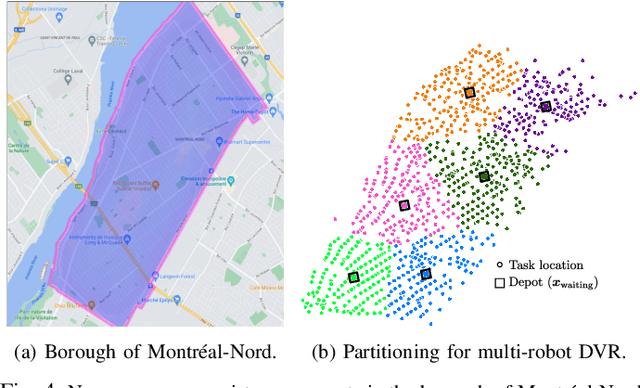
We study the problem of deploying a fleet of mobile robots to service tasks that arrive stochastically over time and at random locations in an environment. This is known as the Dynamic Vehicle Routing Problem (DVRP) and requires robots to allocate incoming tasks among themselves and find an optimal sequence for each robot. State-of-the-art approaches only consider average wait times and focus on high-load scenarios where the arrival rate of tasks approaches the limit of what can be handled by the robots while keeping the queue of unserviced tasks bounded, i.e., stable. To ensure stability, these approaches repeatedly compute minimum distance tours over a set of newly arrived tasks. This paper is aimed at addressing the missing policies for moderate-load scenarios, where quality of service can be improved by prioritizing long-waiting tasks. We introduce a novel DVRP policy based on a cost function that takes the $p$-norm over accumulated wait times and show it guarantees stability even in high-load scenarios. We demonstrate that the proposed policy outperforms the state-of-the-art in both mean and $95^{th}$ percentile wait times in moderate-load scenarios through simulation experiments in the Euclidean plane as well as using real-world data for city scale service requests.

Error-Bounded Approximation of Pareto Fronts in Robot Planning Problems

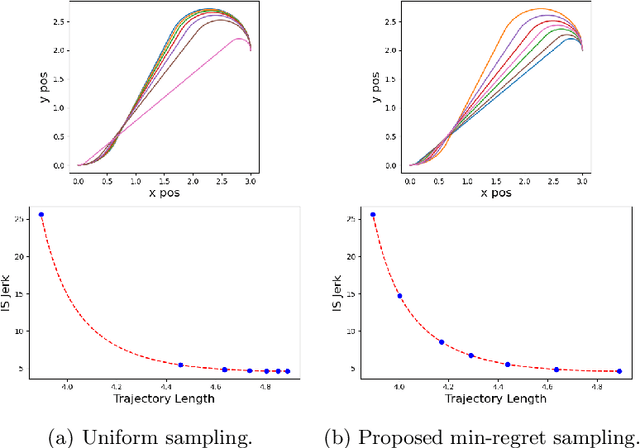
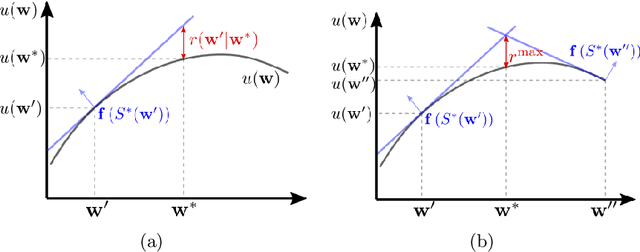
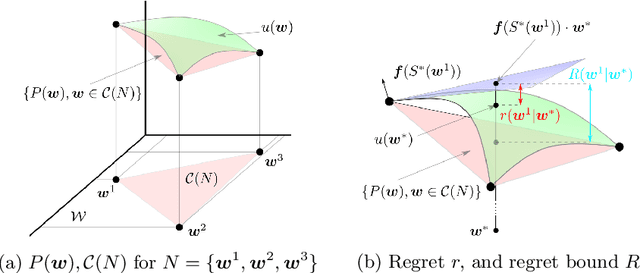
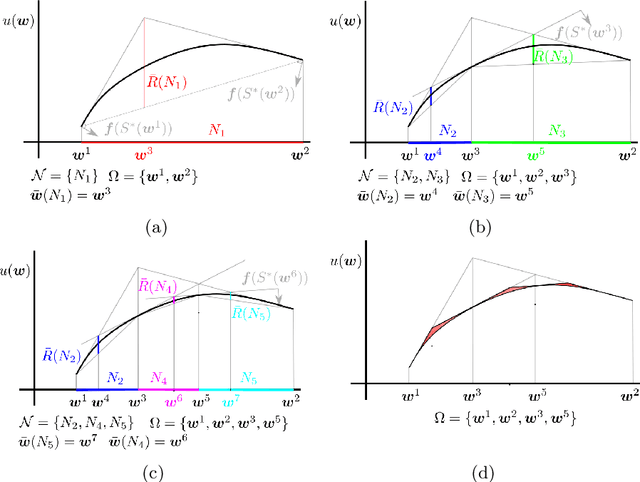
Many problems in robotics seek to simultaneously optimize several competing objectives under constraints. A conventional approach to solving such multi-objective optimization problems is to create a single cost function comprised of the weighted sum of the individual objectives. Solutions to this scalarized optimization problem are Pareto optimal solutions to the original multi-objective problem. However, finding an accurate representation of a Pareto front remains an important challenge. Using uniformly spaced weight vectors is often inefficient and does not provide error bounds. Thus, we address the problem of computing a finite set of weight vectors such that for any other weight vector, there exists an element in the set whose error compared to optimal is minimized. To this end, we prove fundamental properties of the optimal cost as a function of the weight vector, including its continuity and concavity. Using these, we propose an algorithm that greedily adds the weight vector least-represented by the current set, and provide bounds on the error. Finally, we illustrate that the proposed approach significantly outperforms uniformly distributed weights for different robot planning problems with varying numbers of objective functions.

Learning Submodular Objectives for Team Environmental Monitoring

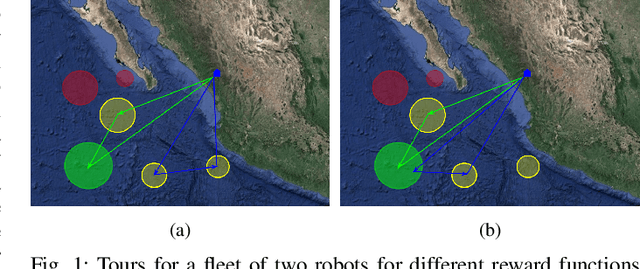
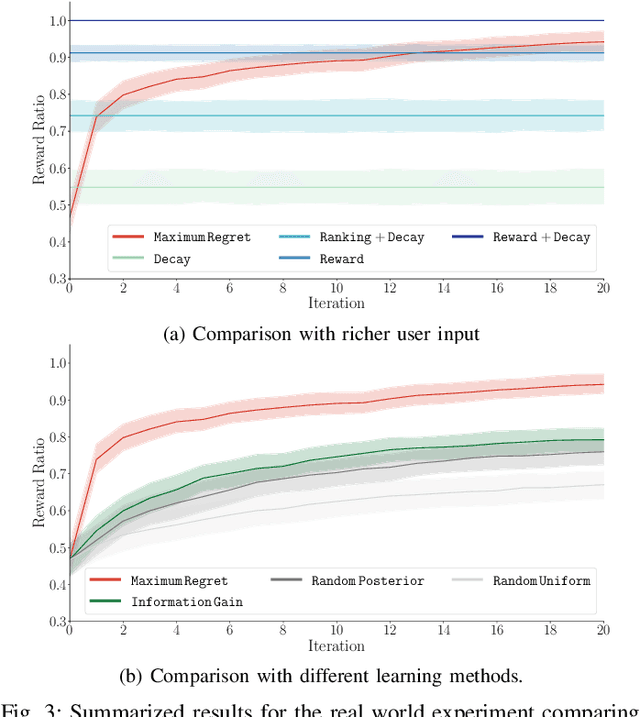
In this paper, we study the well-known team orienteering problem where a fleet of robots collects rewards by visiting locations. Usually, the rewards are assumed to be known to the robots; however, in applications such as environmental monitoring or scene reconstruction, the rewards are often subjective and specifying them is challenging. We propose a framework to learn the unknown preferences of the user by presenting alternative solutions to them, and the user provides a ranking on the proposed alternative solutions. We consider the two cases for the user: 1) a deterministic user which provides the optimal ranking for the alternative solutions, and 2) a noisy user which provides the optimal ranking according to an unknown probability distribution. For the deterministic user we propose a framework to minimize a bound on the maximum deviation from the optimal solution, namely regret. We adapt the approach to capture the noisy user and minimize the expected regret. Finally, we demonstrate the importance of learning user preferences and the performance of the proposed methods in an extensive set of experimental results using real world datasets for environmental monitoring problems.

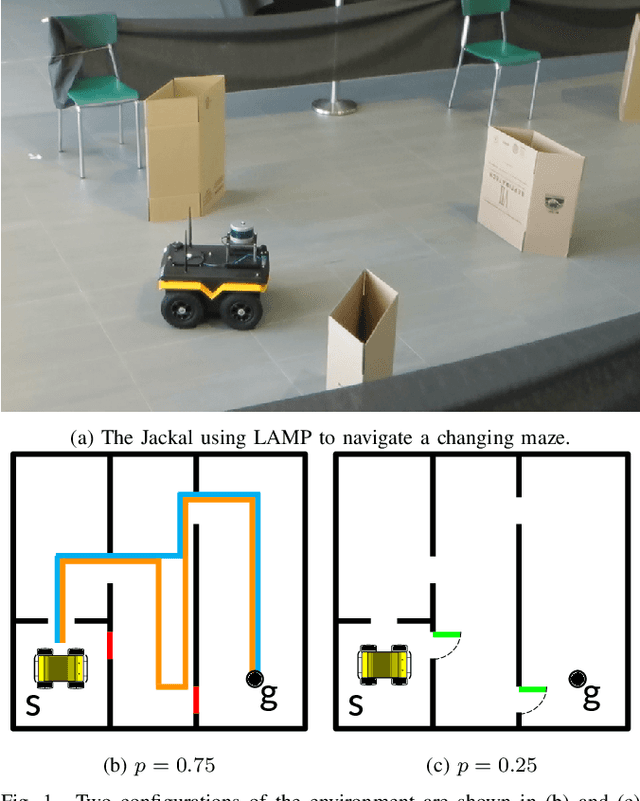
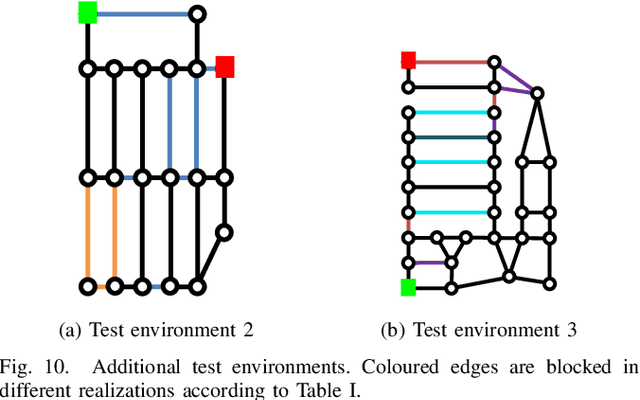
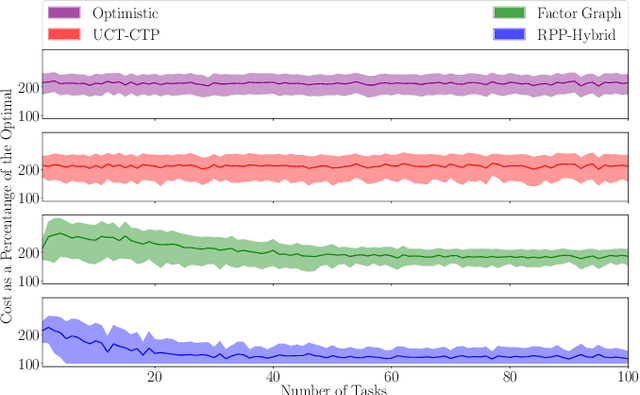
LAMP: Learning a Motion Policy to Repeatedly Navigate in an Uncertain Environment

Mobile robots are often tasked with repeatedly navigating through an environment whose traversability changes over time. These changes may exhibit some hidden structure, which can be learned. Many studies consider reactive algorithms for online planning, however, these algorithms do not take advantage of the past executions of the navigation task for future tasks. In this paper, we formalize the problem of minimizing the total expected cost to perform multiple start-to-goal navigation tasks on a roadmap by introducing the Learned Reactive Planning Problem. We propose a method that captures information from past executions to learn a motion policy to handle obstacles that the robot has seen before. We propose the LAMP framework, which integrates the generated motion policy with an existing navigation stack. Finally, an extensive set of experiments in simulated and real-world environments show that the proposed method outperforms the state-of-the-art algorithms by 10% to 40% in terms of expected time to travel from start to goal. We also evaluate the robustness of the proposed method in the presence of localization and mapping errors on a real robot.

On Efficient Computation of Shortest Dubins Paths Through Three Consecutive Points

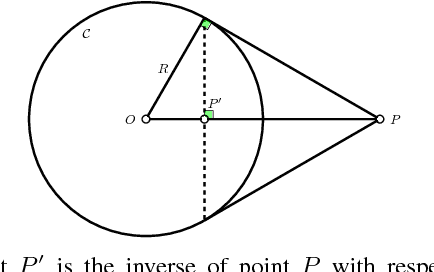
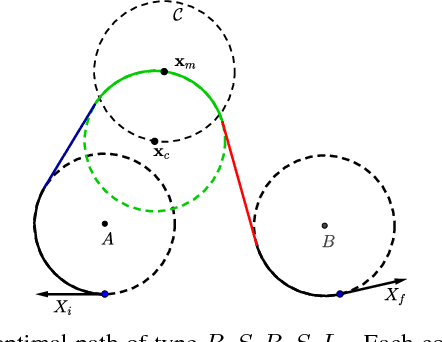
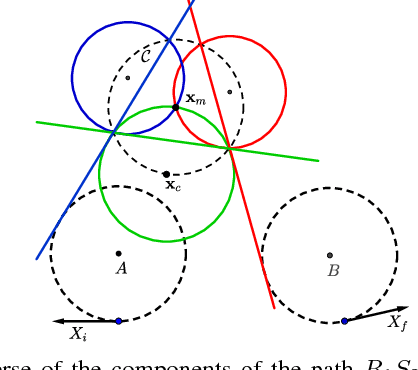
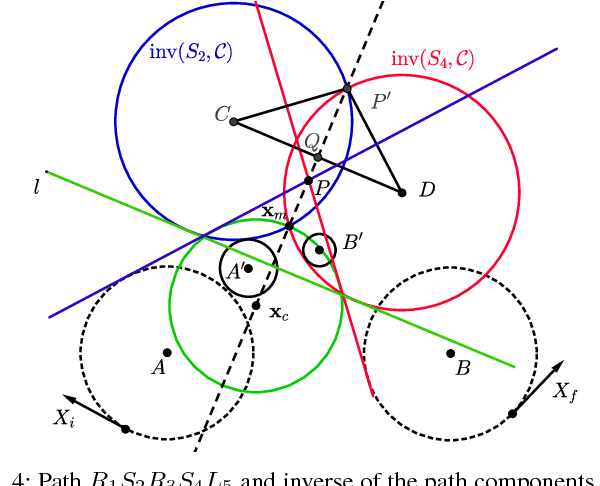
In this paper, we address the problem of computing optimal paths through three consecutive points for the curvature-constrained forward moving Dubins vehicle. Given initial and final configurations of the Dubins vehicle, and a midpoint with an unconstrained heading, the objective is to compute the midpoint heading that minimizes the total Dubins path length. We provide a novel geometrical analysis of the optimal path, and establish new properties of the optimal Dubins' path through three points. We then show how our method can be used to quickly refine Dubins TSP tours produced using state-of-the-art techniques. We also provide extensive simulation results showing the improvement of the proposed approach in both runtime and solution quality over the conventional method of uniform discretization of the heading at the mid-point, followed by solving the minimum Dubins path for each discrete heading.