On Efficient Computation of Shortest Dubins Paths Through Three Consecutive Points
Paper and Code
Sep 21, 2016
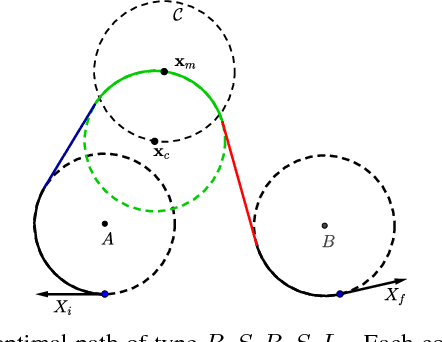
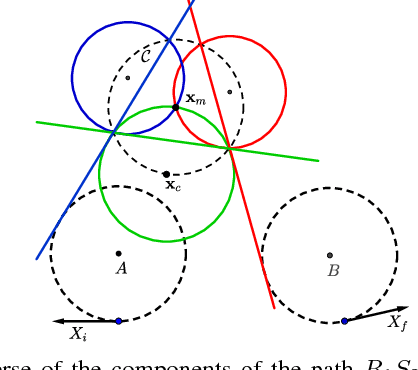
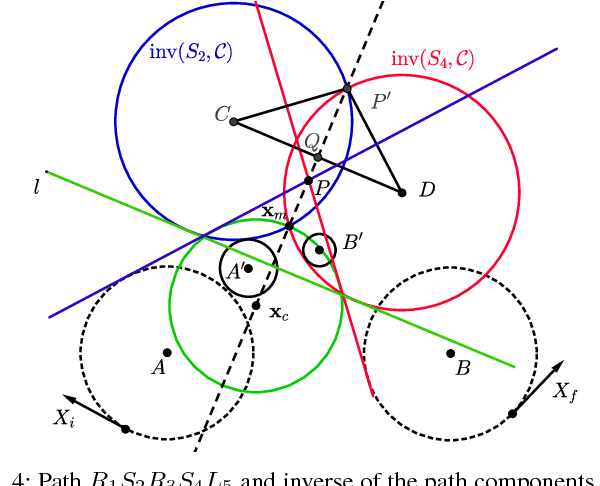
In this paper, we address the problem of computing optimal paths through three consecutive points for the curvature-constrained forward moving Dubins vehicle. Given initial and final configurations of the Dubins vehicle, and a midpoint with an unconstrained heading, the objective is to compute the midpoint heading that minimizes the total Dubins path length. We provide a novel geometrical analysis of the optimal path, and establish new properties of the optimal Dubins' path through three points. We then show how our method can be used to quickly refine Dubins TSP tours produced using state-of-the-art techniques. We also provide extensive simulation results showing the improvement of the proposed approach in both runtime and solution quality over the conventional method of uniform discretization of the heading at the mid-point, followed by solving the minimum Dubins path for each discrete heading.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge