Learning Submodular Objectives for Team Environmental Monitoring
Paper and Code
Dec 15, 2021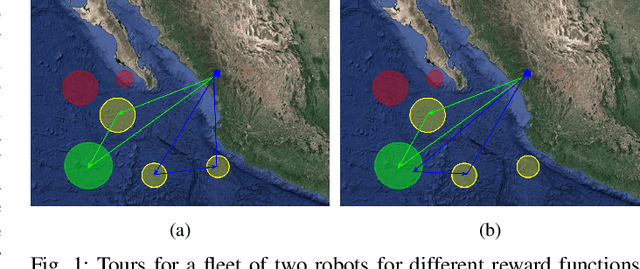

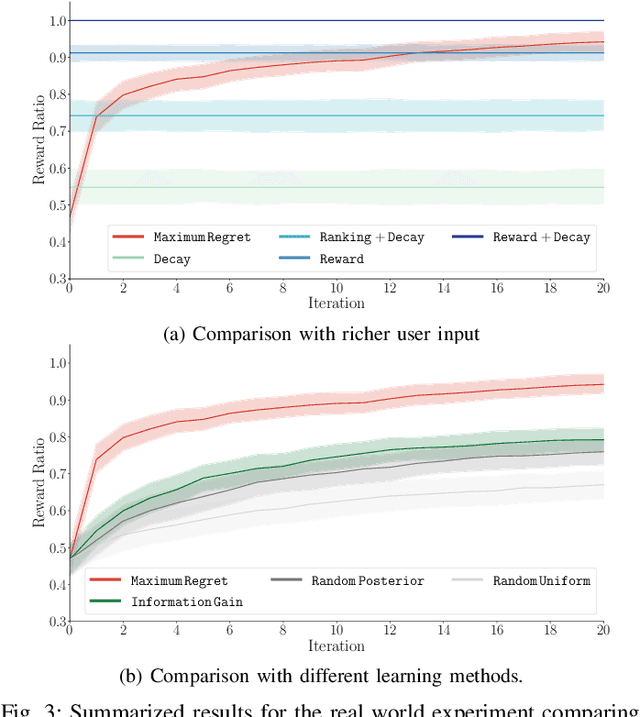
In this paper, we study the well-known team orienteering problem where a fleet of robots collects rewards by visiting locations. Usually, the rewards are assumed to be known to the robots; however, in applications such as environmental monitoring or scene reconstruction, the rewards are often subjective and specifying them is challenging. We propose a framework to learn the unknown preferences of the user by presenting alternative solutions to them, and the user provides a ranking on the proposed alternative solutions. We consider the two cases for the user: 1) a deterministic user which provides the optimal ranking for the alternative solutions, and 2) a noisy user which provides the optimal ranking according to an unknown probability distribution. For the deterministic user we propose a framework to minimize a bound on the maximum deviation from the optimal solution, namely regret. We adapt the approach to capture the noisy user and minimize the expected regret. Finally, we demonstrate the importance of learning user preferences and the performance of the proposed methods in an extensive set of experimental results using real world datasets for environmental monitoring problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge