Nikhil Chopra
Cascade IPG Observer for Underwater Robot State Estimation
Apr 21, 2025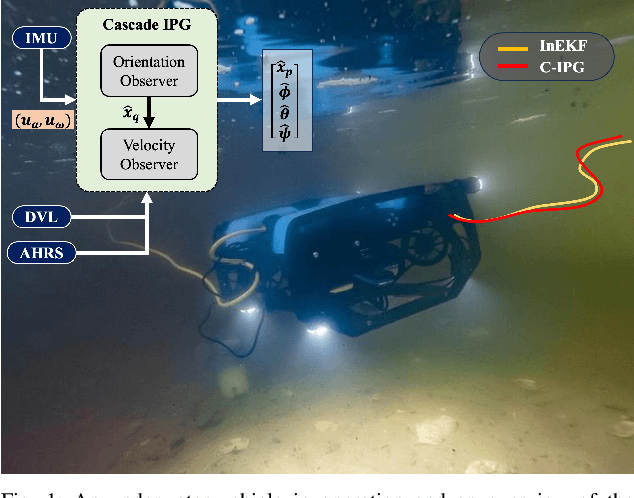
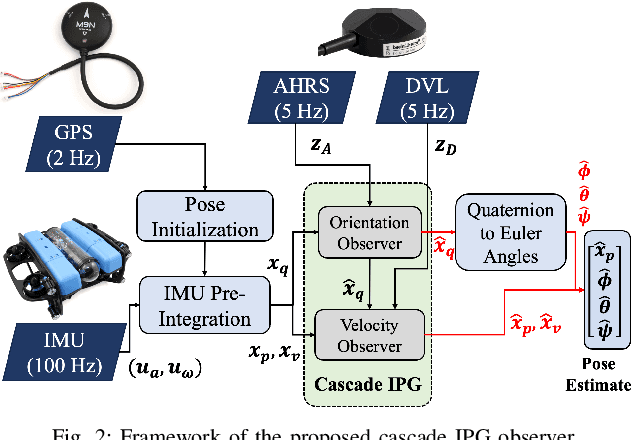
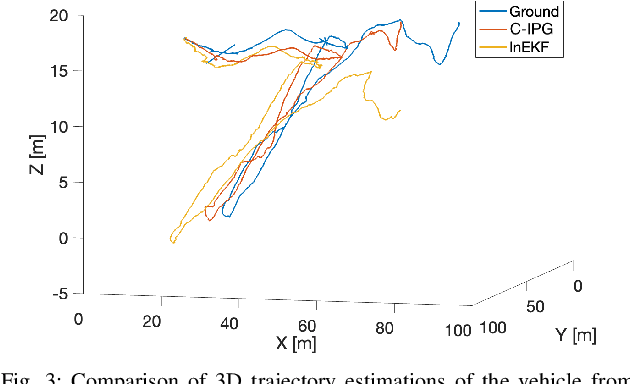

Abstract:This paper presents a novel cascade nonlinear observer framework for inertial state estimation. It tackles the problem of intermediate state estimation when external localization is unavailable or in the event of a sensor outage. The proposed observer comprises two nonlinear observers based on a recently developed iteratively preconditioned gradient descent (IPG) algorithm. It takes the inputs via an IMU preintegration model where the first observer is a quaternion-based IPG. The output for the first observer is the input for the second observer, estimating the velocity and, consequently, the position. The proposed observer is validated on a public underwater dataset and a real-world experiment using our robot platform. The estimation is compared with an extended Kalman filter (EKF) and an invariant extended Kalman filter (InEKF). Results demonstrate that our method outperforms these methods regarding better positional accuracy and lower variance.
3D Water Quality Mapping using Invariant Extended Kalman Filtering for Underwater Robot Localization
Sep 17, 2024Abstract:Water quality mapping for critical parameters such as temperature, salinity, and turbidity is crucial for assessing an aquaculture farm's health and yield capacity. Traditional approaches involve using boats or human divers, which are time-constrained and lack depth variability. This work presents an innovative approach to 3D water quality mapping in shallow water environments using a BlueROV2 equipped with GPS and a water quality sensor. This system allows for accurate location correction by resurfacing when errors occur. This study is being conducted at an oyster farm in the Chesapeake Bay, USA, providing a more comprehensive and precise water quality analysis in aquaculture settings.
Reinforcement Learning Driven Cooperative Ball Balance in Rigidly Coupled Drones
Apr 29, 2024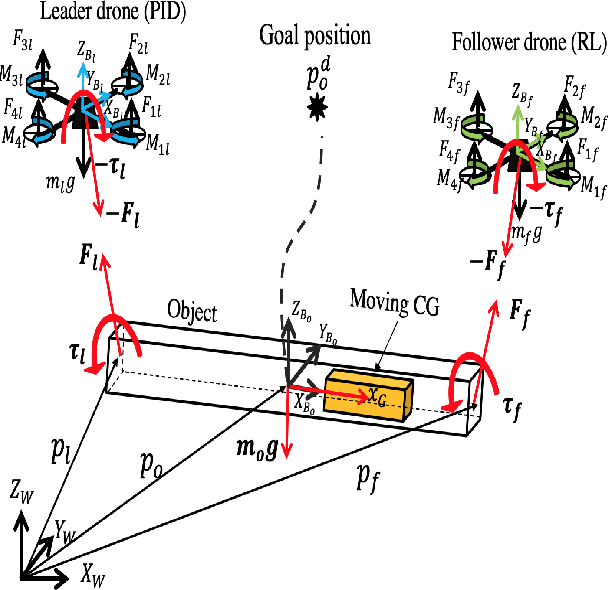
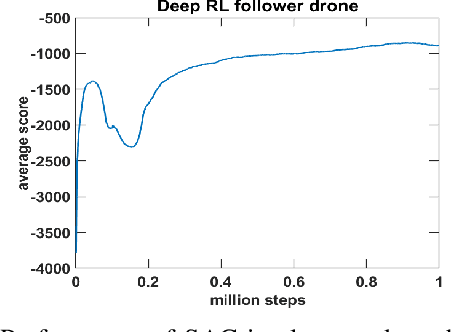
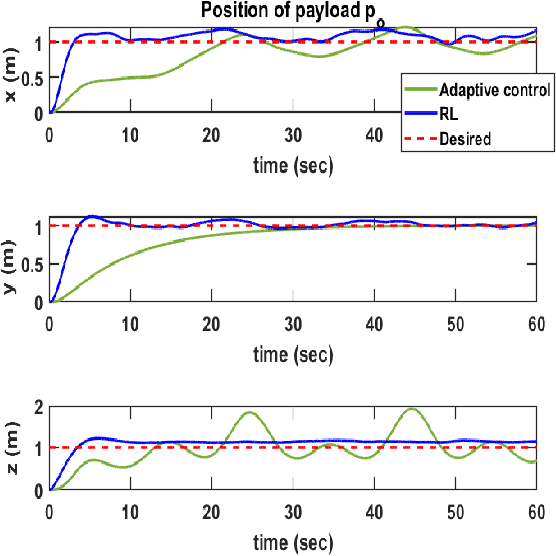
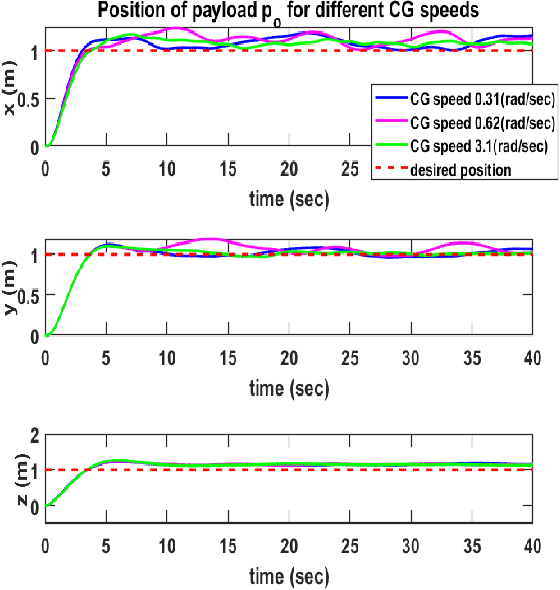
Abstract:Multi-drone cooperative transport (CT) problem has been widely studied in the literature. However, limited work exists on control of such systems in the presence of time-varying uncertainties, such as the time-varying center of gravity (CG). This paper presents a leader-follower approach for the control of a multi-drone CT system with time-varying CG. The leader uses a traditional Proportional-Integral-Derivative (PID) controller, and in contrast, the follower uses a deep reinforcement learning (RL) controller using only local information and minimal leader information. Extensive simulation results are presented, showing the effectiveness of the proposed method over a previously developed adaptive controller and for variations in the mass of the objects being transported and CG speeds. Preliminary experimental work also demonstrates ball balance (depicting moving CG) on a stick/rod lifted by two Crazyflie drones cooperatively.
UIVNAV: Underwater Information-driven Vision-based Navigation via Imitation Learning
Sep 15, 2023Abstract:Autonomous navigation in the underwater environment is challenging due to limited visibility, dynamic changes, and the lack of a cost-efficient accurate localization system. We introduce UIVNav, a novel end-to-end underwater navigation solution designed to drive robots over Objects of Interest (OOI) while avoiding obstacles, without relying on localization. UIVNav uses imitation learning and is inspired by the navigation strategies used by human divers who do not rely on localization. UIVNav consists of the following phases: (1) generating an intermediate representation (IR), and (2) training the navigation policy based on human-labeled IR. By training the navigation policy on IR instead of raw data, the second phase is domain-invariant -- the navigation policy does not need to be retrained if the domain or the OOI changes. We show this by deploying the same navigation policy for surveying two different OOIs, oyster and rock reefs, in two different domains, simulation, and a real pool. We compared our method with complete coverage and random walk methods which showed that our method is more efficient in gathering information for OOIs while also avoiding obstacles. The results show that UIVNav chooses to visit the areas with larger area sizes of oysters or rocks with no prior information about the environment or localization. Moreover, a robot using UIVNav compared to complete coverage method surveys on average 36% more oysters when traveling the same distances. We also demonstrate the feasibility of real-time deployment of UIVNavin pool experiments with BlueROV underwater robot for surveying a bed of oyster shells.
Iteratively Preconditioned Gradient-Descent Approach for Moving Horizon Estimation Problems
Jun 22, 2023


Abstract:Moving horizon estimation (MHE) is a widely studied state estimation approach in several practical applications. In the MHE problem, the state estimates are obtained via the solution of an approximated nonlinear optimization problem. However, this optimization step is known to be computationally complex. Given this limitation, this paper investigates the idea of iteratively preconditioned gradient-descent (IPG) to solve MHE problem with the aim of an improved performance than the existing solution techniques. To our knowledge, the preconditioning technique is used for the first time in this paper to reduce the computational cost and accelerate the crucial optimization step for MHE. The convergence guarantee of the proposed iterative approach for a class of MHE problems is presented. Additionally, sufficient conditions for the MHE problem to be convex are also derived. Finally, the proposed method is implemented on a unicycle localization example. The simulation results demonstrate that the proposed approach can achieve better accuracy with reduced computational costs.
Cartographer_glass: 2D Graph SLAM Framework using LiDAR for Glass Environments
Dec 16, 2022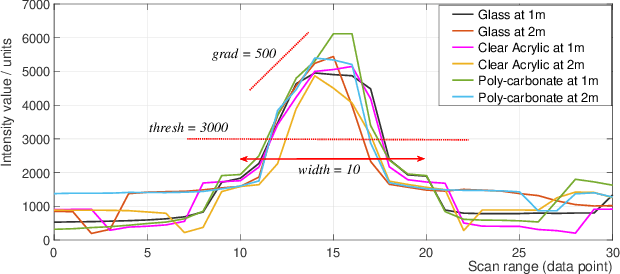
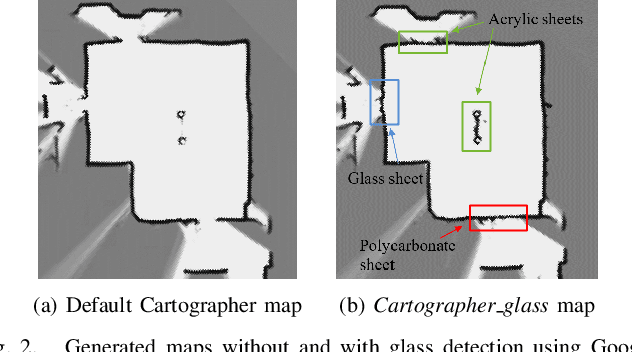
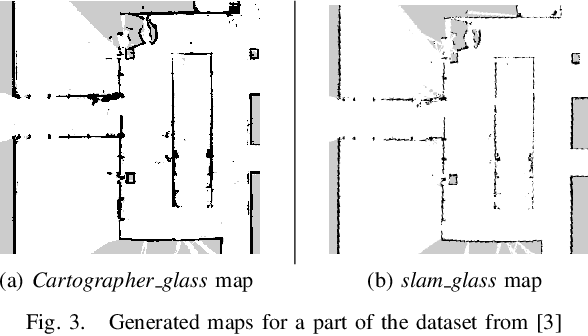
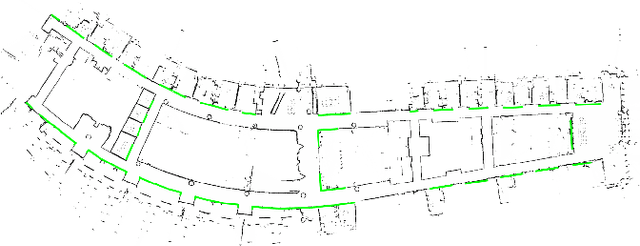
Abstract:We study algorithms for detecting and including glass objects in an optimization-based Simultaneous Localization and Mapping (SLAM) algorithm in this work. When LiDAR data is the primary exteroceptive sensory input, glass objects are not correctly registered. This occurs as the incident light primarily passes through the glass objects or reflects away from the source, resulting in inaccurate range measurements for glass surfaces. Consequently, the localization and mapping performance is impacted, thereby rendering navigation in such environments unreliable. Optimization-based SLAM solutions, which are also referred to as Graph SLAM, are widely regarded as state of the art. In this paper, we utilize a simple and computationally inexpensive glass detection scheme for detecting glass objects and present the methodology to incorporate the identified objects into the occupancy grid maintained by such an algorithm (Google Cartographer). We develop both local (submap level) and global algorithms for achieving the objective mentioned above and compare the maps produced by our method with those produced by an existing algorithm that utilizes particle filter based SLAM.
A Control Theoretic Framework for Adaptive Gradient Optimizers in Machine Learning
Jun 04, 2022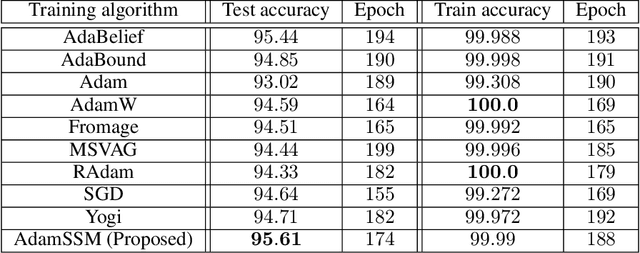

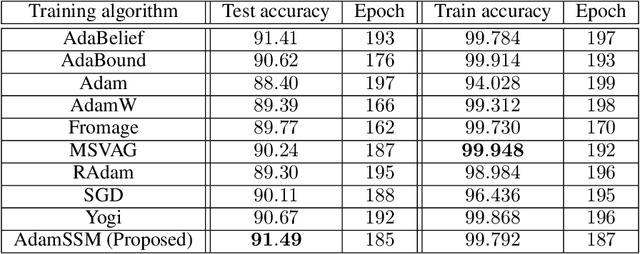
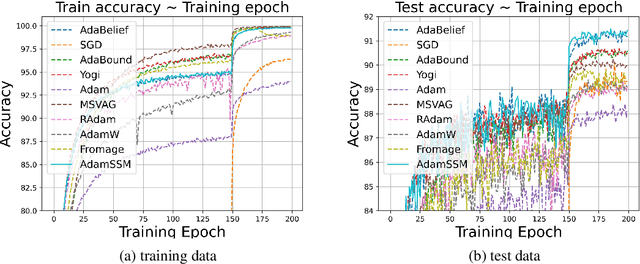
Abstract:Adaptive gradient methods have become popular in optimizing deep neural networks; recent examples include AdaGrad and Adam. Although Adam usually converges faster, variations of Adam, for instance, the AdaBelief algorithm, have been proposed to enhance Adam's poor generalization ability compared to the classical stochastic gradient method. This paper develops a generic framework for adaptive gradient methods that solve non-convex optimization problems. We first model the adaptive gradient methods in a state-space framework, which allows us to present simpler convergence proofs of adaptive optimizers such as AdaGrad, Adam, and AdaBelief. We then utilize the transfer function paradigm from classical control theory to propose a new variant of Adam, coined AdamSSM. We add an appropriate pole-zero pair in the transfer function from squared gradients to the second moment estimate. We prove the convergence of the proposed AdamSSM algorithm. Applications on benchmark machine learning tasks of image classification using CNN architectures and language modeling using LSTM architecture demonstrate that the AdamSSM algorithm improves the gap between generalization accuracy and faster convergence than the recent adaptive gradient methods.
On Accelerating Distributed Convex Optimizations
Aug 19, 2021



Abstract:This paper studies a distributed multi-agent convex optimization problem. The system comprises multiple agents in this problem, each with a set of local data points and an associated local cost function. The agents are connected to a server, and there is no inter-agent communication. The agents' goal is to learn a parameter vector that optimizes the aggregate of their local costs without revealing their local data points. In principle, the agents can solve this problem by collaborating with the server using the traditional distributed gradient-descent method. However, when the aggregate cost is ill-conditioned, the gradient-descent method (i) requires a large number of iterations to converge, and (ii) is highly unstable against process noise. We propose an iterative pre-conditioning technique to mitigate the deleterious effects of the cost function's conditioning on the convergence rate of distributed gradient-descent. Unlike the conventional pre-conditioning techniques, the pre-conditioner matrix in our proposed technique updates iteratively to facilitate implementation on the distributed network. In the distributed setting, we provably show that the proposed algorithm converges linearly with an improved rate of convergence than the traditional and adaptive gradient-descent methods. Additionally, for the special case when the minimizer of the aggregate cost is unique, our algorithm converges superlinearly. We demonstrate our algorithm's superior performance compared to prominent distributed algorithms for solving real logistic regression problems and emulating neural network training via a noisy quadratic model, thereby signifying the proposed algorithm's efficiency for distributively solving non-convex optimization. Moreover, we empirically show that the proposed algorithm results in faster training without compromising the generalization performance.
Generalized AdaGrad and Adam: A State-Space Perspective
May 31, 2021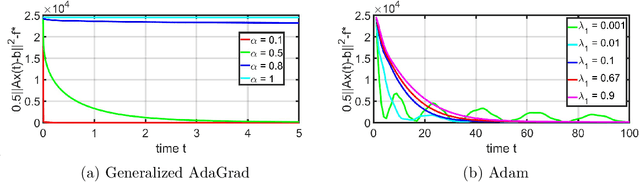
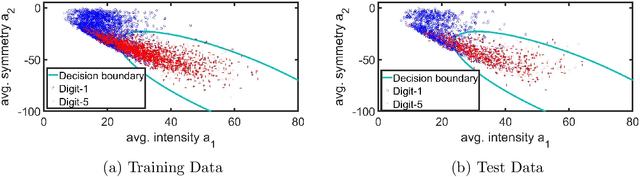
Abstract:Accelerated gradient-based methods are being extensively used for solving non-convex machine learning problems, especially when the data points are abundant or the available data is distributed across several agents. Two of the prominent accelerated gradient algorithms are AdaGrad and Adam. AdaGrad is the simplest accelerated gradient method, which is particularly effective for sparse data. Adam has been shown to perform favorably in deep learning problems compared to other methods. In this paper, we propose a new fast optimizer, Generalized AdaGrad (G-AdaGrad), for accelerating the solution of potentially non-convex machine learning problems. Specifically, we adopt a state-space perspective for analyzing the convergence of gradient acceleration algorithms, namely G-AdaGrad and Adam, in machine learning. Our proposed state-space models are governed by ordinary differential equations. We present simple convergence proofs of these two algorithms in the deterministic settings with minimal assumptions. Our analysis also provides intuition behind improving upon AdaGrad's convergence rate. We provide empirical results on MNIST dataset to reinforce our claims on the convergence and performance of G-AdaGrad and Adam.
Robustness of Iteratively Pre-Conditioned Gradient-Descent Method: The Case of Distributed Linear Regression Problem
Jan 26, 2021


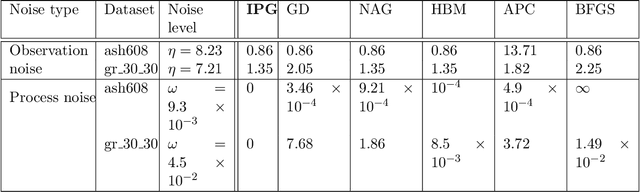
Abstract:This paper considers the problem of multi-agent distributed linear regression in the presence of system noises. In this problem, the system comprises multiple agents wherein each agent locally observes a set of data points, and the agents' goal is to compute a linear model that best fits the collective data points observed by all the agents. We consider a server-based distributed architecture where the agents interact with a common server to solve the problem; however, the server cannot access the agents' data points. We consider a practical scenario wherein the system either has observation noise, i.e., the data points observed by the agents are corrupted, or has process noise, i.e., the computations performed by the server and the agents are corrupted. In noise-free systems, the recently proposed distributed linear regression algorithm, named the Iteratively Pre-conditioned Gradient-descent (IPG) method, has been claimed to converge faster than related methods. In this paper, we study the robustness of the IPG method, against both the observation noise and the process noise. We empirically show that the robustness of the IPG method compares favorably to the state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge