Predicting the Future of AI with AI: High-quality link prediction in an exponentially growing knowledge network

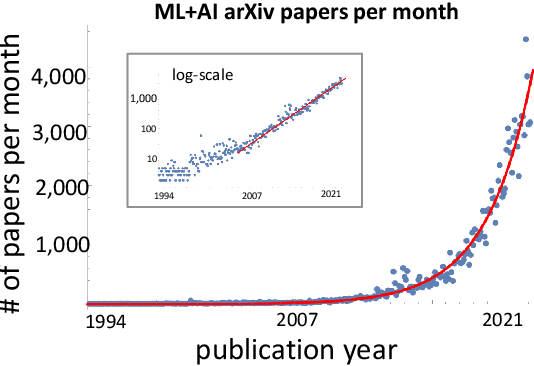
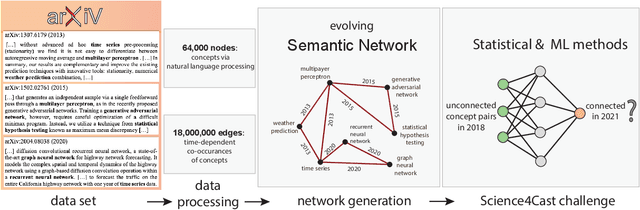
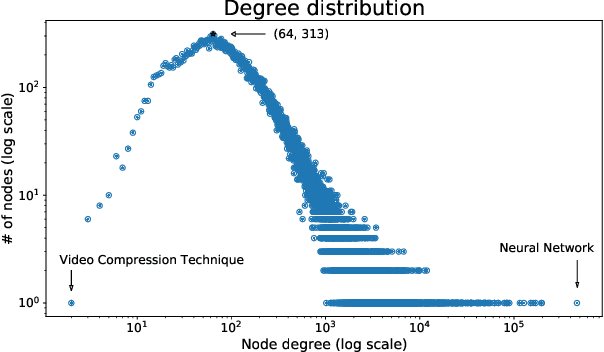
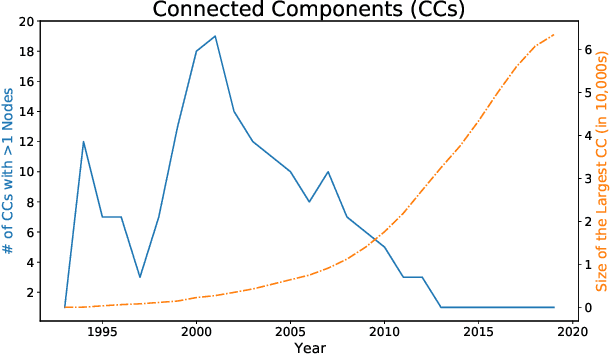
A tool that could suggest new personalized research directions and ideas by taking insights from the scientific literature could significantly accelerate the progress of science. A field that might benefit from such an approach is artificial intelligence (AI) research, where the number of scientific publications has been growing exponentially over the last years, making it challenging for human researchers to keep track of the progress. Here, we use AI techniques to predict the future research directions of AI itself. We develop a new graph-based benchmark based on real-world data -- the Science4Cast benchmark, which aims to predict the future state of an evolving semantic network of AI. For that, we use more than 100,000 research papers and build up a knowledge network with more than 64,000 concept nodes. We then present ten diverse methods to tackle this task, ranging from pure statistical to pure learning methods. Surprisingly, the most powerful methods use a carefully curated set of network features, rather than an end-to-end AI approach. It indicates a great potential that can be unleashed for purely ML approaches without human knowledge. Ultimately, better predictions of new future research directions will be a crucial component of more advanced research suggestion tools.

Improving random walk rankings with feature selection and imputation

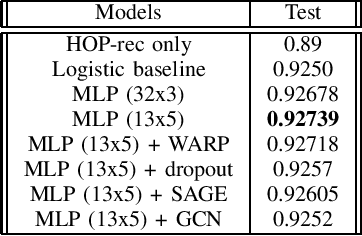
The Science4cast Competition consists of predicting new links in a semantic network, with each node representing a concept and each edge representing a link proposed by a paper relating two concepts. This network contains information from 1994-2017, with a discretization of days (which represents the publication date of the underlying papers). Team Hash Brown's final submission, \emph{ee5a}, achieved a score of 0.92738 on the test set. Our team's score ranks \emph{second place}, 0.01 below the winner's score. This paper details our model, its intuition, and the performance of its variations in the test set.

Minimax Rates for STIT and Poisson Hyperplane Random Forests

In [12], Mourtada, Ga\"{i}ffas and Scornet showed that, under proper tuning of the complexity parameters, random trees and forests built from the Mondrian process in $\mathbb{R}^d$ achieve the minimax rate for $\beta$-H\"{o}lder continuous functions, and random forests achieve the minimax rate for $(1+\beta)$-H\"{o}lder functions in arbitrary dimension, where $\beta \in (0,1]$. In this work, we show that a much larger class of random forests built from random partitions of $\mathbb{R}^d$ also achieve these minimax rates. This class includes STIT random forests, the most general class of random forests built from a self-similar and stationary partition of $\mathbb{R}^d$ by hyperplane cuts possible, as well as forests derived from Poisson hyperplane tessellations. Our proof technique relies on classical results as well as recent advances on stationary random tessellations in stochastic geometry.

Causal Discovery of a River Network from its Extremes

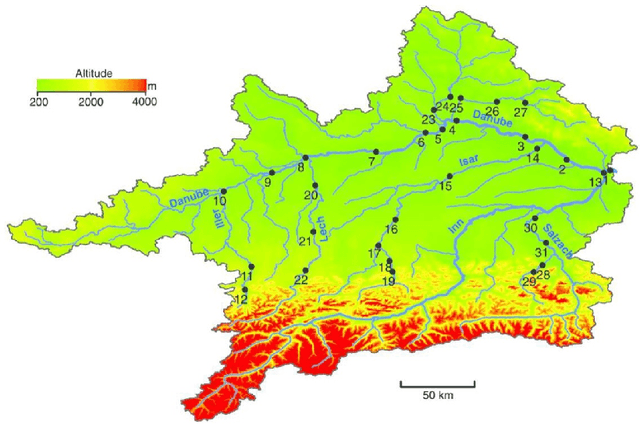
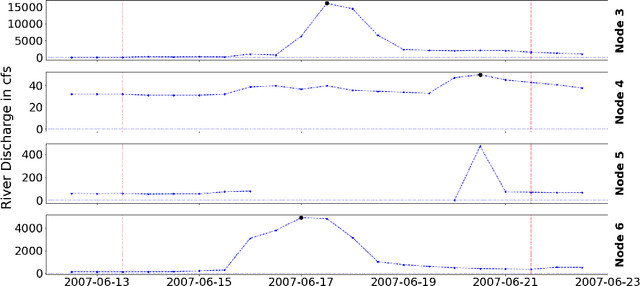
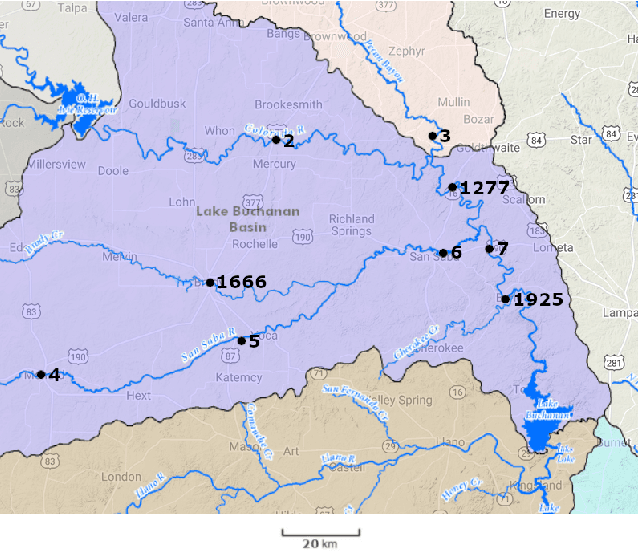
Causal inference for extremes aims to discover cause and effect relations between large observed values of random variables. Over the last years, a number of methods have been proposed for solving the Hidden River Problem, with the Danube data set as benchmark. In this paper, we provide \QTree, a new and simple algorithm to solve the Hidden River Problem that outperforms existing methods. \QTree\ returns a directed graph and achieves almost perfect recovery on the Danube as well as on new data from the Lower Colorado River. It can handle missing data, has an automated parameter tuning procedure, and runs in time $O(n |V|^2)$, where $n$ is the number of observations and $|V|$ the number of nodes in the graph. \QTree\ relies on qualitative aspects of the max-linear Bayesian network model.

Clustering with Fast, Automated and Reproducible assessment applied to longitudinal neural tracking

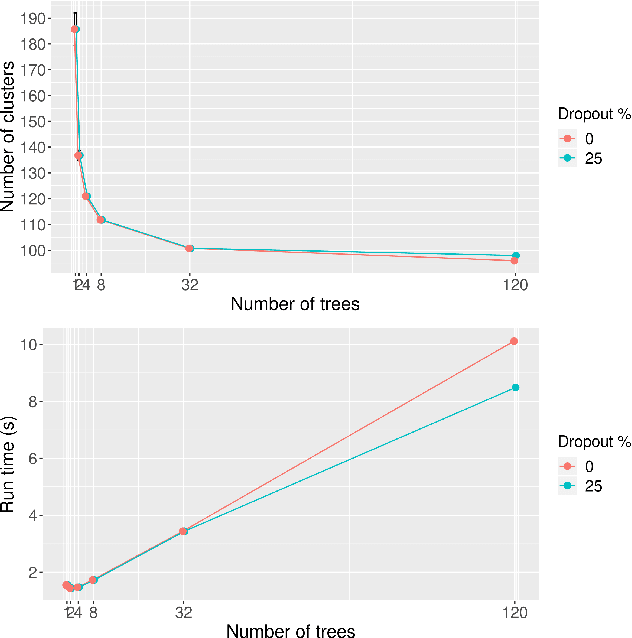
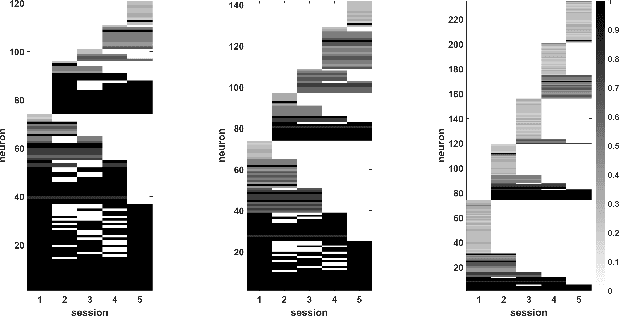
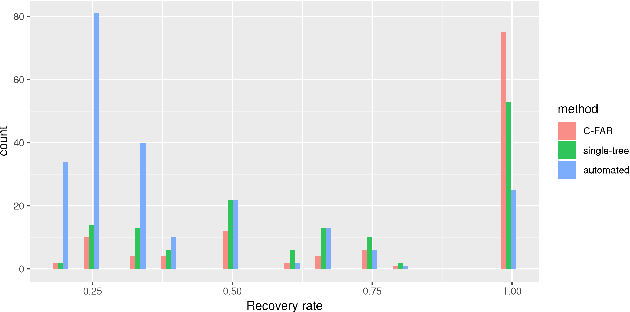
Across many areas, from neural tracking to database entity resolution, manual assessment of clusters by human experts presents a bottleneck in rapid development of scalable and specialized clustering methods. To solve this problem we develop C-FAR, a novel method for Fast, Automated and Reproducible assessment of multiple hierarchical clustering algorithms simultaneously. Our algorithm takes any number of hierarchical clustering trees as input, then strategically queries pairs for human feedback, and outputs an optimal clustering among those nominated by these trees. While it is applicable to large dataset in any domain that utilizes pairwise comparisons for assessment, our flagship application is the cluster aggregation step in spike-sorting, the task of assigning waveforms (spikes) in recordings to neurons. On simulated data of 96 neurons under adverse conditions, including drifting and 25\% blackout, our algorithm produces near-perfect tracking relative to the ground truth. Our runtime scales linearly in the number of input trees, making it a competitive computational tool. These results indicate that C-FAR is highly suitable as a model selection and assessment tool in clustering tasks.

Classification on Large Networks: A Quantitative Bound via Motifs and Graphons

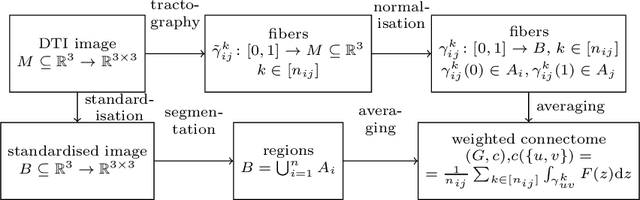
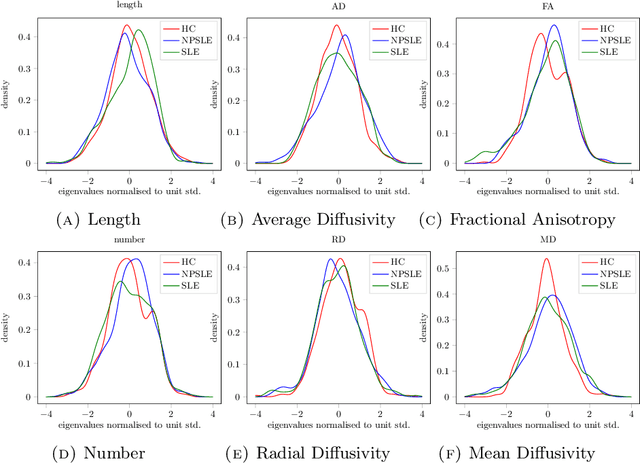
When each data point is a large graph, graph statistics such as densities of certain subgraphs (motifs) can be used as feature vectors for machine learning. While intuitive, motif counts are expensive to compute and difficult to work with theoretically. Via graphon theory, we give an explicit quantitative bound for the ability of motif homomorphisms to distinguish large networks under both generative and sampling noise. Furthermore, we give similar bounds for the graph spectrum and connect it to homomorphism densities of cycles. This results in an easily computable classifier on graph data with theoretical performance guarantee. Our method yields competitive results on classification tasks for the autoimmune disease Lupus Erythematosus.