Causal Discovery of a River Network from its Extremes
Paper and Code
Feb 11, 2021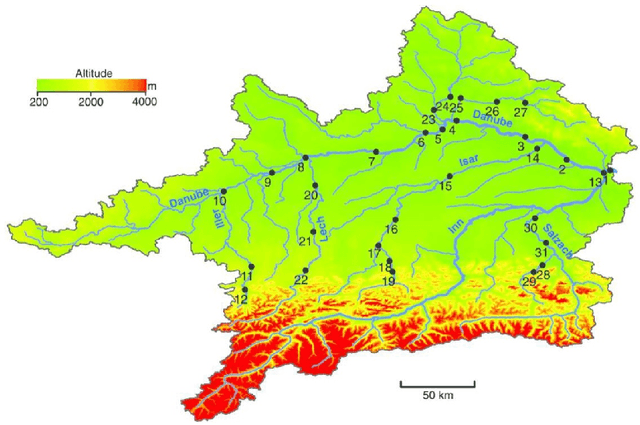
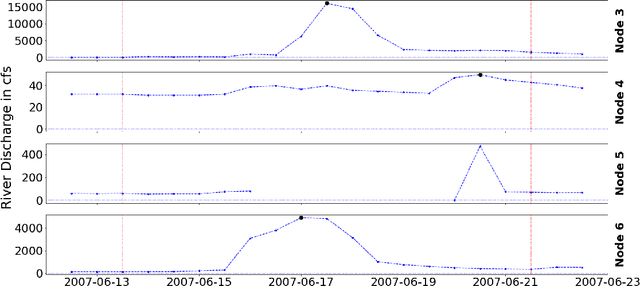
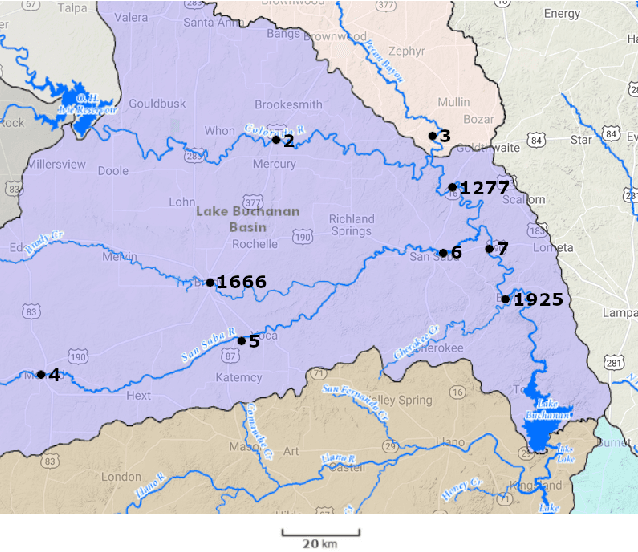

Causal inference for extremes aims to discover cause and effect relations between large observed values of random variables. Over the last years, a number of methods have been proposed for solving the Hidden River Problem, with the Danube data set as benchmark. In this paper, we provide \QTree, a new and simple algorithm to solve the Hidden River Problem that outperforms existing methods. \QTree\ returns a directed graph and achieves almost perfect recovery on the Danube as well as on new data from the Lower Colorado River. It can handle missing data, has an automated parameter tuning procedure, and runs in time $O(n |V|^2)$, where $n$ is the number of observations and $|V|$ the number of nodes in the graph. \QTree\ relies on qualitative aspects of the max-linear Bayesian network model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge