SPOTR: Spatio-temporal Pooling One-Token Reconstruction for Universal Physiological Signal Self-supervised Learning

Physiological signals such as EEG, ECG, and PPG are widely used in clinical monitoring. Recent self-supervised learning (SSL) methods offer an attractive way to leverage unlabeled recordings, yet they still fall short in practice. In particular, current SSL methods struggle across heterogeneous datasets, often distorting clinically meaningful structures or learning shortcuts from temporal and cross-channel redundancy. Consequently, existing SSL methods often deliver limited performance under linear probing, a lightweight adaptation setting that better matches real-world medical scenarios. Moreover, most Transformer-based SSL models encode a flattened spatiotemporal token sequence, incurring high computation and memory cost, and are typically developed within a single modality. To address these limitations, we present SPOTR (Spatio-temporal Pooling One-Token Reconstruction), a compress-reconstruct pretraining framework that introduces a single-token global bottleneck for physiological signals. SPOTR compresses each waveform into a single-token representation and reconstructs the signal conditioned only on this representation. Meanwhile, SPOTR introduces an efficient spatio-temporal compaction module to reduce computation and memory cost. Pretrained on 20 datasets spanning EEG, iEEG, ECG, and PPG, SPOTR consistently outperforms the strongest baseline under linear probing, improving average AUC by 18.49%, 21.71%, 17.86%, and 4.64%, respectively. Compared with a representative general-purpose time-series foundation model, SPOTR achieves around 78% lower latency and 52% lower peak GPU memory on average. The code can be found at https://github.com/5GYYYYY/SPOTR.

MedTS-TTT: Test-Time Training for Medical Time Series Classification

Medical time series (MedTS) signals such as electroencephalography (EEG) and electrocardiography (ECG) support many clinical applications. However, substantial subject-level heterogeneity often induces subject-level distribution shift, causing a fixed parameter set to generalize poorly to unseen individuals. Compared with domain adaptation methods that often depend on extra adaptation components or target-batch statistics, Test-Time Training (TTT) provides a more practical solution for sequential clinical data by enabling online adaptation from unlabeled test samples. However, many representative TTT methods require iterative inner-loop optimization, increasing test-time overhead. In this paper, we propose MedTS-TTT, a test-time training framework for medical time series modeling. MedTS-TTT is built upon Closed-Loop Self-Alignment Test-Time Training (CLSA-TTT) and a Gated Convolutional Backbone (GCB). CLSA-TTT constructs a token-level self-supervised target and performs a single-step fast-weight update for intra-layer closed-loop alignment, enabling rapid sample-wise adaptation without iterative inner-loop optimization. GCB combines CLSA-TTT-based fast adaptation and token-level fusion with a gated convolutional branch to balance local dynamic modeling and information-flow control. On 4 public datasets (2 EEG and 2 ECG) with subject-independent splits, MedTS-TTT achieves 11 top-1 rankings out of 12 evaluations across 9 baselines and 3 metrics. The code is publicly available at https://github.com/mingzhi-c/MedTS-TTT.

Stronger Normalization-Free Transformers

Although normalization layers have long been viewed as indispensable components of deep learning architectures, the recent introduction of Dynamic Tanh (DyT) has demonstrated that alternatives are possible. The point-wise function DyT constrains extreme values for stable convergence and reaches normalization-level performance; this work seeks further for function designs that can surpass it. We first study how the intrinsic properties of point-wise functions influence training and performance. Building on these findings, we conduct a large-scale search for a more effective function design. Through this exploration, we introduce $\mathrm{Derf}(x) = \mathrm{erf}(αx + s)$, where $\mathrm{erf}(x)$ is the rescaled Gaussian cumulative distribution function, and identify it as the most performant design. Derf outperforms LayerNorm, RMSNorm, and DyT across a wide range of domains, including vision (image recognition and generation), speech representation, and DNA sequence modeling. Our findings suggest that the performance gains of Derf largely stem from its improved generalization rather than stronger fitting capacity. Its simplicity and stronger performance make Derf a practical choice for normalization-free Transformer architectures.

Federated Learning for Medical Image Classification: A Comprehensive Benchmark

The federated learning paradigm is wellsuited for the field of medical image analysis, as it can effectively cope with machine learning on isolated multicenter data while protecting the privacy of participating parties. However, current research on optimization algorithms in federated learning often focuses on limited datasets and scenarios, primarily centered around natural images, with insufficient comparative experiments in medical contexts. In this work, we conduct a comprehensive evaluation of several state-of-the-art federated learning algorithms in the context of medical imaging. We conduct a fair comparison of classification models trained using various federated learning algorithms across multiple medical imaging datasets. Additionally, we evaluate system performance metrics, such as communication cost and computational efficiency, while considering different federated learning architectures. Our findings show that medical imaging datasets pose substantial challenges for current federated learning optimization algorithms. No single algorithm consistently delivers optimal performance across all medical federated learning scenarios, and many optimization algorithms may underperform when applied to these datasets. Our experiments provide a benchmark and guidance for future research and application of federated learning in medical imaging contexts. Furthermore, we propose an efficient and robust method that combines generative techniques using denoising diffusion probabilistic models with label smoothing to augment datasets, widely enhancing the performance of federated learning on classification tasks across various medical imaging datasets. Our code will be released on GitHub, offering a reliable and comprehensive benchmark for future federated learning studies in medical imaging.

MIGA: Mutual Information-Guided Attack on Denoising Models for Semantic Manipulation

Deep learning-based denoising models have been widely employed in vision tasks, functioning as filters to eliminate noise while retaining crucial semantic information. Additionally, they play a vital role in defending against adversarial perturbations that threaten downstream tasks. However, these models can be intrinsically susceptible to adversarial attacks due to their dependence on specific noise assumptions. Existing attacks on denoising models mainly aim at deteriorating visual clarity while neglecting semantic manipulation, rendering them either easily detectable or limited in effectiveness. In this paper, we propose Mutual Information-Guided Attack (MIGA), the first method designed to directly attack deep denoising models by strategically disrupting their ability to preserve semantic content via adversarial perturbations. By minimizing the mutual information between the original and denoised images, a measure of semantic similarity. MIGA forces the denoiser to produce perceptually clean yet semantically altered outputs. While these images appear visually plausible, they encode systematically distorted semantics, revealing a fundamental vulnerability in denoising models. These distortions persist in denoised outputs and can be quantitatively assessed through downstream task performance. We propose new evaluation metrics and systematically assess MIGA on four denoising models across five datasets, demonstrating its consistent effectiveness in disrupting semantic fidelity. Our findings suggest that denoising models are not always robust and can introduce security risks in real-world applications.

Improving EEG Classification Through Randomly Reassembling Original and Generated Data with Transformer-based Diffusion Models

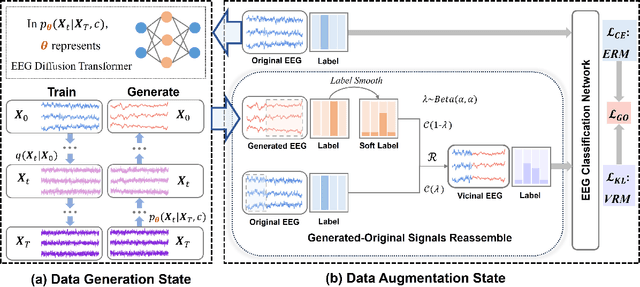
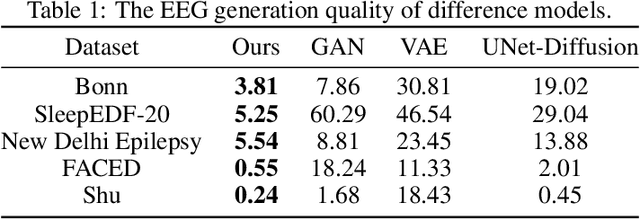
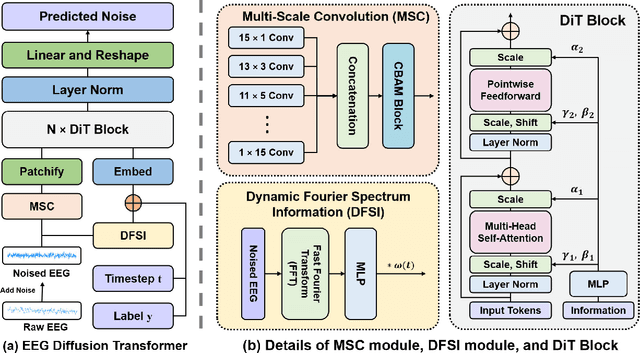
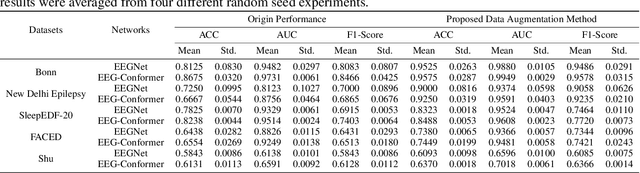
Electroencephalogram (EEG) classification has been widely used in various medical and engineering applications, where it is important for understanding brain function, diagnosing diseases, and assessing mental health conditions. However, the scarcity of EEG data severely restricts the performance of EEG classification networks, and generative model-based data augmentation methods emerging as potential solutions to overcome this challenge. There are two problems with existing such methods: (1) The quality of the generated EEG signals is not high. (2) The enhancement of EEG classification networks is not effective. In this paper, we propose a Transformer-based denoising diffusion probabilistic model and a generated data-based data augmentation method to address the above two problems. For the characteristics of EEG signals, we propose a constant-factor scaling method to preprocess the signals, which reduces the loss of information. We incorporated Multi-Scale Convolution and Dynamic Fourier Spectrum Information modules into the model, improving the stability of the training process and the quality of the generated data. The proposed augmentation method randomly reassemble the generated data with original data in the time-domain to obtain vicinal data, which improves the model performance by minimizing the empirical risk and the vicinal risk. We experiment the proposed augmentation method on five EEG datasets for four tasks and observe significant accuracy performance improvements: 14.00% on the Bonn dataset; 25.83% on the New Delhi epilepsy dataset; 4.98% on the SleepEDF-20 dataset; 9.42% on the FACED dataset; 2.5% on the Shu dataset. We intend to make the code of our method publicly accessible shortly

Spectral Clustering with Smooth Tiny Clusters

Spectral clustering is one of the most prominent clustering approaches. The distance-based similarity is the most widely used method for spectral clustering. However, people have already noticed that this is not suitable for multi-scale data, as the distance varies a lot for clusters with different densities. State of the art(ROSC and CAST ) addresses this limitation by taking the reachability similarity of objects into account. However, we observe that in real-world scenarios, data in the same cluster tend to present in a smooth manner, and previous algorithms never take this into account. Based on this observation, we propose a novel clustering algorithm, which con-siders the smoothness of data for the first time. We first divide objects into a great many tiny clusters. Our key idea is to cluster tiny clusters, whose centers constitute smooth graphs. Theoretical analysis and experimental results show that our clustering algorithm significantly outperforms state of the art. Although in this paper, we singly focus on multi-scale situations, the idea of data smoothness can certainly be extended to any clustering algorithms