Detecting Violations of Differential Privacy for Quantum Algorithms

Quantum algorithms for solving a wide range of practical problems have been proposed in the last ten years, such as data search and analysis, product recommendation, and credit scoring. The concern about privacy and other ethical issues in quantum computing naturally rises up. In this paper, we define a formal framework for detecting violations of differential privacy for quantum algorithms. A detection algorithm is developed to verify whether a (noisy) quantum algorithm is differentially private and automatically generate bugging information when the violation of differential privacy is reported. The information consists of a pair of quantum states that violate the privacy, to illustrate the cause of the violation. Our algorithm is equipped with Tensor Networks, a highly efficient data structure, and executed both on TensorFlow Quantum and TorchQuantum which are the quantum extensions of famous machine learning platforms -- TensorFlow and PyTorch, respectively. The effectiveness and efficiency of our algorithm are confirmed by the experimental results of almost all types of quantum algorithms already implemented on realistic quantum computers, including quantum supremacy algorithms (beyond the capability of classical algorithms), quantum machine learning models, quantum approximate optimization algorithms, and variational quantum eigensolvers with up to 21 quantum bits.

Differentiable Quantum Programming with Unbounded Loops

The emergence of variational quantum applications has led to the development of automatic differentiation techniques in quantum computing. Recently, Zhu et al. (PLDI 2020) have formulated differentiable quantum programming with bounded loops, providing a framework for scalable gradient calculation by quantum means for training quantum variational applications. However, promising parameterized quantum applications, e.g., quantum walk and unitary implementation, cannot be trained in the existing framework due to the natural involvement of unbounded loops. To fill in the gap, we provide the first differentiable quantum programming framework with unbounded loops, including a newly designed differentiation rule, code transformation, and their correctness proof. Technically, we introduce a randomized estimator for derivatives to deal with the infinite sum in the differentiation of unbounded loops, whose applicability in classical and probabilistic programming is also discussed. We implement our framework with Python and Q#, and demonstrate a reasonable sample efficiency. Through extensive case studies, we showcase an exciting application of our framework in automatically identifying close-to-optimal parameters for several parameterized quantum applications.

Verifying Fairness in Quantum Machine Learning

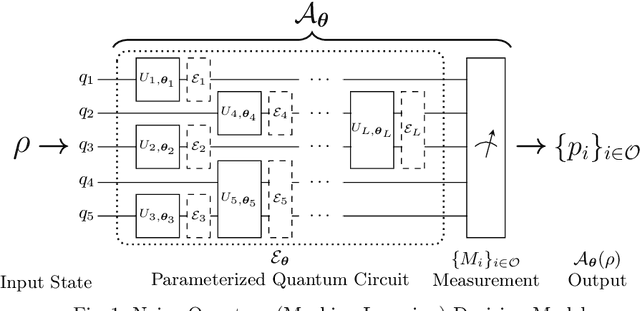
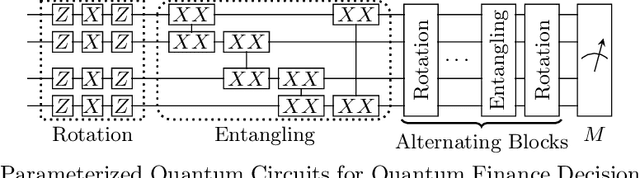
Due to the beyond-classical capability of quantum computing, quantum machine learning is applied independently or embedded in classical models for decision making, especially in the field of finance. Fairness and other ethical issues are often one of the main concerns in decision making. In this work, we define a formal framework for the fairness verification and analysis of quantum machine learning decision models, where we adopt one of the most popular notions of fairness in the literature based on the intuition -- any two similar individuals must be treated similarly and are thus unbiased. We show that quantum noise can improve fairness and develop an algorithm to check whether a (noisy) quantum machine learning model is fair. In particular, this algorithm can find bias kernels of quantum data (encoding individuals) during checking. These bias kernels generate infinitely many bias pairs for investigating the unfairness of the model. Our algorithm is designed based on a highly efficient data structure -- Tensor Networks -- and implemented on Google's TensorFlow Quantum. The utility and effectiveness of our algorithm are confirmed by the experimental results, including income prediction and credit scoring on real-world data, for a class of random (noisy) quantum decision models with 27 qubits ($2^{27}$-dimensional state space) tripling ($2^{18}$ times more than) that of the state-of-the-art algorithms for verifying quantum machine learning models.

Robustness Verification of Quantum Machine Learning

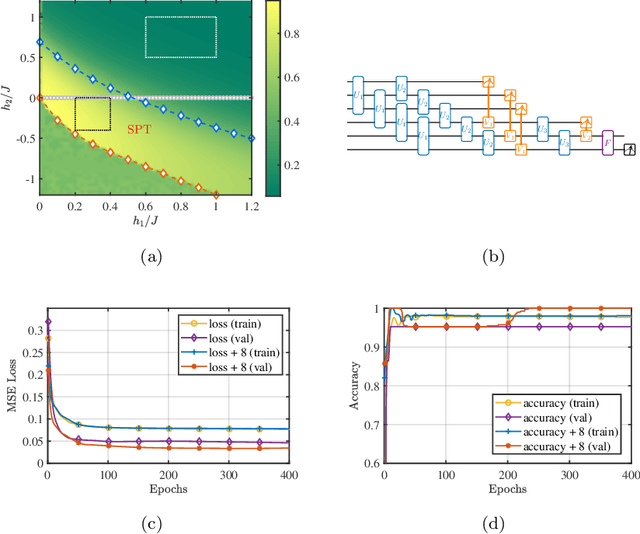
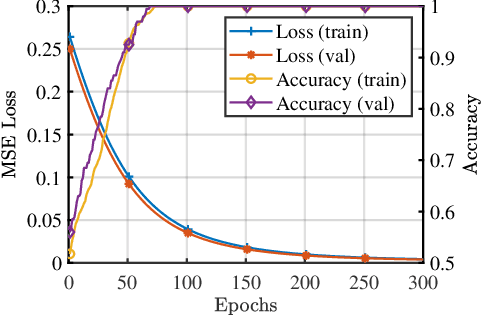
Several important models of machine learning algorithms have been successfully generalized to the quantum world, with potential applications to data analytics in quantum physics that can be implemented on the near future quantum computers. However, noise and decoherence are two major obstacles to the practical implementation of quantum machine learning. In this work, we introduce a general framework for the robustness analysis of quantum machine learning algorithms against noise and decoherence. We argue that fidelity is the only pick of measuring the robustness. A robust bound is derived and an algorithm is developed to check whether or not a quantum machine learning algorithm is robust with respect to the training data. In particular, this algorithm can help to defense attacks and improve the accuracy as it can identify useful new training data during checking. The effectiveness of our robust bound and algorithm is confirmed by the case study of quantum phase recognition. Furthermore, this experiment demonstrates a trade-off between the accuracy of quantum machine learning algorithms and their robustness.

Poq: Projection-based Runtime Assertions for Debugging on a Quantum Computer

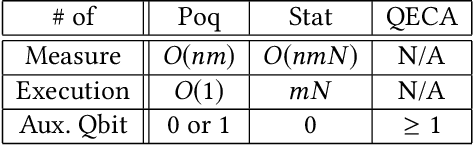
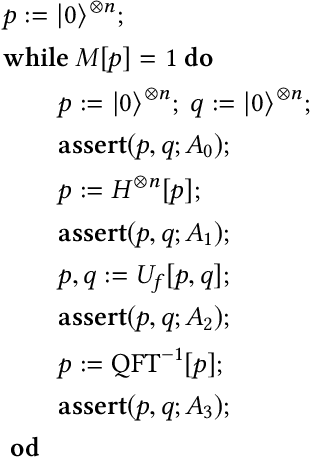
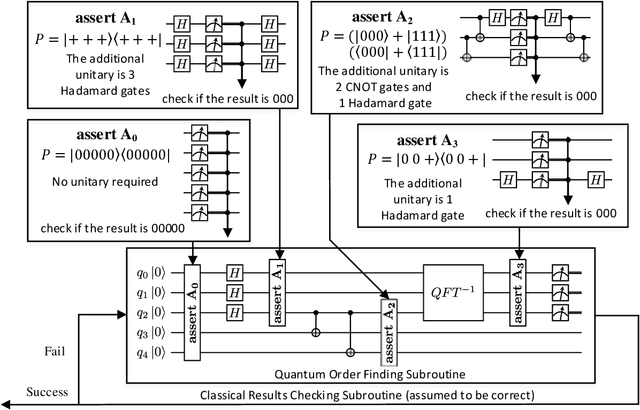
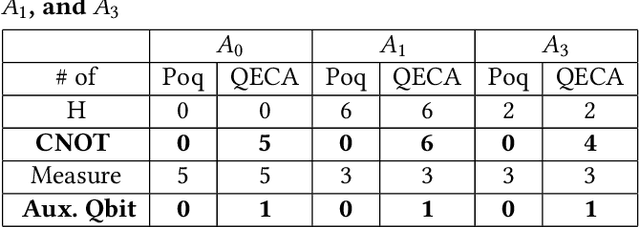
In this paper, we propose Poq, a runtime assertion scheme for debugging on a quantum computer. The predicates in the assertions are represented by projections (or equivalently, closed subspaces of the state space), following Birkhoff-von Neumann quantum logic. The satisfaction of a projection by a quantum state can be directly checked upon a small number of projective measurements rather than a large number of repeated executions. Several techniques are introduced to rotate the predicates to the computational basis, on which a realistic quantum computer usually supports its measurements, so that a satisfying tested state will not be destroyed when an assertion is checked and multi-assertion per testing execution is enabled. We compare Poq with existing quantum program assertions and demonstrate the effectiveness and efficiency of Poq by its applications to assert two sophisticated quantum algorithms.

Quantum Privacy-Preserving Perceptron

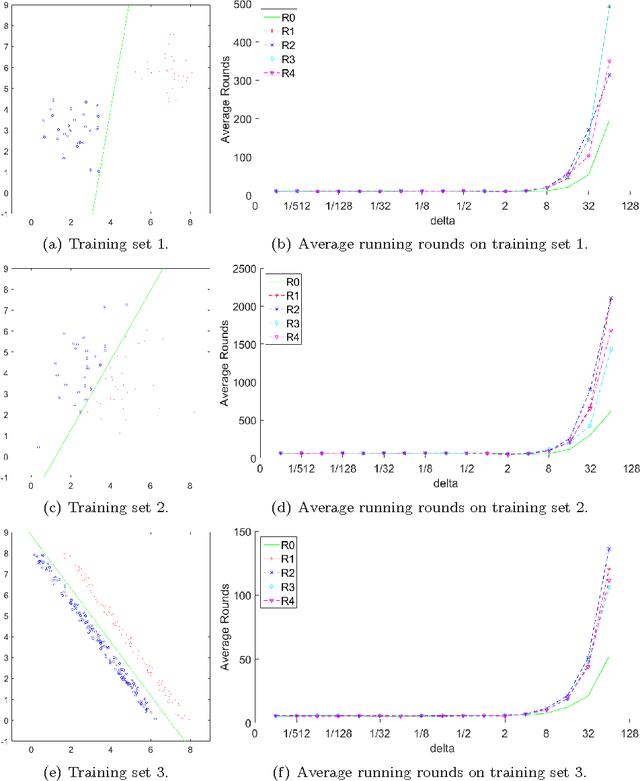
With the extensive applications of machine learning, the issue of private or sensitive data in the training examples becomes more and more serious: during the training process, personal information or habits may be disclosed to unexpected persons or organisations, which can cause serious privacy problems or even financial loss. In this paper, we present a quantum privacy-preserving algorithm for machine learning with perceptron. There are mainly two steps to protect original training examples. Firstly when checking the current classifier, quantum tests are employed to detect data user's possible dishonesty. Secondly when updating the current classifier, private random noise is used to protect the original data. The advantages of our algorithm are: (1) it protects training examples better than the known classical methods; (2) it requires no quantum database and thus is easy to implement.

Quantum Privacy-Preserving Data Mining

Data mining is a key technology in big data analytics and it can discover understandable knowledge (patterns) hidden in large data sets. Association rule is one of the most useful knowledge patterns, and a large number of algorithms have been developed in the data mining literature to generate association rules corresponding to different problems and situations. Privacy becomes a vital issue when data mining is used to sensitive data sets like medical records, commercial data sets and national security. In this Letter, we present a quantum protocol for mining association rules on vertically partitioned databases. The quantum protocol can improve the privacy level preserved by known classical protocols and at the same time it can exponentially reduce the computational complexity and communication cost.

Reasoning about Cardinal Directions between Extended Objects

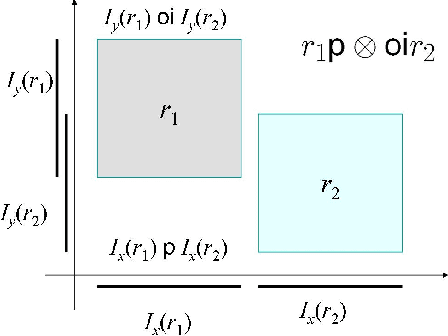
Direction relations between extended spatial objects are important commonsense knowledge. Recently, Goyal and Egenhofer proposed a formal model, known as Cardinal Direction Calculus (CDC), for representing direction relations between connected plane regions. CDC is perhaps the most expressive qualitative calculus for directional information, and has attracted increasing interest from areas such as artificial intelligence, geographical information science, and image retrieval. Given a network of CDC constraints, the consistency problem is deciding if the network is realizable by connected regions in the real plane. This paper provides a cubic algorithm for checking consistency of basic CDC constraint networks, and proves that reasoning with CDC is in general an NP-Complete problem. For a consistent network of basic CDC constraints, our algorithm also returns a 'canonical' solution in cubic time. This cubic algorithm is also adapted to cope with cardinal directions between possibly disconnected regions, in which case currently the best algorithm is of time complexity O(n^5).

Soft constraint abstraction based on semiring homomorphism

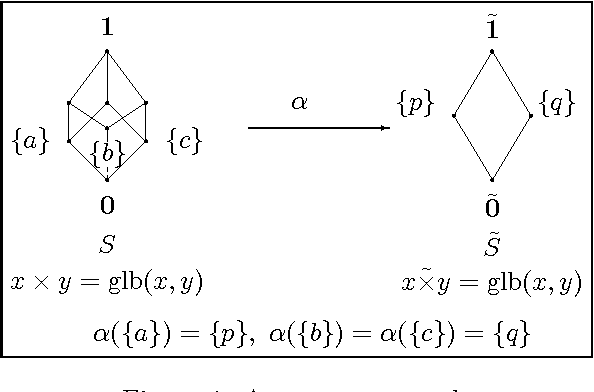
The semiring-based constraint satisfaction problems (semiring CSPs), proposed by Bistarelli, Montanari and Rossi \cite{BMR97}, is a very general framework of soft constraints. In this paper we propose an abstraction scheme for soft constraints that uses semiring homomorphism. To find optimal solutions of the concrete problem, the idea is, first working in the abstract problem and finding its optimal solutions, then using them to solve the concrete problem. In particular, we show that a mapping preserves optimal solutions if and only if it is an order-reflecting semiring homomorphism. Moreover, for a semiring homomorphism $\alpha$ and a problem $P$ over $S$, if $t$ is optimal in $\alpha(P)$, then there is an optimal solution $\bar{t}$ of $P$ such that $\bar{t}$ has the same value as $t$ in $\alpha(P)$.

Retraction and Generalized Extension of Computing with Words

Fuzzy automata, whose input alphabet is a set of numbers or symbols, are a formal model of computing with values. Motivated by Zadeh's paradigm of computing with words rather than numbers, Ying proposed a kind of fuzzy automata, whose input alphabet consists of all fuzzy subsets of a set of symbols, as a formal model of computing with all words. In this paper, we introduce a somewhat general formal model of computing with (some special) words. The new features of the model are that the input alphabet only comprises some (not necessarily all) fuzzy subsets of a set of symbols and the fuzzy transition function can be specified arbitrarily. By employing the methodology of fuzzy control, we establish a retraction principle from computing with words to computing with values for handling crisp inputs and a generalized extension principle from computing with words to computing with all words for handling fuzzy inputs. These principles show that computing with values and computing with all words can be respectively implemented by computing with words. Some algebraic properties of retractions and generalized extensions are addressed as well.