Verifying Fairness in Quantum Machine Learning
Paper and Code
Jul 22, 2022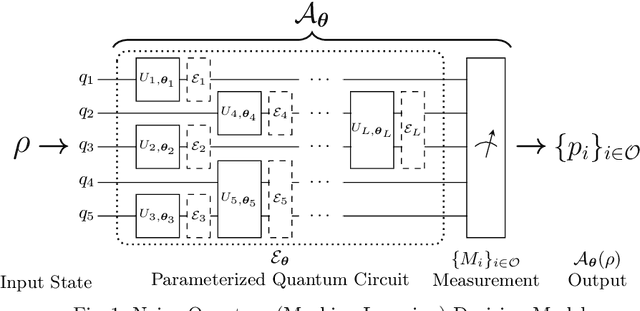

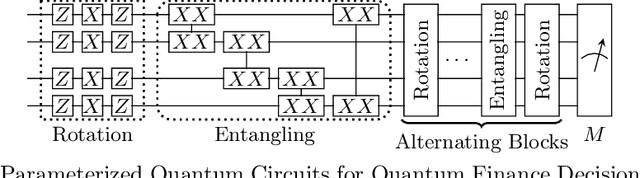

Due to the beyond-classical capability of quantum computing, quantum machine learning is applied independently or embedded in classical models for decision making, especially in the field of finance. Fairness and other ethical issues are often one of the main concerns in decision making. In this work, we define a formal framework for the fairness verification and analysis of quantum machine learning decision models, where we adopt one of the most popular notions of fairness in the literature based on the intuition -- any two similar individuals must be treated similarly and are thus unbiased. We show that quantum noise can improve fairness and develop an algorithm to check whether a (noisy) quantum machine learning model is fair. In particular, this algorithm can find bias kernels of quantum data (encoding individuals) during checking. These bias kernels generate infinitely many bias pairs for investigating the unfairness of the model. Our algorithm is designed based on a highly efficient data structure -- Tensor Networks -- and implemented on Google's TensorFlow Quantum. The utility and effectiveness of our algorithm are confirmed by the experimental results, including income prediction and credit scoring on real-world data, for a class of random (noisy) quantum decision models with 27 qubits ($2^{27}$-dimensional state space) tripling ($2^{18}$ times more than) that of the state-of-the-art algorithms for verifying quantum machine learning models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge