Detecting Violations of Differential Privacy for Quantum Algorithms

Quantum algorithms for solving a wide range of practical problems have been proposed in the last ten years, such as data search and analysis, product recommendation, and credit scoring. The concern about privacy and other ethical issues in quantum computing naturally rises up. In this paper, we define a formal framework for detecting violations of differential privacy for quantum algorithms. A detection algorithm is developed to verify whether a (noisy) quantum algorithm is differentially private and automatically generate bugging information when the violation of differential privacy is reported. The information consists of a pair of quantum states that violate the privacy, to illustrate the cause of the violation. Our algorithm is equipped with Tensor Networks, a highly efficient data structure, and executed both on TensorFlow Quantum and TorchQuantum which are the quantum extensions of famous machine learning platforms -- TensorFlow and PyTorch, respectively. The effectiveness and efficiency of our algorithm are confirmed by the experimental results of almost all types of quantum algorithms already implemented on realistic quantum computers, including quantum supremacy algorithms (beyond the capability of classical algorithms), quantum machine learning models, quantum approximate optimization algorithms, and variational quantum eigensolvers with up to 21 quantum bits.

Differentiable Quantum Programming with Unbounded Loops

The emergence of variational quantum applications has led to the development of automatic differentiation techniques in quantum computing. Recently, Zhu et al. (PLDI 2020) have formulated differentiable quantum programming with bounded loops, providing a framework for scalable gradient calculation by quantum means for training quantum variational applications. However, promising parameterized quantum applications, e.g., quantum walk and unitary implementation, cannot be trained in the existing framework due to the natural involvement of unbounded loops. To fill in the gap, we provide the first differentiable quantum programming framework with unbounded loops, including a newly designed differentiation rule, code transformation, and their correctness proof. Technically, we introduce a randomized estimator for derivatives to deal with the infinite sum in the differentiation of unbounded loops, whose applicability in classical and probabilistic programming is also discussed. We implement our framework with Python and Q#, and demonstrate a reasonable sample efficiency. Through extensive case studies, we showcase an exciting application of our framework in automatically identifying close-to-optimal parameters for several parameterized quantum applications.

Verifying Fairness in Quantum Machine Learning

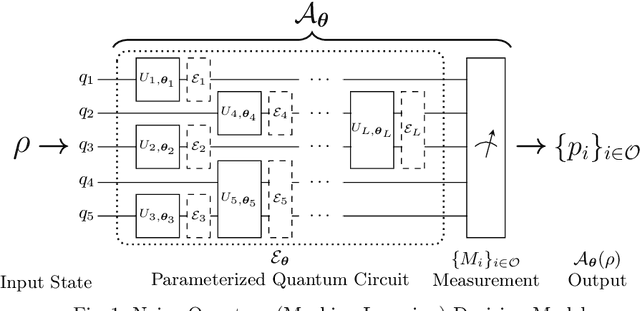
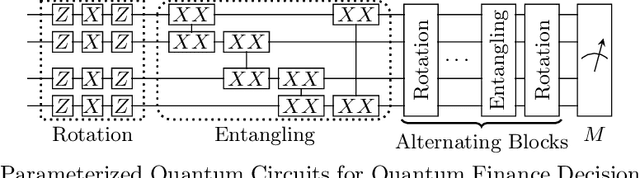
Due to the beyond-classical capability of quantum computing, quantum machine learning is applied independently or embedded in classical models for decision making, especially in the field of finance. Fairness and other ethical issues are often one of the main concerns in decision making. In this work, we define a formal framework for the fairness verification and analysis of quantum machine learning decision models, where we adopt one of the most popular notions of fairness in the literature based on the intuition -- any two similar individuals must be treated similarly and are thus unbiased. We show that quantum noise can improve fairness and develop an algorithm to check whether a (noisy) quantum machine learning model is fair. In particular, this algorithm can find bias kernels of quantum data (encoding individuals) during checking. These bias kernels generate infinitely many bias pairs for investigating the unfairness of the model. Our algorithm is designed based on a highly efficient data structure -- Tensor Networks -- and implemented on Google's TensorFlow Quantum. The utility and effectiveness of our algorithm are confirmed by the experimental results, including income prediction and credit scoring on real-world data, for a class of random (noisy) quantum decision models with 27 qubits ($2^{27}$-dimensional state space) tripling ($2^{18}$ times more than) that of the state-of-the-art algorithms for verifying quantum machine learning models.

Robustness Verification of Quantum Machine Learning

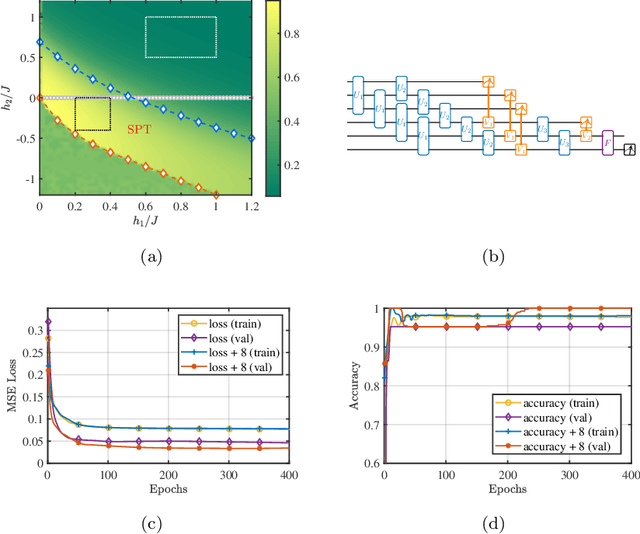
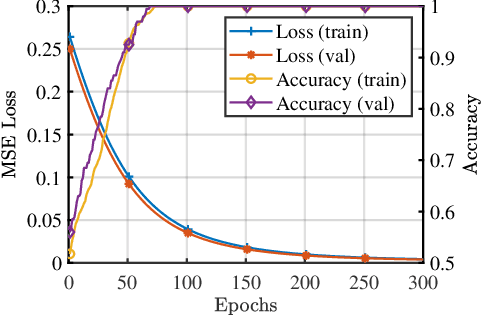
Several important models of machine learning algorithms have been successfully generalized to the quantum world, with potential applications to data analytics in quantum physics that can be implemented on the near future quantum computers. However, noise and decoherence are two major obstacles to the practical implementation of quantum machine learning. In this work, we introduce a general framework for the robustness analysis of quantum machine learning algorithms against noise and decoherence. We argue that fidelity is the only pick of measuring the robustness. A robust bound is derived and an algorithm is developed to check whether or not a quantum machine learning algorithm is robust with respect to the training data. In particular, this algorithm can help to defense attacks and improve the accuracy as it can identify useful new training data during checking. The effectiveness of our robust bound and algorithm is confirmed by the case study of quantum phase recognition. Furthermore, this experiment demonstrates a trade-off between the accuracy of quantum machine learning algorithms and their robustness.