Soft constraint abstraction based on semiring homomorphism
Paper and Code
May 05, 2007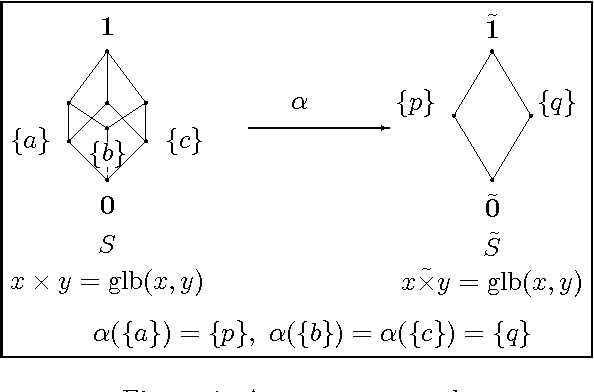
The semiring-based constraint satisfaction problems (semiring CSPs), proposed by Bistarelli, Montanari and Rossi \cite{BMR97}, is a very general framework of soft constraints. In this paper we propose an abstraction scheme for soft constraints that uses semiring homomorphism. To find optimal solutions of the concrete problem, the idea is, first working in the abstract problem and finding its optimal solutions, then using them to solve the concrete problem. In particular, we show that a mapping preserves optimal solutions if and only if it is an order-reflecting semiring homomorphism. Moreover, for a semiring homomorphism $\alpha$ and a problem $P$ over $S$, if $t$ is optimal in $\alpha(P)$, then there is an optimal solution $\bar{t}$ of $P$ such that $\bar{t}$ has the same value as $t$ in $\alpha(P)$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge