Towards Efficient Ansatz Architecture for Variational Quantum Algorithms

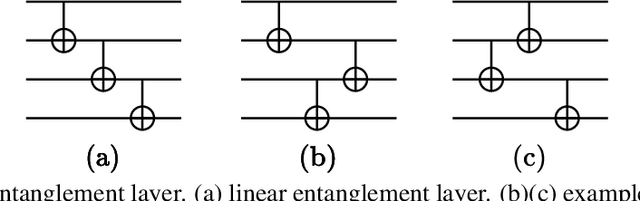
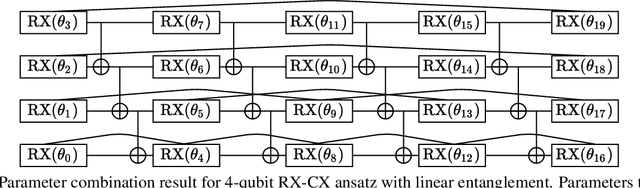
Variational quantum algorithms are expected to demonstrate the advantage of quantum computing on near-term noisy quantum computers. However, training such variational quantum algorithms suffers from gradient vanishing as the size of the algorithm increases. Previous work cannot handle the gradient vanishing induced by the inevitable noise effects on realistic quantum hardware. In this paper, we propose a novel training scheme to mitigate such noise-induced gradient vanishing. We first introduce a new cost function of which the gradients are significantly augmented by employing traceless observables in truncated subspace. We then prove that the same minimum can be reached by optimizing the original cost function with the gradients from the new cost function. Experiments show that our new training scheme is highly effective for major variational quantum algorithms of various tasks.

Mitigating Noise-Induced Gradient Vanishing in Variational Quantum Algorithm Training

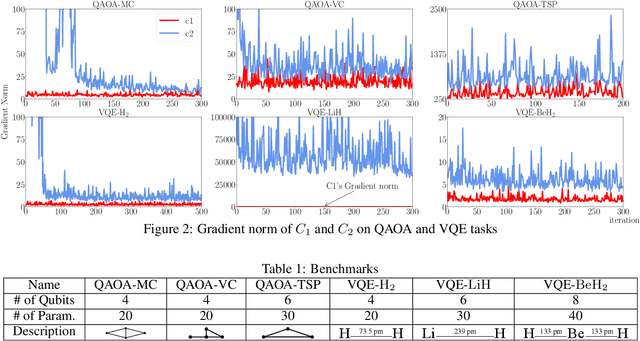
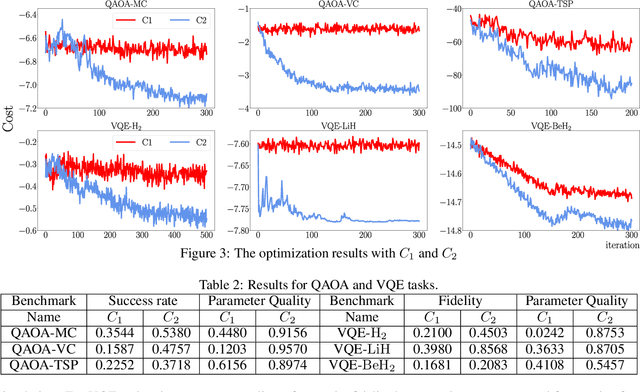
Variational quantum algorithms are expected to demonstrate the advantage of quantum computing on near-term noisy quantum computers. However, training such variational quantum algorithms suffers from gradient vanishing as the size of the algorithm increases. Previous work cannot handle the gradient vanishing induced by the inevitable noise effects on realistic quantum hardware. In this paper, we propose a novel training scheme to mitigate such noise-induced gradient vanishing. We first introduce a new cost function of which the gradients are significantly augmented by employing traceless observables in truncated subspace. We then prove that the same minimum can be reached by optimizing the original cost function with the gradients from the new cost function. Experiments show that our new training scheme is highly effective for major variational quantum algorithms of various tasks.

Poq: Projection-based Runtime Assertions for Debugging on a Quantum Computer

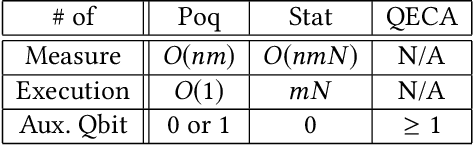
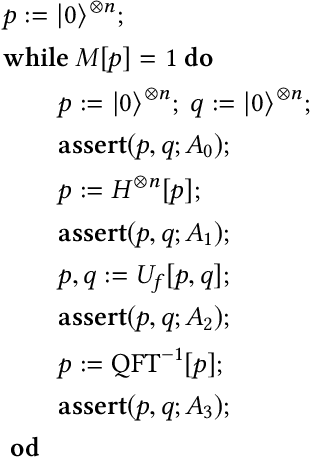
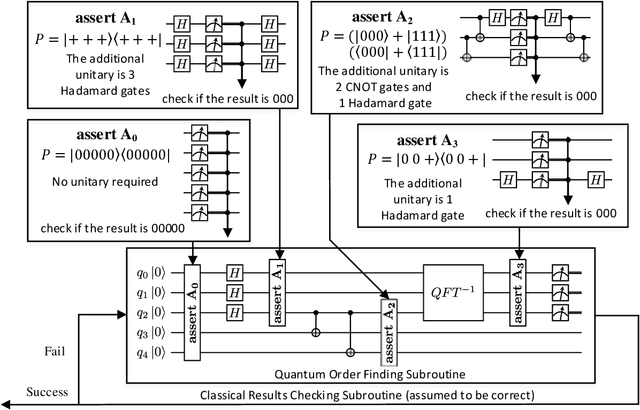
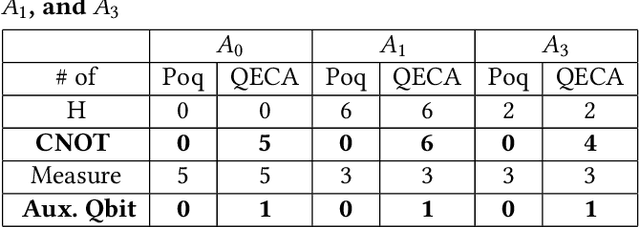
In this paper, we propose Poq, a runtime assertion scheme for debugging on a quantum computer. The predicates in the assertions are represented by projections (or equivalently, closed subspaces of the state space), following Birkhoff-von Neumann quantum logic. The satisfaction of a projection by a quantum state can be directly checked upon a small number of projective measurements rather than a large number of repeated executions. Several techniques are introduced to rotate the predicates to the computational basis, on which a realistic quantum computer usually supports its measurements, so that a satisfying tested state will not be destroyed when an assertion is checked and multi-assertion per testing execution is enabled. We compare Poq with existing quantum program assertions and demonstrate the effectiveness and efficiency of Poq by its applications to assert two sophisticated quantum algorithms.