Towards Efficient Ansatz Architecture for Variational Quantum Algorithms

Variational quantum algorithms are expected to demonstrate the advantage of quantum computing on near-term noisy quantum computers. However, training such variational quantum algorithms suffers from gradient vanishing as the size of the algorithm increases. Previous work cannot handle the gradient vanishing induced by the inevitable noise effects on realistic quantum hardware. In this paper, we propose a novel training scheme to mitigate such noise-induced gradient vanishing. We first introduce a new cost function of which the gradients are significantly augmented by employing traceless observables in truncated subspace. We then prove that the same minimum can be reached by optimizing the original cost function with the gradients from the new cost function. Experiments show that our new training scheme is highly effective for major variational quantum algorithms of various tasks.

Mitigating Noise-Induced Gradient Vanishing in Variational Quantum Algorithm Training

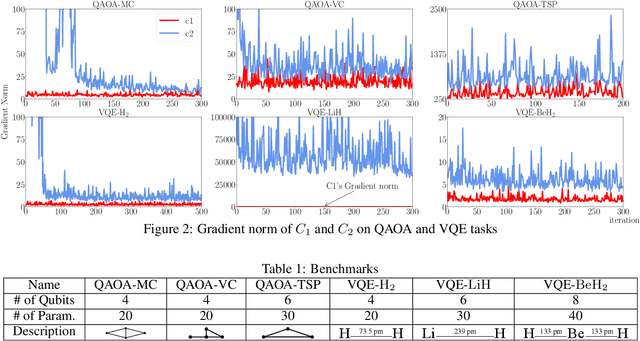
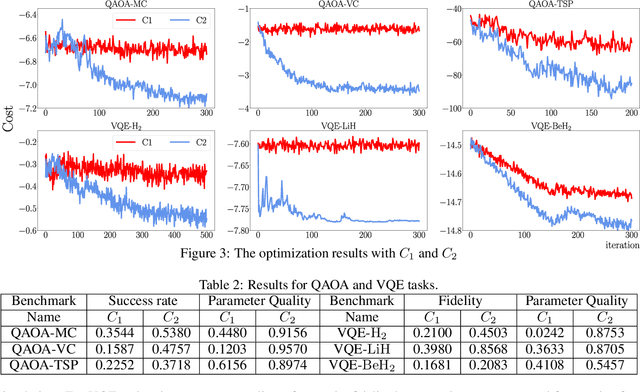
Variational quantum algorithms are expected to demonstrate the advantage of quantum computing on near-term noisy quantum computers. However, training such variational quantum algorithms suffers from gradient vanishing as the size of the algorithm increases. Previous work cannot handle the gradient vanishing induced by the inevitable noise effects on realistic quantum hardware. In this paper, we propose a novel training scheme to mitigate such noise-induced gradient vanishing. We first introduce a new cost function of which the gradients are significantly augmented by employing traceless observables in truncated subspace. We then prove that the same minimum can be reached by optimizing the original cost function with the gradients from the new cost function. Experiments show that our new training scheme is highly effective for major variational quantum algorithms of various tasks.

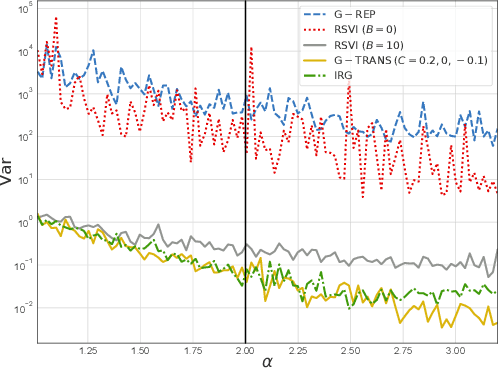
Generalized Transformation-based Gradient

The reparameterization trick has become one of the most useful tools in the field of variational inference. However, the reparameterization trick is based on the standardization transformation which restricts the scope of application of this method to distributions that have tractable inverse cumulative distribution functions or are expressible as deterministic transformations of such distributions. In this paper, we generalized the reparameterization trick by allowing a general transformation. We discover that the proposed model is a special case of control variate indicating that the proposed model can combine the advantages of CV and generalized reparameterization. Based on the proposed gradient model, we propose a new polynomial-based gradient estimator which has better theoretical performance than the reparameterization trick under certain condition and can be applied to a larger class of variational distributions. In studies of synthetic and real data, we show that our proposed gradient estimator has a significantly lower gradient variance than other state-of-the-art methods thus enabling a faster inference procedure.