Generalized Transformation-based Gradient

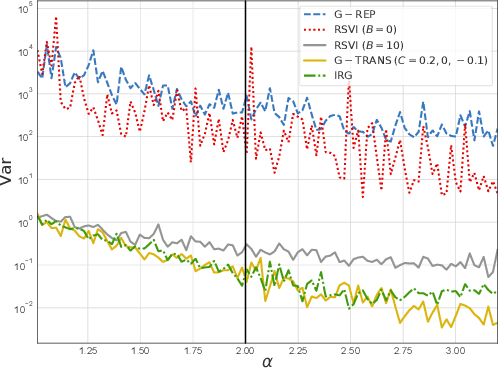
The reparameterization trick has become one of the most useful tools in the field of variational inference. However, the reparameterization trick is based on the standardization transformation which restricts the scope of application of this method to distributions that have tractable inverse cumulative distribution functions or are expressible as deterministic transformations of such distributions. In this paper, we generalized the reparameterization trick by allowing a general transformation. We discover that the proposed model is a special case of control variate indicating that the proposed model can combine the advantages of CV and generalized reparameterization. Based on the proposed gradient model, we propose a new polynomial-based gradient estimator which has better theoretical performance than the reparameterization trick under certain condition and can be applied to a larger class of variational distributions. In studies of synthetic and real data, we show that our proposed gradient estimator has a significantly lower gradient variance than other state-of-the-art methods thus enabling a faster inference procedure.