SmoothVLA: Aligning Vision-Language-Action Models with Physical Constraints via Intrinsic Smoothness Optimization

Vision-Language-Action (VLA) models have emerged as a powerful paradigm for robotic manipulation. However, existing post-training methods face a dilemma between stability and exploration: Supervised Fine-Tuning (SFT) is constrained by demonstration quality and lacks generalization, whereas Reinforcement Learning (RL) improves exploration but often induces erratic, jittery trajectories that violate physical constraints. To bridge this gap, we propose SmoothVLA, a novel reinforcement learning fine-tuning framework that synergistically optimizes task performance and motion smoothness. The technical core is a physics-informed hybrid reward function that integrates binary sparse task rewards with a continuous dense term derived from trajectory jerk. Crucially, this reward is intrinsic, that computing directly from policy rollouts, without requiring extrinsic environment feedback or laborious reward engineering. Leveraging the Group Relative Policy Optimization (GRPO), SmoothVLA establishes trajectory smoothness as an explicit optimization prior, guiding the model toward physically feasible and stable control. Extensive experiments on the LIBERO benchmark demonstrate that SmoothVLA outperforms standard RL by 13.8\% in smoothness and significantly surpasses SFT in generalization across diverse tasks. Our work offers a scalable approach to aligning VLA models with physical-world constraints through intrinsic reward optimization.

Fairness Begins with State: Purifying Latent Preferences for Hierarchical Reinforcement Learning in Interactive Recommendation

Interactive recommender systems (IRS) are increasingly optimized with Reinforcement Learning (RL) to capture the sequential nature of user-system dynamics. However, existing fairness-aware methods often suffer from a fundamental oversight: they assume the observed user state is a faithful representation of true preferences. In reality, implicit feedback is contaminated by popularity-driven noise and exposure bias, creating a distorted state that misleads the RL agent. We argue that the persistent conflict between accuracy and fairness is not merely a reward-shaping issue, but a state estimation failure. In this work, we propose \textbf{DSRM-HRL}, a framework that reformulates fairness-aware recommendation as a latent state purification problem followed by decoupled hierarchical decision-making. We introduce a Denoising State Representation Module (DSRM) based on diffusion models to recover the low-entropy latent preference manifold from high-entropy, noisy interaction histories. Built upon this purified state, a Hierarchical Reinforcement Learning (HRL) agent is employed to decouple conflicting objectives: a high-level policy regulates long-term fairness trajectories, while a low-level policy optimizes short-term engagement under these dynamic constraints. Extensive experiments on high-fidelity simulators (KuaiRec, KuaiRand) demonstrate that DSRM-HRL effectively breaks the "rich-get-richer" feedback loop, achieving a superior Pareto frontier between recommendation utility and exposure equity.

Proactive Guiding Strategy for Item-side Fairness in Interactive Recommendation

Item-side fairness is crucial for ensuring the fair exposure of long-tail items in interactive recommender systems. Existing approaches promote the exposure of long-tail items by directly incorporating them into recommended results. This causes misalignment between user preferences and the recommended long-tail items, which hinders long-term user engagement and reduces the effectiveness of recommendations. We aim for a proactive fairness-guiding strategy, which actively guides user preferences toward long-tail items while preserving user satisfaction during the interactive recommendation process. To this end, we propose HRL4PFG, an interactive recommendation framework that leverages hierarchical reinforcement learning to guide user preferences toward long-tail items progressively. HRL4PFG operates through a macro-level process that generates fairness-guided targets based on multi-step feedback, and a micro-level process that fine-tunes recommendations in real time according to both these targets and evolving user preferences. Extensive experiments show that HRL4PFG improves cumulative interaction rewards and maximum user interaction length by a larger margin when compared with state-of-the-art methods in interactive recommendation environments.

Semantic-guided Representation Learning for Multi-Label Recognition

Multi-label Recognition (MLR) involves assigning multiple labels to each data instance in an image, offering advantages over single-label classification in complex scenarios. However, it faces the challenge of annotating all relevant categories, often leading to uncertain annotations, such as unseen or incomplete labels. Recent Vision and Language Pre-training (VLP) based methods have made significant progress in tackling zero-shot MLR tasks by leveraging rich vision-language correlations. However, the correlation between multi-label semantics has not been fully explored, and the learned visual features often lack essential semantic information. To overcome these limitations, we introduce a Semantic-guided Representation Learning approach (SigRL) that enables the model to learn effective visual and textual representations, thereby improving the downstream alignment of visual images and categories. Specifically, we first introduce a graph-based multi-label correlation module (GMC) to facilitate information exchange between labels, enriching the semantic representation across the multi-label texts. Next, we propose a Semantic Visual Feature Reconstruction module (SVFR) to enhance the semantic information in the visual representation by integrating the learned textual representation during reconstruction. Finally, we optimize the image-text matching capability of the VLP model using both local and global features to achieve zero-shot MLR. Comprehensive experiments are conducted on several MLR benchmarks, encompassing both zero-shot MLR (with unseen labels) and single positive multi-label learning (with limited labels), demonstrating the superior performance of our approach compared to state-of-the-art methods. The code is available at https://github.com/MVL-Lab/SigRL.

Temporal-contextual Event Learning for Pedestrian Crossing Intent Prediction

Ensuring the safety of vulnerable road users through accurate prediction of pedestrian crossing intention (PCI) plays a crucial role in the context of autonomous and assisted driving. Analyzing the set of observation video frames in ego-view has been widely used in most PCI prediction methods to forecast the cross intent. However, they struggle to capture the critical events related to pedestrian behaviour along the temporal dimension due to the high redundancy of the video frames, which results in the sub-optimal performance of PCI prediction. Our research addresses the challenge by introducing a novel approach called \underline{T}emporal-\underline{c}ontextual Event \underline{L}earning (TCL). The TCL is composed of the Temporal Merging Module (TMM), which aims to manage the redundancy by clustering the observed video frames into multiple key temporal events. Then, the Contextual Attention Block (CAB) is employed to adaptively aggregate multiple event features along with visual and non-visual data. By synthesizing the temporal feature extraction and contextual attention on the key information across the critical events, TCL can learn expressive representation for the PCI prediction. Extensive experiments are carried out on three widely adopted datasets, including PIE, JAAD-beh, and JAAD-all. The results show that TCL substantially surpasses the state-of-the-art methods. Our code can be accessed at https://github.com/dadaguailhb/TCL.

IFIR: A Comprehensive Benchmark for Evaluating Instruction-Following in Expert-Domain Information Retrieval

We introduce IFIR, the first comprehensive benchmark designed to evaluate instruction-following information retrieval (IR) in expert domains. IFIR includes 2,426 high-quality examples and covers eight subsets across four specialized domains: finance, law, healthcare, and science literature. Each subset addresses one or more domain-specific retrieval tasks, replicating real-world scenarios where customized instructions are critical. IFIR enables a detailed analysis of instruction-following retrieval capabilities by incorporating instructions at different levels of complexity. We also propose a novel LLM-based evaluation method to provide a more precise and reliable assessment of model performance in following instructions. Through extensive experiments on 15 frontier retrieval models, including those based on LLMs, our results reveal that current models face significant challenges in effectively following complex, domain-specific instructions. We further provide in-depth analyses to highlight these limitations, offering valuable insights to guide future advancements in retriever development.

Self-Supervised Spatial-Temporal Normality Learning for Time Series Anomaly Detection

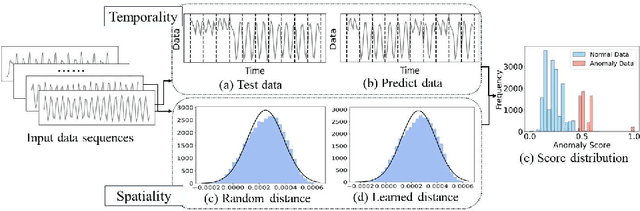
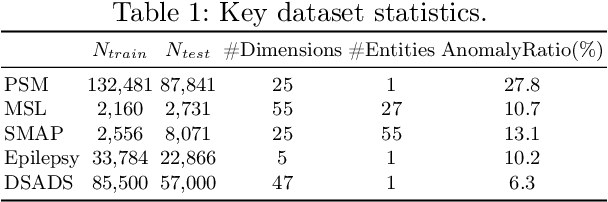
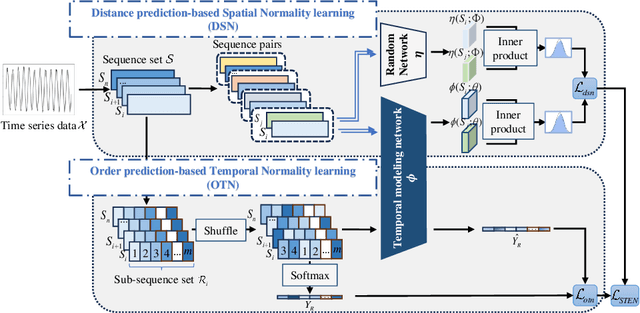
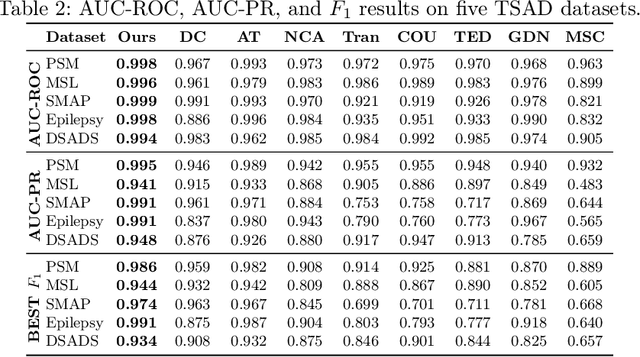
Time Series Anomaly Detection (TSAD) finds widespread applications across various domains such as financial markets, industrial production, and healthcare. Its primary objective is to learn the normal patterns of time series data, thereby identifying deviations in test samples. Most existing TSAD methods focus on modeling data from the temporal dimension, while ignoring the semantic information in the spatial dimension. To address this issue, we introduce a novel approach, called Spatial-Temporal Normality learning (STEN). STEN is composed of a sequence Order prediction-based Temporal Normality learning (OTN) module that captures the temporal correlations within sequences, and a Distance prediction-based Spatial Normality learning (DSN) module that learns the relative spatial relations between sequences in a feature space. By synthesizing these two modules, STEN learns expressive spatial-temporal representations for the normal patterns hidden in the time series data. Extensive experiments on five popular TSAD benchmarks show that STEN substantially outperforms state-of-the-art competing methods. Our code is available at https://github.com/mala-lab/STEN.

Zero Stability Well Predicts Performance of Convolutional Neural Networks

The question of what kind of convolutional neural network (CNN) structure performs well is fascinating. In this work, we move toward the answer with one more step by connecting zero stability and model performance. Specifically, we found that if a discrete solver of an ordinary differential equation is zero stable, the CNN corresponding to that solver performs well. We first give the interpretation of zero stability in the context of deep learning and then investigate the performance of existing first- and second-order CNNs under different zero-stable circumstances. Based on the preliminary observation, we provide a higher-order discretization to construct CNNs and then propose a zero-stable network (ZeroSNet). To guarantee zero stability of the ZeroSNet, we first deduce a structure that meets consistency conditions and then give a zero stable region of a training-free parameter. By analyzing the roots of a characteristic equation, we theoretically obtain the optimal coefficients of feature maps. Empirically, we present our results from three aspects: We provide extensive empirical evidence of different depth on different datasets to show that the moduli of the characteristic equation's roots are the keys for the performance of CNNs that require historical features; Our experiments show that ZeroSNet outperforms existing CNNs which is based on high-order discretization; ZeroSNets show better robustness against noises on the input. The source code is available at \url{https://github.com/LongJin-lab/ZeroSNet}.

Activated Gradients for Deep Neural Networks

Deep neural networks often suffer from poor performance or even training failure due to the ill-conditioned problem, the vanishing/exploding gradient problem, and the saddle point problem. In this paper, a novel method by acting the gradient activation function (GAF) on the gradient is proposed to handle these challenges. Intuitively, the GAF enlarges the tiny gradients and restricts the large gradient. Theoretically, this paper gives conditions that the GAF needs to meet, and on this basis, proves that the GAF alleviates the problems mentioned above. In addition, this paper proves that the convergence rate of SGD with the GAF is faster than that without the GAF under some assumptions. Furthermore, experiments on CIFAR, ImageNet, and PASCAL visual object classes confirm the GAF's effectiveness. The experimental results also demonstrate that the proposed method is able to be adopted in various deep neural networks to improve their performance. The source code is publicly available at https://github.com/LongJin-lab/Activated-Gradients-for-Deep-Neural-Networks.

TempNodeEmb:Temporal Node Embedding considering temporal edge influence matrix

Understanding the evolutionary patterns of real-world evolving complex systems such as human interactions, transport networks, biological interactions, and computer networks has important implications in our daily lives. Predicting future links among the nodes in such networks reveals an important aspect of the evolution of temporal networks. To analyse networks, they are mapped to adjacency matrices, however, a single adjacency matrix cannot represent complex relationships (e.g. temporal pattern), and therefore, some approaches consider a simplified representation of temporal networks but in high-dimensional and generally sparse matrices. As a result, adjacency matrices cannot be directly used by machine learning models for making network or node level predictions. To overcome this problem, automated frameworks are proposed for learning low-dimensional vectors for nodes or edges, as state-of-the-art techniques in predicting temporal patterns in networks such as link prediction. However, these models fail to consider temporal dimensions of the networks. This gap motivated us to propose in this research a new node embedding technique which exploits the evolving nature of the networks considering a simple three-layer graph neural network at each time step, and extracting node orientation by Given's angle method. To prove our proposed algorithm's efficiency, we evaluated the efficiency of our proposed algorithm against six state-of-the-art benchmark network embedding models, on four real temporal networks data, and the results show our model outperforms other methods in predicting future links in temporal networks.