Quality over Quantity: Boosting Data Efficiency Through Ensembled Multimodal Data Curation

In an era overwhelmed by vast amounts of data, the effective curation of web-crawl datasets is essential for optimizing model performance. This paper tackles the challenges associated with the unstructured and heterogeneous nature of such datasets. Traditional heuristic curation methods often inadequately capture complex features, resulting in biases and the exclusion of relevant data. We introduce an advanced, learning-driven approach, Ensemble Curation Of DAta ThroUgh Multimodal Operators (EcoDatum), incorporating a novel quality-guided deduplication method to ensure balanced feature distributions. EcoDatum strategically integrates various unimodal and multimodal data curation operators within a weak supervision ensemble framework, utilizing automated optimization to score each data point effectively. EcoDatum, which significantly improves the data curation quality and efficiency, outperforms existing state-of-the-art (SOTA) techniques, ranked 1st on the DataComp leaderboard, with an average performance score of 0.182 across 38 diverse evaluation datasets. This represents a 28% improvement over the DataComp baseline method, demonstrating its effectiveness in improving dataset curation and model training efficiency.

Key frames assisted hybrid encoding for photorealistic compressive video sensing

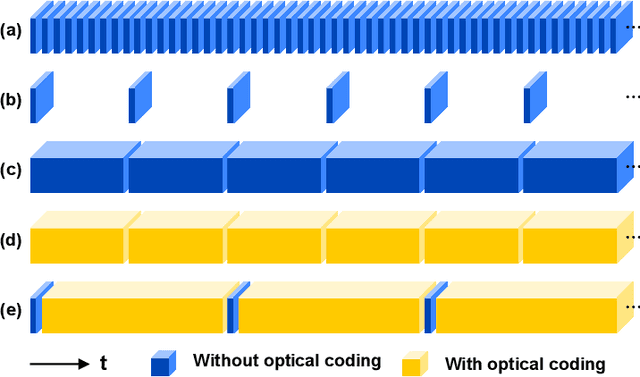
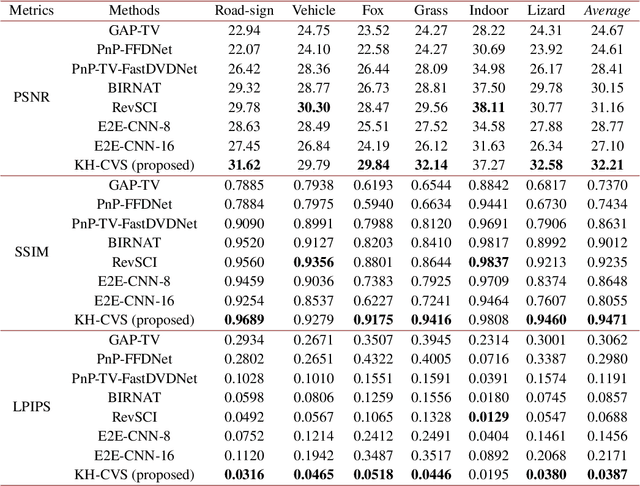
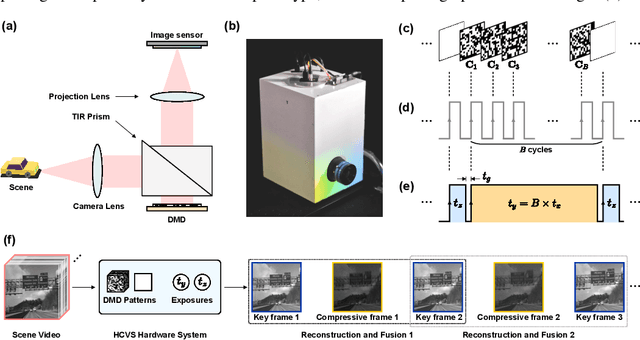
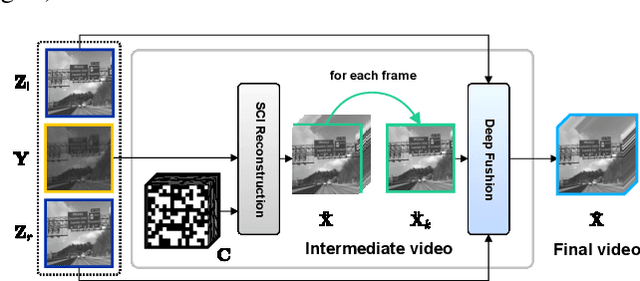
Snapshot compressive imaging (SCI) encodes high-speed scene video into a snapshot measurement and then computationally makes reconstructions, allowing for efficient high-dimensional data acquisition. Numerous algorithms, ranging from regularization-based optimization and deep learning, are being investigated to improve reconstruction quality, but they are still limited by the ill-posed and information-deficient nature of the standard SCI paradigm. To overcome these drawbacks, we propose a new key frames assisted hybrid encoding paradigm for compressive video sensing, termed KH-CVS, that alternatively captures short-exposure key frames without coding and long-exposure encoded compressive frames to jointly reconstruct photorealistic video. With the use of optical flow and spatial warping, a deep convolutional neural network framework is constructed to integrate the benefits of these two types of frames. Extensive experiments on both simulations and real data from the prototype we developed verify the superiority of the proposed method.

DeepOPF-AL: Augmented Learning for Solving AC-OPF Problems with Multiple Load-Solution Mappings

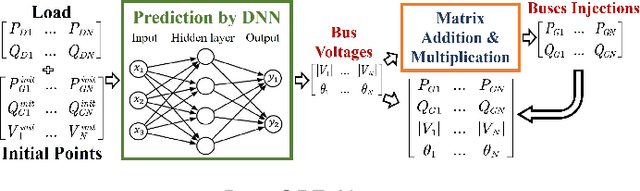
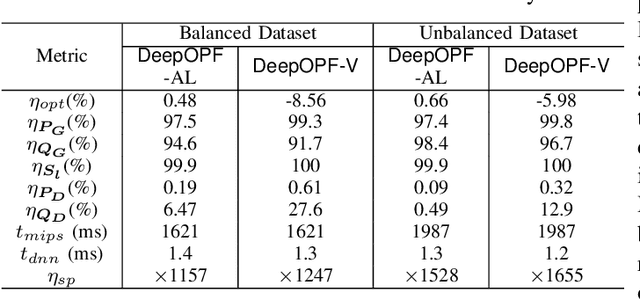
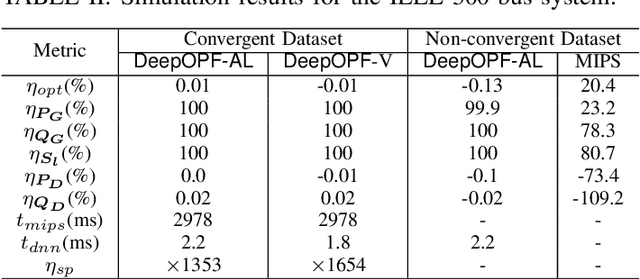
The existence of multiple load-solution mappings of non-convex AC-OPF problems poses a fundamental challenge to deep neural network (DNN) schemes. As the training dataset may contain a mixture of data points corresponding to different load-solution mappings, the DNN can fail to learn a legitimate mapping and generate inferior solutions. We propose DeepOPF-AL as an augmented-learning approach to tackle this issue. The idea is to train a DNN to learn a unique mapping from an augmented input, i.e., (load, initial point), to the solution generated by an iterative OPF solver with the load and initial point as intake. We then apply the learned augmented mapping to solve AC-OPF problems much faster than conventional solvers. Simulation results over IEEE test cases show that DeepOPF-AL achieves noticeably better optimality and similar feasibility and speedup performance, as compared to a recent DNN scheme, with the same DNN size yet elevated training complexity.

Learning-based AC-OPF Solvers on Realistic Network and Realistic Loads

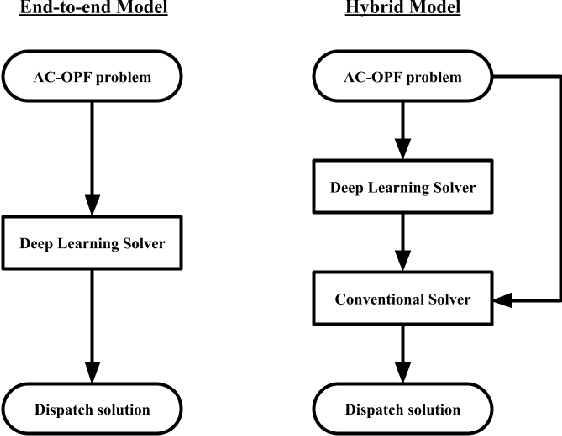
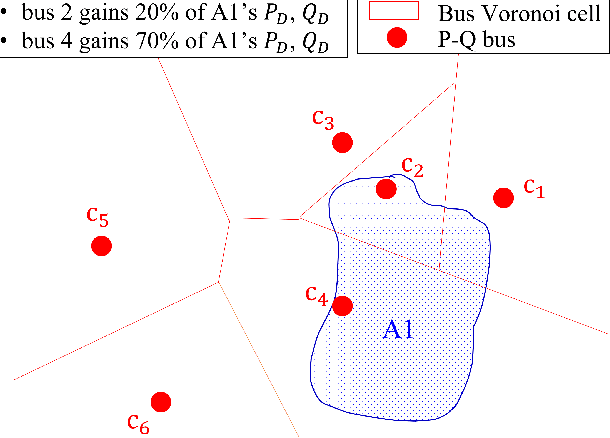
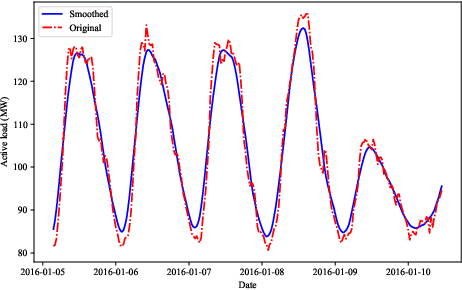
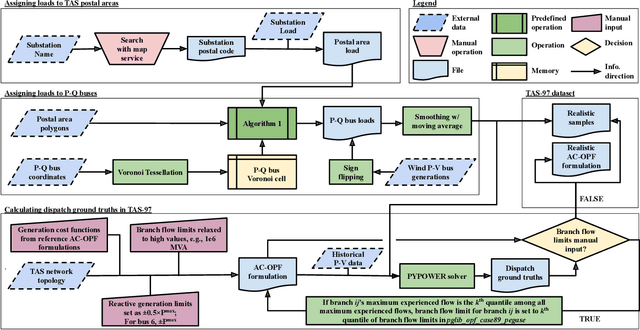
Deep learning approaches for the Alternating Current-Optimal Power Flow (AC-OPF) problem are under active research in recent years. A common shortcoming in this area of research is the lack of a dataset that includes both a realistic power network topology and the corresponding realistic loads. To address this issue, we construct an AC-OPF formulation-ready dataset called TAS-97 that contains realistic network information and realistic bus loads from Tasmania's electricity network. We found that the realistic loads in Tasmania are correlated between buses and they show signs of an underlying multivariate normal distribution. Feasibility-optimized end-to-end deep neural network models are trained and tested on the constructed dataset. Trained on samples with bus loads generated from a fitted multivariate normal distribution, our learning-based AC-OPF solver achieves 0.13% cost optimality gap, 99.73% feasibility rate, and 38.62 times of speedup on realistic testing samples when compared to PYPOWER.

A density peaks clustering algorithm with sparse search and K-d tree

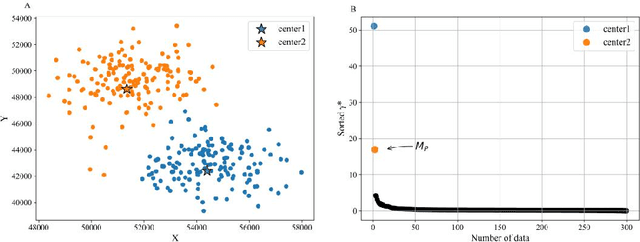
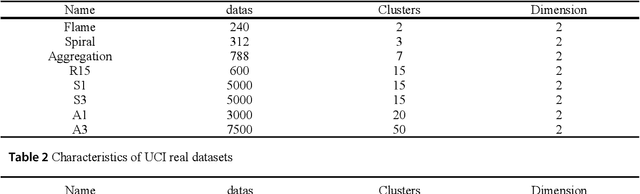
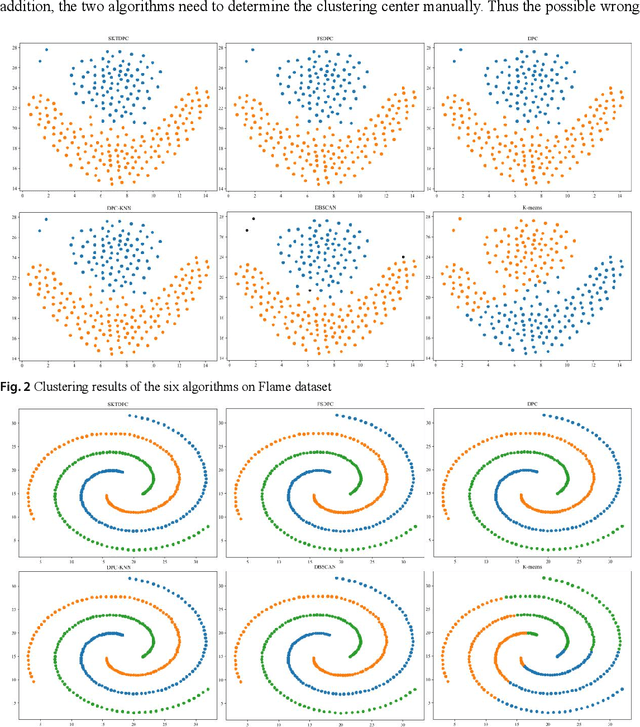
Density peaks clustering has become a nova of clustering algorithm because of its simplicity and practicality. However, there is one main drawback: it is time-consuming due to its high computational complexity. Herein, a density peaks clustering algorithm with sparse search and K-d tree is developed to solve this problem. Firstly, a sparse distance matrix is calculated by using K-d tree to replace the original full rank distance matrix, so as to accelerate the calculation of local density. Secondly, a sparse search strategy is proposed to accelerate the computation of relative-separation with the intersection between the set of k nearest neighbors and the set consisting of the data points with larger local density for any data point. Furthermore, a second-order difference method for decision values is adopted to determine the cluster centers adaptively. Finally, experiments are carried out on datasets with different distribution characteristics, by comparing with other five typical clustering algorithms. It is proved that the algorithm can effectively reduce the computational complexity. Especially for larger datasets, the efficiency is elevated more remarkably. Moreover, the clustering accuracy is also improved to a certain extent. Therefore, it can be concluded that the overall performance of the newly proposed algorithm is excellent.

Ensuring DNN Solution Feasibility for Optimization Problems with Convex Constraints and Its Application to DC Optimal Power Flow Problems

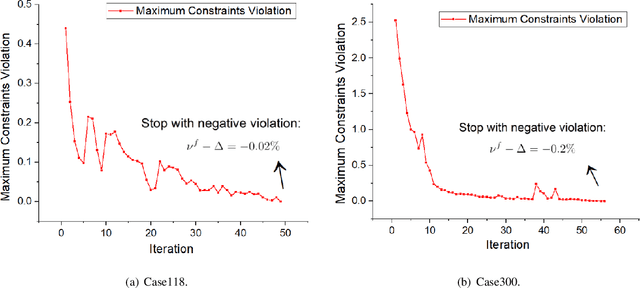
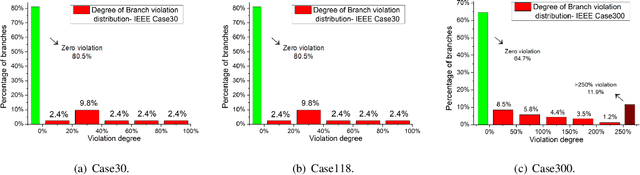
Ensuring solution feasibility is a key challenge in developing Deep Neural Network (DNN) schemes for solving constrained optimization problems, due to inherent DNN prediction errors. In this paper, we propose a "preventive learning'" framework to systematically guarantee DNN solution feasibility for problems with convex constraints and general objective functions. We first apply a predict-and-reconstruct design to not only guarantee equality constraints but also exploit them to reduce the number of variables to be predicted by DNN. Then, as a key methodological contribution, we systematically calibrate inequality constraints used in DNN training, thereby anticipating prediction errors and ensuring the resulting solutions remain feasible. We characterize the calibration magnitudes and the DNN size sufficient for ensuring universal feasibility. We propose a new Adversary-Sample Aware training algorithm to improve DNN's optimality performance without sacrificing feasibility guarantee. Overall, the framework provides two DNNs. The first one from characterizing the sufficient DNN size can guarantee universal feasibility while the other from the proposed training algorithm further improves optimality and maintains DNN's universal feasibility simultaneously. We apply the preventive learning framework to develop DeepOPF+ for solving the essential DC optimal power flow problem in grid operation. It improves over existing DNN-based schemes in ensuring feasibility and attaining consistent desirable speedup performance in both light-load and heavy-load regimes. Simulation results over IEEE Case-30/118/300 test cases show that DeepOPF+ generates $100\%$ feasible solutions with $<$0.5% optimality loss and up to two orders of magnitude computational speedup, as compared to a state-of-the-art iterative solver.

Principle-driven Fiber Transmission Model based on PINN Neural Network

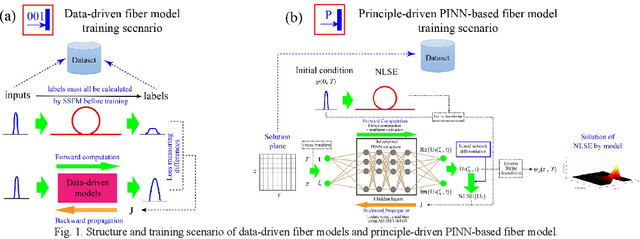
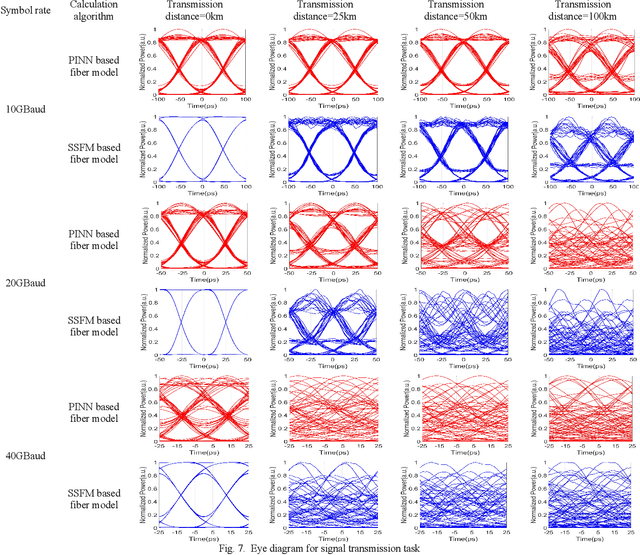
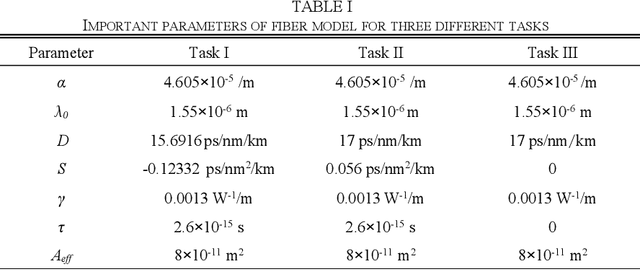
In this paper, a novel principle-driven fiber transmission model based on physical induced neural network (PINN) is proposed. Unlike data-driven models which regard fiber transmission problem as data regression tasks, this model views it as an equation solving problem. Instead of adopting input signals and output signals which are calculated by SSFM algorithm in advance before training, this principle-driven PINN based fiber model adopts frames of time and distance as its inputs and the corresponding real and imaginary parts of NLSE solutions as its outputs. By taking into account of pulses and signals before transmission as initial conditions and fiber physical principles as NLSE in the design of loss functions, this model will progressively learn the transmission rules. Therefore, it can be effectively trained without the data labels, referred as the pre-calculated signals after transmission in data-driven models. Due to this advantage, SSFM algorithm is no longer needed before the training of principle-driven fiber model which can save considerable time consumption. Through numerical demonstration, the results show that this principle-driven PINN based fiber model can handle the prediction tasks of pulse evolution, signal transmission and fiber birefringence for different transmission parameters of fiber telecommunications.

DeepOPF-V: Solving AC-OPF Problems Efficiently

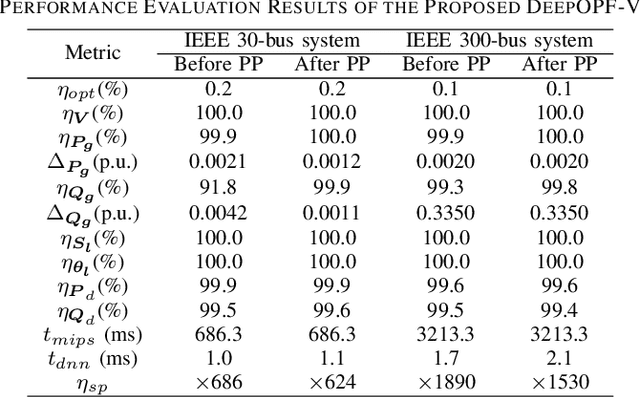
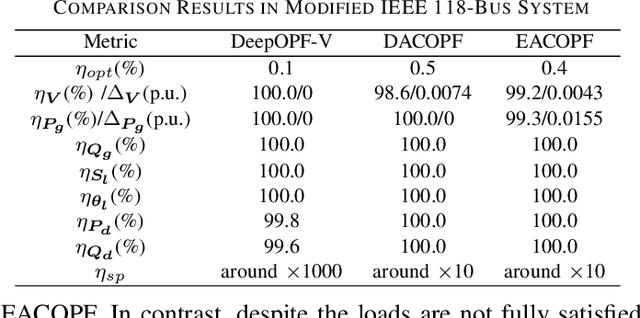
AC optimal power flow (AC-OPF) problems need to be solved more frequently in the future to maintain stable and economic operation. To tackle this challenge, a deep neural network-based voltage-constrained approach (DeepOPF-V) is proposed to find feasible solutions with high computational efficiency. It predicts voltages of all buses and then uses them to obtain all remaining variables. A fast post-processing method is developed to enforce generation constraints. The effectiveness of DeepOPF-V is validated by case studies of several IEEE test systems. Compared with existing approaches, DeepOPF-V achieves a state-of-art computation speedup up to three orders of magnitude and has better performance in preserving the feasibility of the solution.

DeepOPF: A Feasibility-Optimized Deep Neural Network Approach for AC Optimal Power Flow Problems

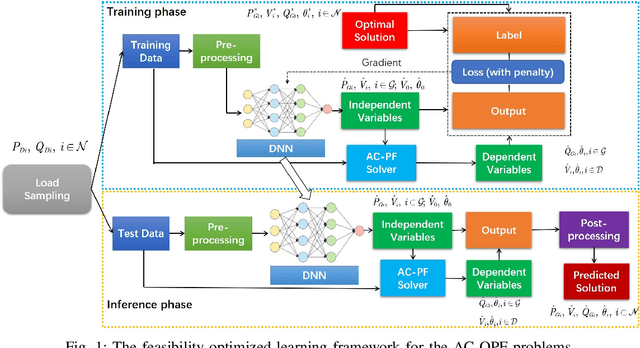
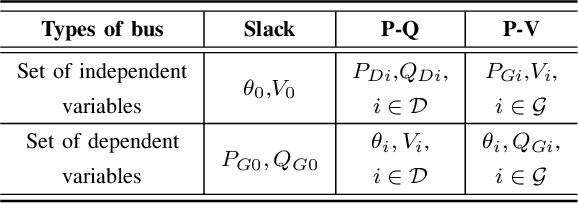
The AC-OPF problem is the key and challenging problem in the power system operation. When solving the AC-OPF problem, the feasibility issue is critical. In this paper, we develop an efficient Deep Neural Network (DNN) approach, DeepOPF, to ensure the feasibility of the generated solution. The idea is to train a DNN model to predict a set of independent operating variables, and then to directly compute the remaining dependable variables by solving the AC power flow equations. While this guarantees the power-flow balances, the principal difficulty lies in ensuring that the obtained solutions satisfy the operation limits of generations, voltages, and branch flow. We tackle this hurdle by employing a penalty approach in training the DNN. As the penalty gradients make the common first-order gradient-based algorithms prohibited due to the hardness of obtaining an explicit-form expression of the penalty gradients, we further apply a zero-order optimization technique to design the training algorithm to address the critical issue. The simulation results of the IEEE test case demonstrate the effectiveness of the penalty approach. Also, they show that DeepOPF can speed up the computing time by one order of magnitude compared to a state-of-the-art solver, at the expense of minor optimality loss.

DeepOPF: A Deep Neural Network Approach for Security-Constrained DC Optimal Power Flow

We develop DeepOPF as a Deep Neural Network (DNN) approach for solving security-constrained direct current optimal power flow (SC-DCOPF) problems, which are critical for reliable and cost-effective power system operation. DeepOPF is inspired by the observation that solving the SC-DCOPF problem for a given power network is equivalent to depicting a high-dimensional mapping between load inputs and generation and phase-angle outputs. We first construct and train a DNN to learn the mapping between the load inputs and the generations. We then directly compute the phase angles from the generations and loads by using the (linearized) power flow equations. Such a two-step procedure significantly reduces the dimension of the mapping to learn, subsequently cutting down the size of the DNN and the amount of training data/time needed. We further characterize a condition that allows us to tune the size of our neural network according to the desired approximation accuracy of the load-to-generation mapping. Simulation results of IEEE test cases show that DeepOPF always generates feasible solutions with negligible optimality loss, while speeding up the computing time by up to 400x as compared to a state-of-the-art solver.