Learning Dynamic Local Context Representations for Infrared Small Target Detection

Infrared small target detection (ISTD) is challenging due to complex backgrounds, low signal-to-clutter ratios, and varying target sizes and shapes. Effective detection relies on capturing local contextual information at the appropriate scale. However, small-kernel CNNs have limited receptive fields, leading to false alarms, while transformer models, with global receptive fields, often treat small targets as noise, resulting in miss-detections. Hybrid models struggle to bridge the semantic gap between CNNs and transformers, causing high complexity.To address these challenges, we propose LCRNet, a novel method that learns dynamic local context representations for ISTD. The model consists of three components: (1) C2FBlock, inspired by PDE solvers, for efficient small target information capture; (2) DLC-Attention, a large-kernel attention mechanism that dynamically builds context and reduces feature redundancy; and (3) HLKConv, a hierarchical convolution operator based on large-kernel decomposition that preserves sparsity and mitigates the drawbacks of dilated convolutions. Despite its simplicity, with only 1.65M parameters, LCRNet achieves state-of-the-art (SOTA) performance.Experiments on multiple datasets, comparing LCRNet with 33 SOTA methods, demonstrate its superior performance and efficiency.

A density peaks clustering algorithm with sparse search and K-d tree

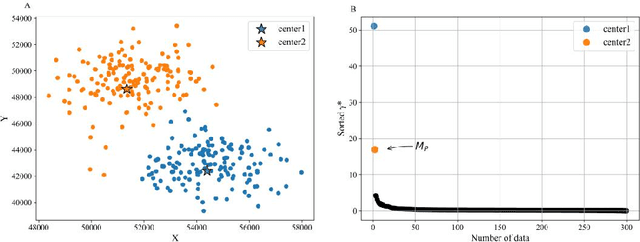
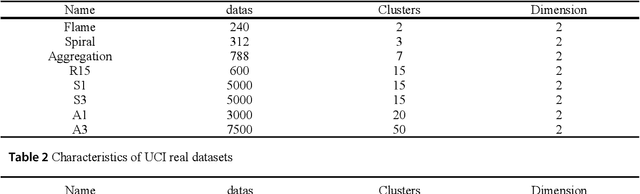
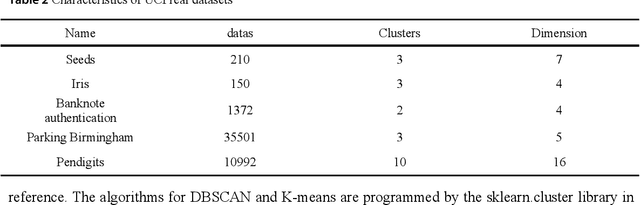
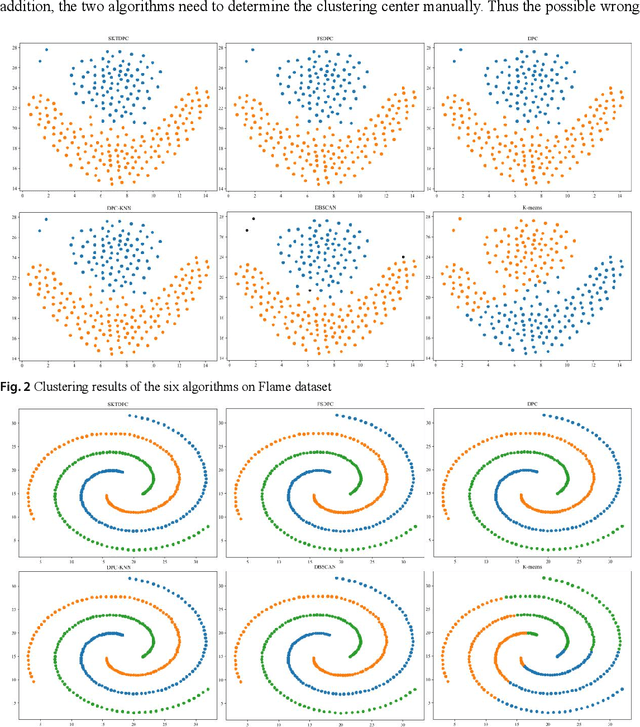
Density peaks clustering has become a nova of clustering algorithm because of its simplicity and practicality. However, there is one main drawback: it is time-consuming due to its high computational complexity. Herein, a density peaks clustering algorithm with sparse search and K-d tree is developed to solve this problem. Firstly, a sparse distance matrix is calculated by using K-d tree to replace the original full rank distance matrix, so as to accelerate the calculation of local density. Secondly, a sparse search strategy is proposed to accelerate the computation of relative-separation with the intersection between the set of k nearest neighbors and the set consisting of the data points with larger local density for any data point. Furthermore, a second-order difference method for decision values is adopted to determine the cluster centers adaptively. Finally, experiments are carried out on datasets with different distribution characteristics, by comparing with other five typical clustering algorithms. It is proved that the algorithm can effectively reduce the computational complexity. Especially for larger datasets, the efficiency is elevated more remarkably. Moreover, the clustering accuracy is also improved to a certain extent. Therefore, it can be concluded that the overall performance of the newly proposed algorithm is excellent.