Steven H. Low
DeepOPF-AL: Augmented Learning for Solving AC-OPF Problems with Multiple Load-Solution Mappings
Jun 07, 2022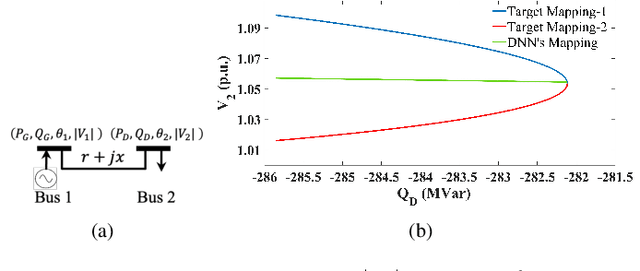
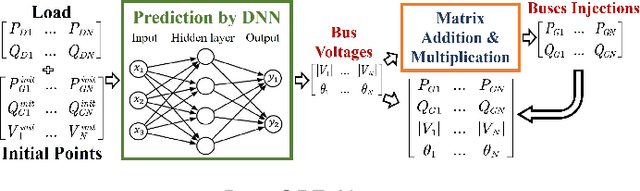
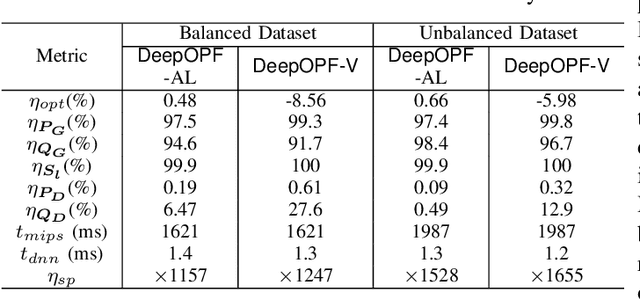
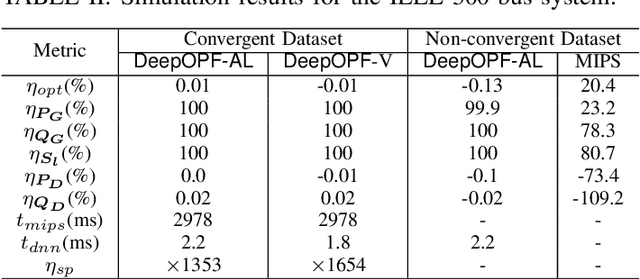
Abstract:The existence of multiple load-solution mappings of non-convex AC-OPF problems poses a fundamental challenge to deep neural network (DNN) schemes. As the training dataset may contain a mixture of data points corresponding to different load-solution mappings, the DNN can fail to learn a legitimate mapping and generate inferior solutions. We propose DeepOPF-AL as an augmented-learning approach to tackle this issue. The idea is to train a DNN to learn a unique mapping from an augmented input, i.e., (load, initial point), to the solution generated by an iterative OPF solver with the load and initial point as intake. We then apply the learned augmented mapping to solve AC-OPF problems much faster than conventional solvers. Simulation results over IEEE test cases show that DeepOPF-AL achieves noticeably better optimality and similar feasibility and speedup performance, as compared to a recent DNN scheme, with the same DNN size yet elevated training complexity.
Ensuring DNN Solution Feasibility for Optimization Problems with Convex Constraints and Its Application to DC Optimal Power Flow Problems
Dec 15, 2021

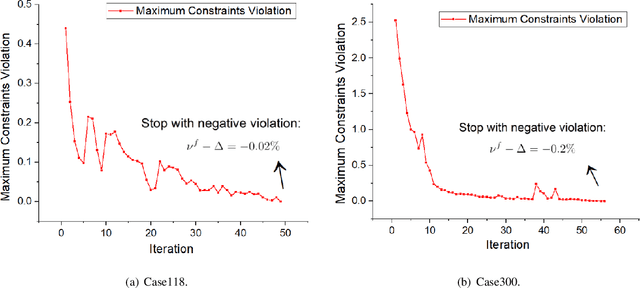
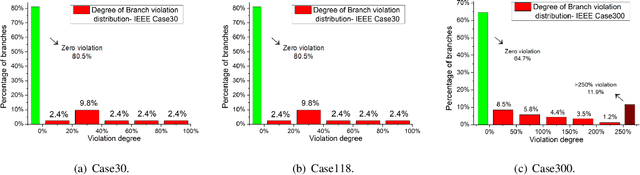
Abstract:Ensuring solution feasibility is a key challenge in developing Deep Neural Network (DNN) schemes for solving constrained optimization problems, due to inherent DNN prediction errors. In this paper, we propose a "preventive learning'" framework to systematically guarantee DNN solution feasibility for problems with convex constraints and general objective functions. We first apply a predict-and-reconstruct design to not only guarantee equality constraints but also exploit them to reduce the number of variables to be predicted by DNN. Then, as a key methodological contribution, we systematically calibrate inequality constraints used in DNN training, thereby anticipating prediction errors and ensuring the resulting solutions remain feasible. We characterize the calibration magnitudes and the DNN size sufficient for ensuring universal feasibility. We propose a new Adversary-Sample Aware training algorithm to improve DNN's optimality performance without sacrificing feasibility guarantee. Overall, the framework provides two DNNs. The first one from characterizing the sufficient DNN size can guarantee universal feasibility while the other from the proposed training algorithm further improves optimality and maintains DNN's universal feasibility simultaneously. We apply the preventive learning framework to develop DeepOPF+ for solving the essential DC optimal power flow problem in grid operation. It improves over existing DNN-based schemes in ensuring feasibility and attaining consistent desirable speedup performance in both light-load and heavy-load regimes. Simulation results over IEEE Case-30/118/300 test cases show that DeepOPF+ generates $100\%$ feasible solutions with $<$0.5% optimality loss and up to two orders of magnitude computational speedup, as compared to a state-of-the-art iterative solver.
DeepOPF-V: Solving AC-OPF Problems Efficiently
Mar 22, 2021
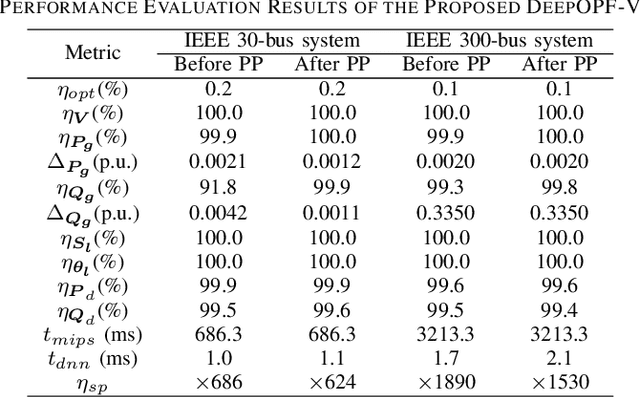
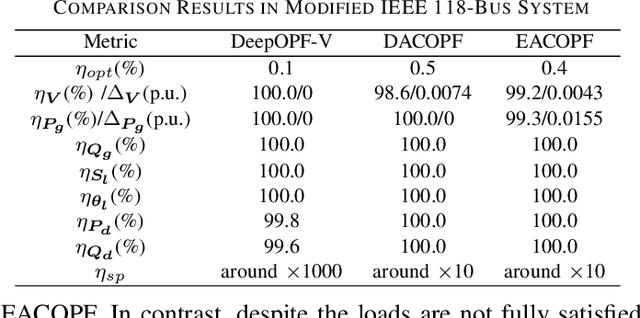
Abstract:AC optimal power flow (AC-OPF) problems need to be solved more frequently in the future to maintain stable and economic operation. To tackle this challenge, a deep neural network-based voltage-constrained approach (DeepOPF-V) is proposed to find feasible solutions with high computational efficiency. It predicts voltages of all buses and then uses them to obtain all remaining variables. A fast post-processing method is developed to enforce generation constraints. The effectiveness of DeepOPF-V is validated by case studies of several IEEE test systems. Compared with existing approaches, DeepOPF-V achieves a state-of-art computation speedup up to three orders of magnitude and has better performance in preserving the feasibility of the solution.
DeepOPF: A Feasibility-Optimized Deep Neural Network Approach for AC Optimal Power Flow Problems
Jul 02, 2020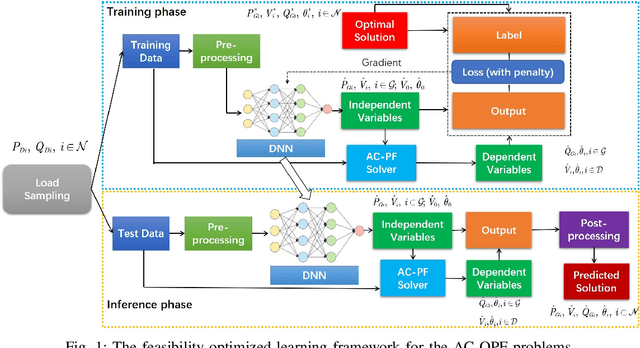
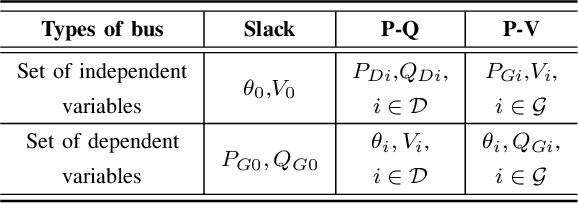

Abstract:The AC-OPF problem is the key and challenging problem in the power system operation. When solving the AC-OPF problem, the feasibility issue is critical. In this paper, we develop an efficient Deep Neural Network (DNN) approach, DeepOPF, to ensure the feasibility of the generated solution. The idea is to train a DNN model to predict a set of independent operating variables, and then to directly compute the remaining dependable variables by solving the AC power flow equations. While this guarantees the power-flow balances, the principal difficulty lies in ensuring that the obtained solutions satisfy the operation limits of generations, voltages, and branch flow. We tackle this hurdle by employing a penalty approach in training the DNN. As the penalty gradients make the common first-order gradient-based algorithms prohibited due to the hardness of obtaining an explicit-form expression of the penalty gradients, we further apply a zero-order optimization technique to design the training algorithm to address the critical issue. The simulation results of the IEEE test case demonstrate the effectiveness of the penalty approach. Also, they show that DeepOPF can speed up the computing time by one order of magnitude compared to a state-of-the-art solver, at the expense of minor optimality loss.
On Identification of Distribution Grids
Nov 05, 2017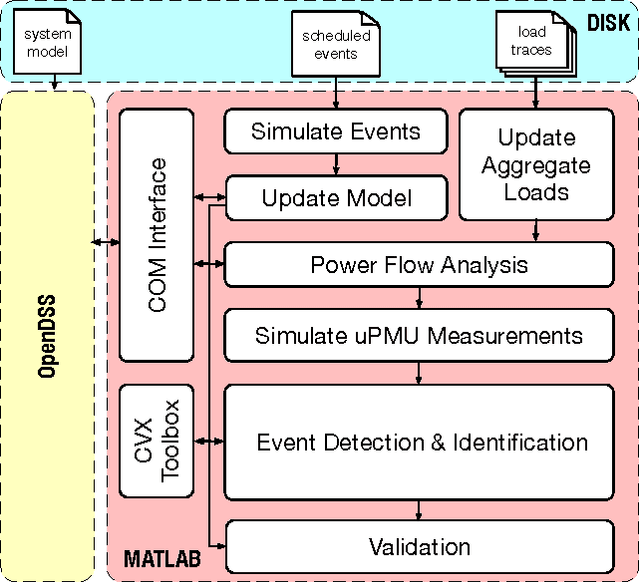
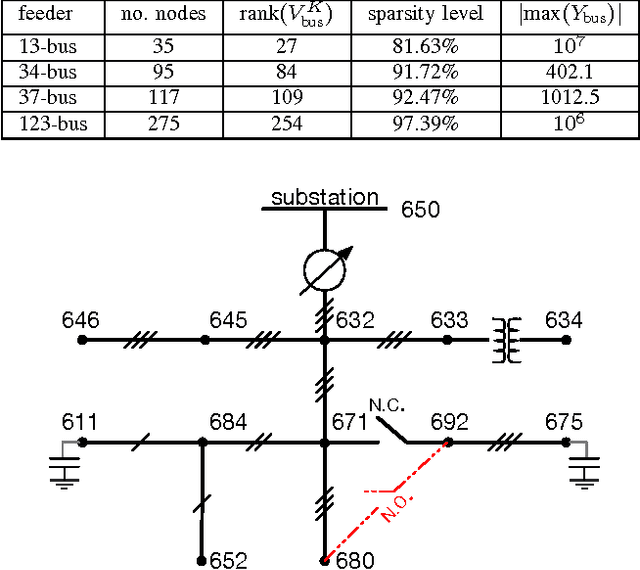
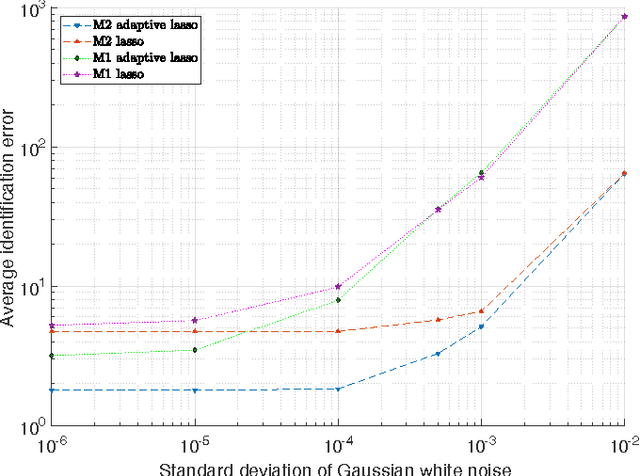
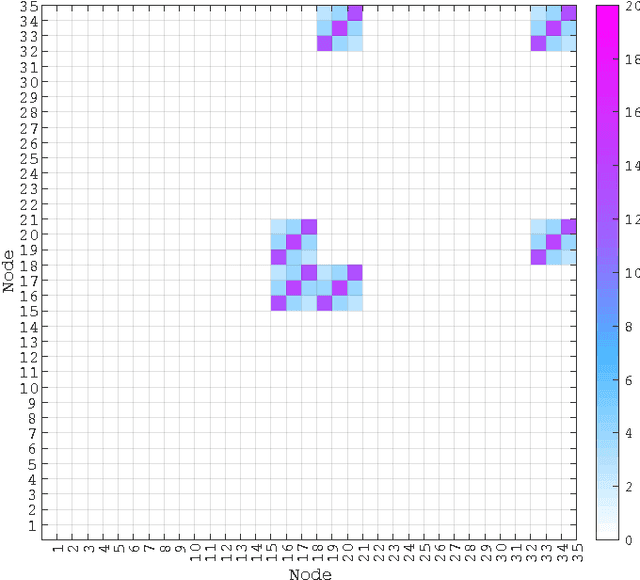
Abstract:Large-scale integration of distributed energy resources into residential distribution feeders necessitates careful control of their operation through power flow analysis. While the knowledge of the distribution system model is crucial for this type of analysis, it is often unavailable or outdated. The recent introduction of synchrophasor technology in low-voltage distribution grids has created an unprecedented opportunity to learn this model from high-precision, time-synchronized measurements of voltage and current phasors at various locations. This paper focuses on joint estimation of model parameters (admittance values) and operational structure of a poly-phase distribution network from the available telemetry data via the lasso, a method for regression shrinkage and selection. We propose tractable convex programs capable of tackling the low rank structure of the distribution system and develop an online algorithm for early detection and localization of critical events that induce a change in the admittance matrix. The efficacy of these techniques is corroborated through power flow studies on four three-phase radial distribution systems serving real household demands.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge