A Communication and Computation Efficient Fully First-order Method for Decentralized Bilevel Optimization

Bilevel optimization, crucial for hyperparameter tuning, meta-learning and reinforcement learning, remains less explored in the decentralized learning paradigm, such as decentralized federated learning (DFL). Typically, decentralized bilevel methods rely on both gradients and Hessian matrices to approximate hypergradients of upper-level models. However, acquiring and sharing the second-order oracle is compute and communication intensive. % and sharing this information incurs heavy communication overhead. To overcome these challenges, this paper introduces a fully first-order decentralized method for decentralized Bilevel optimization, $\text{C}^2$DFB which is both compute- and communicate-efficient. In $\text{C}^2$DFB, each learning node optimizes a min-min-max problem to approximate hypergradient by exclusively using gradients information. To reduce the traffic load at the inner-loop of solving the lower-level problem, $\text{C}^2$DFB incorporates a lightweight communication protocol for efficiently transmitting compressed residuals of local parameters. % during the inner loops. Rigorous theoretical analysis ensures its convergence % of the algorithm, indicating a first-order oracle calls of $\tilde{\mathcal{O}}(\epsilon^{-4})$. Experiments on hyperparameter tuning and hyper-representation tasks validate the superiority of $\text{C}^2$DFB across various typologies and heterogeneous data distributions.

Active Task-Inference-Guided Deep Inverse Reinforcement Learning

In inverse reinforcement learning (IRL), given a Markov decision process (MDP) and a set of demonstrations for completing a task, the objective is to learn a reward function to explain the demonstrations. However, it is challenging to apply IRL in tasks where a proper memory structure is the key to complete the task. To address this challenge, we develop an iterative algorithm that alternates between a task inference module that infers the high-level memory structure of the task and a reward learning module that learns a reward function with the inferred memory structure. In each iteration, the task inference module produces a series of queries to be answered by the demonstrator. Each query asks whether a sequence of high-level events leads to the completion of the task. The demonstrator then provides a demonstration executing the sequence to answer each query. After the queries are answered, the task inference module returns a hypothesis deterministic finite automaton (DFA) encoding the high-level memory structure to be used by the reward learning. The reward learning module incorporates the DFA states into the MDP states and creates a product automaton. Then the reward learning module proceeds to learn a Markovian reward function for this product automaton by performing deep maximum entropy IRL. At the end of each iteration, the algorithm computes an optimal policy with respect to the learned reward. This iterative process continues until the computed policy leads to satisfactory performance in completing the task. The experiments show that the proposed algorithm outperforms three IRL baselines in task performance.

Fairness with Dynamics

It has recently been shown that if feedback effects of decisions are ignored, then imposing fairness constraints such as demographic parity or equality of opportunity can actually exacerbate unfairness. We propose to address this challenge by modeling feedback effects as the dynamics of a Markov decision processes (MDPs). First, we define analogs of fairness properties that have been proposed for supervised learning. Second, we propose algorithms for learning fair decision-making policies for MDPs. We also explore extensions to reinforcement learning, where parts of the dynamical system are unknown and must be learned without violating fairness. Finally, we demonstrate the need to account for dynamical effects using simulations on a loan applicant MDP.

Environment-Independent Task Specifications via GLTL

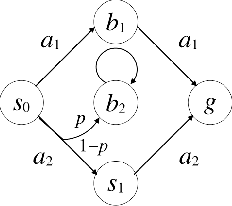
We propose a new task-specification language for Markov decision processes that is designed to be an improvement over reward functions by being environment independent. The language is a variant of Linear Temporal Logic (LTL) that is extended to probabilistic specifications in a way that permits approximations to be learned in finite time. We provide several small environments that demonstrate the advantages of our geometric LTL (GLTL) language and illustrate how it can be used to specify standard reinforcement-learning tasks straightforwardly.

Correct-by-synthesis reinforcement learning with temporal logic constraints

We consider a problem on the synthesis of reactive controllers that optimize some a priori unknown performance criterion while interacting with an uncontrolled environment such that the system satisfies a given temporal logic specification. We decouple the problem into two subproblems. First, we extract a (maximally) permissive strategy for the system, which encodes multiple (possibly all) ways in which the system can react to the adversarial environment and satisfy the specifications. Then, we quantify the a priori unknown performance criterion as a (still unknown) reward function and compute an optimal strategy for the system within the operating envelope allowed by the permissive strategy by using the so-called maximin-Q learning algorithm. We establish both correctness (with respect to the temporal logic specifications) and optimality (with respect to the a priori unknown performance criterion) of this two-step technique for a fragment of temporal logic specifications. For specifications beyond this fragment, correctness can still be preserved, but the learned strategy may be sub-optimal. We present an algorithm to the overall problem, and demonstrate its use and computational requirements on a set of robot motion planning examples.