LLM4ED: Large Language Models for Automatic Equation Discovery

Equation discovery is aimed at directly extracting physical laws from data and has emerged as a pivotal research domain. Previous methods based on symbolic mathematics have achieved substantial advancements, but often require the design of implementation of complex algorithms. In this paper, we introduce a new framework that utilizes natural language-based prompts to guide large language models (LLMs) in automatically mining governing equations from data. Specifically, we first utilize the generation capability of LLMs to generate diverse equations in string form, and then evaluate the generated equations based on observations. In the optimization phase, we propose two alternately iterated strategies to optimize generated equations collaboratively. The first strategy is to take LLMs as a black-box optimizer and achieve equation self-improvement based on historical samples and their performance. The second strategy is to instruct LLMs to perform evolutionary operators for global search. Experiments are extensively conducted on both partial differential equations and ordinary differential equations. Results demonstrate that our framework can discover effective equations to reveal the underlying physical laws under various nonlinear dynamic systems. Further comparisons are made with state-of-the-art models, demonstrating good stability and usability. Our framework substantially lowers the barriers to learning and applying equation discovery techniques, demonstrating the application potential of LLMs in the field of knowledge discovery.

A knowledge-based data-driven framework for all-day identification of cloud types using satellite remote sensing

Cloud types, as a type of meteorological data, are of particular significance for evaluating changes in rainfall, heatwaves, water resources, floods and droughts, food security and vegetation cover, as well as land use. In order to effectively utilize high-resolution geostationary observations, a knowledge-based data-driven (KBDD) framework for all-day identification of cloud types based on spectral information from Himawari-8/9 satellite sensors is designed. And a novel, simple and efficient network, named CldNet, is proposed. Compared with widely used semantic segmentation networks, including SegNet, PSPNet, DeepLabV3+, UNet, and ResUnet, our proposed model CldNet with an accuracy of 80.89+-2.18% is state-of-the-art in identifying cloud types and has increased by 32%, 46%, 22%, 2%, and 39%, respectively. With the assistance of auxiliary information (e.g., satellite zenith/azimuth angle, solar zenith/azimuth angle), the accuracy of CldNet-W using visible and near-infrared bands and CldNet-O not using visible and near-infrared bands on the test dataset is 82.23+-2.14% and 73.21+-2.02%, respectively. Meanwhile, the total parameters of CldNet are only 0.46M, making it easy for edge deployment. More importantly, the trained CldNet without any fine-tuning can predict cloud types with higher spatial resolution using satellite spectral data with spatial resolution 0.02{\deg}*0.02{\deg}, which indicates that CldNet possesses a strong generalization ability. In aggregate, the KBDD framework using CldNet is a highly effective cloud-type identification system capable of providing a high-fidelity, all-day, spatiotemporal cloud-type database for many climate assessment fields.

Physics-constrained robust learning of open-form PDEs from limited and noisy data

Unveiling the underlying governing equations of nonlinear dynamic systems remains a significant challenge, especially when encountering noisy observations and no prior knowledge available. This study proposes R-DISCOVER, a framework designed to robustly uncover open-form partial differential equations (PDEs) from limited and noisy data. The framework operates through two alternating update processes: discovering and embedding. The discovering phase employs symbolic representation and a reinforcement learning (RL)-guided hybrid PDE generator to efficiently produce diverse open-form PDEs with tree structures. A neural network-based predictive model fits the system response and serves as the reward evaluator for the generated PDEs. PDEs with superior fits are utilized to iteratively optimize the generator via the RL method and the best-performing PDE is selected by a parameter-free stability metric. The embedding phase integrates the initially identified PDE from the discovering process as a physical constraint into the predictive model for robust training. The traversal of PDE trees automates the construction of the computational graph and the embedding process without human intervention. Numerical experiments demonstrate our framework's capability to uncover governing equations from nonlinear dynamic systems with limited and highly noisy data and outperform other physics-informed neural network-based discovery methods. This work opens new potential for exploring real-world systems with limited understanding.

DISCOVER: Deep identification of symbolic open-form PDEs via enhanced reinforcement-learning

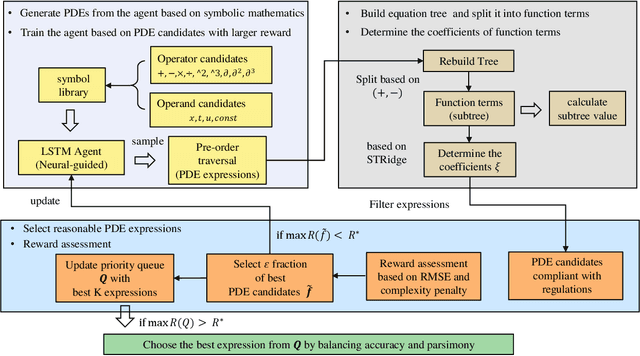
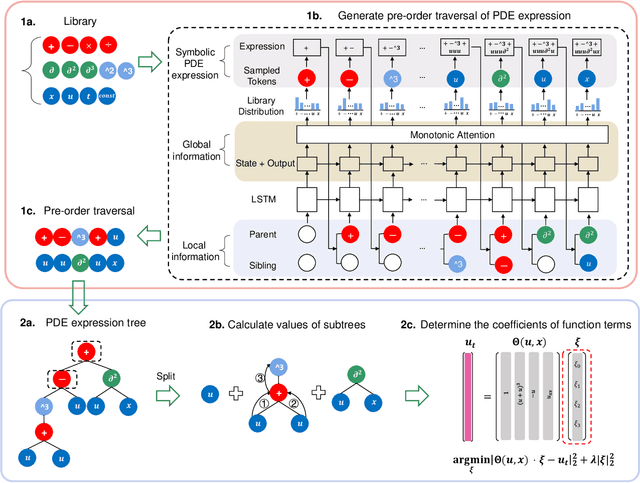
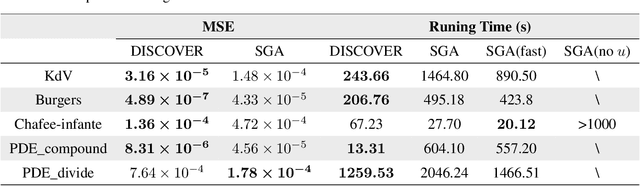
The working mechanisms of complex natural systems tend to abide by concise and profound partial differential equations (PDEs). Methods that directly mine equations from data are called PDE discovery, which reveals consistent physical laws and facilitates our interaction with the natural world. In this paper, an enhanced deep reinforcement-learning framework is proposed to uncover symbolic open-form PDEs with little prior knowledge. Specifically, (1) we first build a symbol library and define that a PDE can be represented as a tree structure. Then, (2) we design a structure-aware recurrent neural network agent by combining structured inputs and monotonic attention to generate the pre-order traversal of PDE expression trees. The expression trees are then split into function terms, and their coefficients can be calculated by the sparse regression method. (3) All of the generated PDE candidates are first filtered by some physical and mathematical constraints, and then evaluated by a meticulously designed reward function considering the fitness to data and the parsimony of the equation. (4) We adopt the risk-seeking policy gradient to iteratively update the agent to improve the best-case performance. The experiment demonstrates that our framework is capable of mining the governing equations of several canonical systems with great efficiency and scalability.

AutoKE: An automatic knowledge embedding framework for scientific machine learning

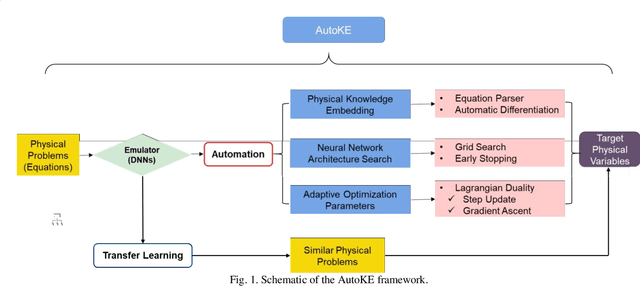
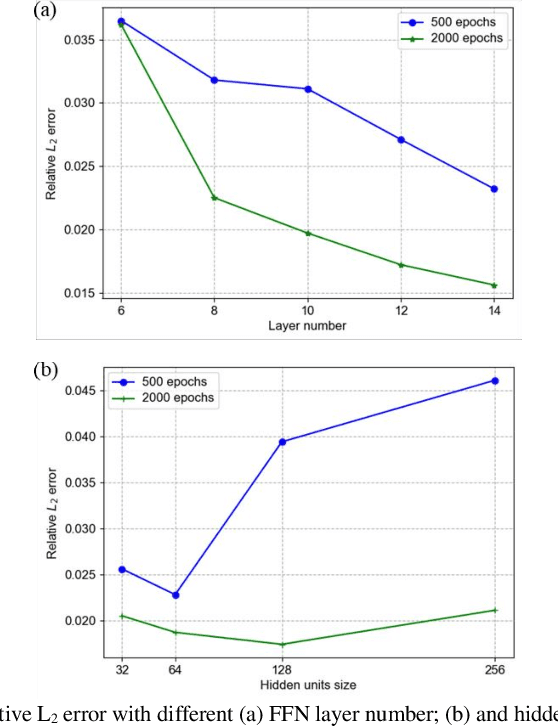
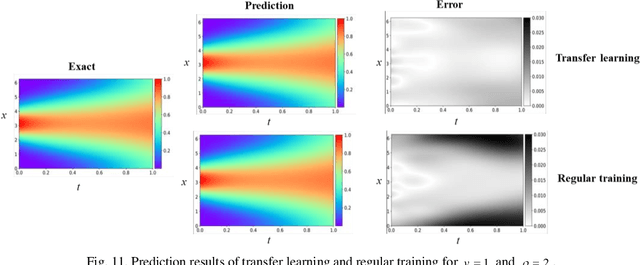
Imposing physical constraints on neural networks as a method of knowledge embedding has achieved great progress in solving physical problems described by governing equations. However, for many engineering problems, governing equations often have complex forms, including complex partial derivatives or stochastic physical fields, which results in significant inconveniences from the perspective of implementation. In this paper, a scientific machine learning framework, called AutoKE, is proposed, and a reservoir flow problem is taken as an instance to demonstrate that this framework can effectively automate the process of embedding physical knowledge. In AutoKE, an emulator comprised of deep neural networks (DNNs) is built for predicting the physical variables of interest. An arbitrarily complex equation can be parsed and automatically converted into a computational graph through the equation parser module, and the fitness of the emulator to the governing equation is evaluated via automatic differentiation. Furthermore, the fixed weights in the loss function are substituted with adaptive weights by incorporating the Lagrangian dual method. Neural architecture search (NAS) is also introduced into the AutoKE to select an optimal network architecture of the emulator according to the specific problem. Finally, we apply transfer learning to enhance the scalability of the emulator. In experiments, the framework is verified by a series of physical problems in which it can automatically embed physical knowledge into an emulator without heavy hand-coding. The results demonstrate that the emulator can not only make accurate predictions, but also be applied to similar problems with high efficiency via transfer learning.

The USTC-NELSLIP Systems for Simultaneous Speech Translation Task at IWSLT 2021

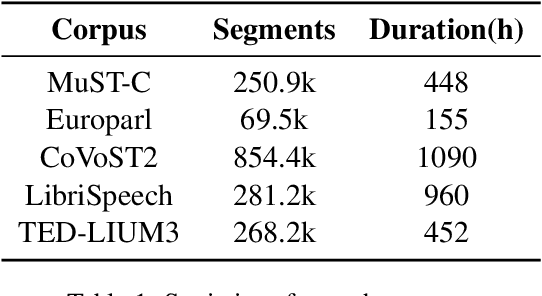
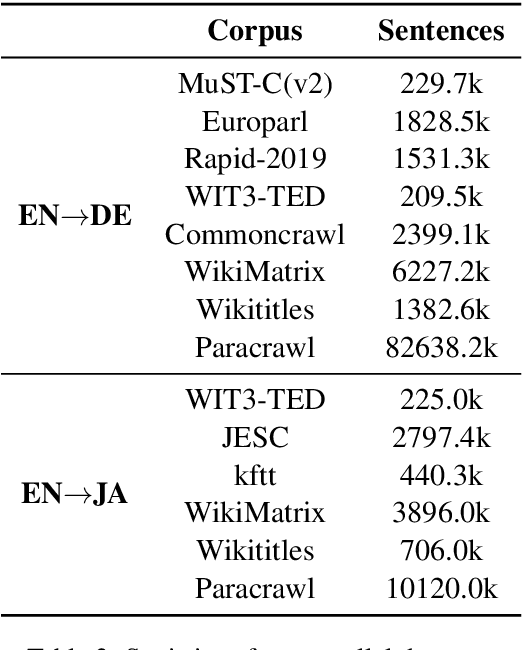
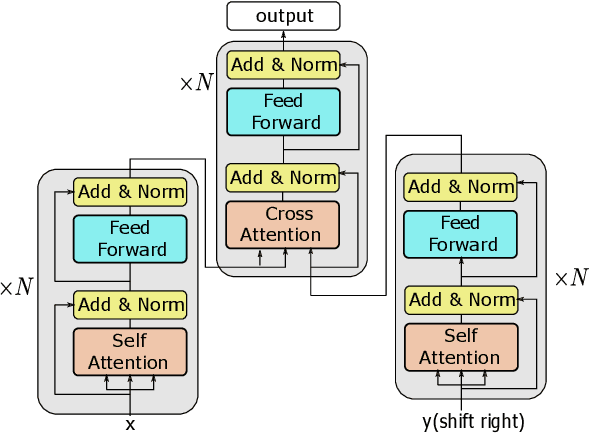
This paper describes USTC-NELSLIP's submissions to the IWSLT2021 Simultaneous Speech Translation task. We proposed a novel simultaneous translation model, Cross Attention Augmented Transducer (CAAT), which extends conventional RNN-T to sequence-to-sequence tasks without monotonic constraints, e.g., simultaneous translation. Experiments on speech-to-text (S2T) and text-to-text (T2T) simultaneous translation tasks shows CAAT achieves better quality-latency trade-offs compared to \textit{wait-k}, one of the previous state-of-the-art approaches. Based on CAAT architecture and data augmentation, we build S2T and T2T simultaneous translation systems in this evaluation campaign. Compared to last year's optimal systems, our S2T simultaneous translation system improves by an average of 11.3 BLEU for all latency regimes, and our T2T simultaneous translation system improves by an average of 4.6 BLEU.