AutoKE: An automatic knowledge embedding framework for scientific machine learning
Paper and Code
May 11, 2022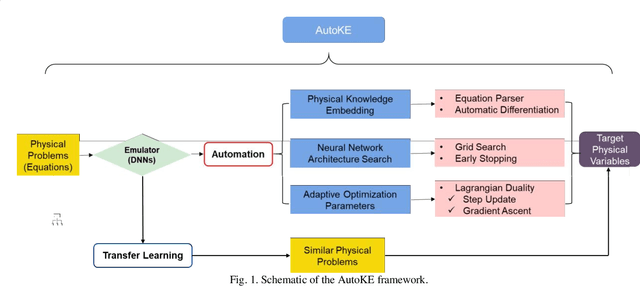
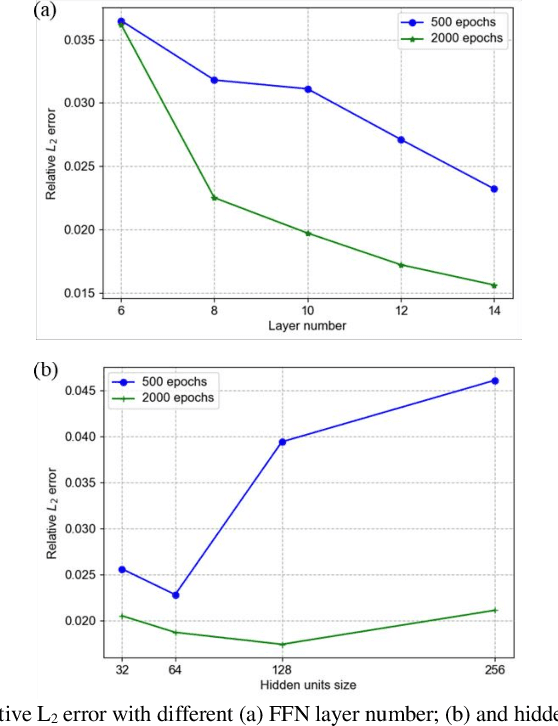
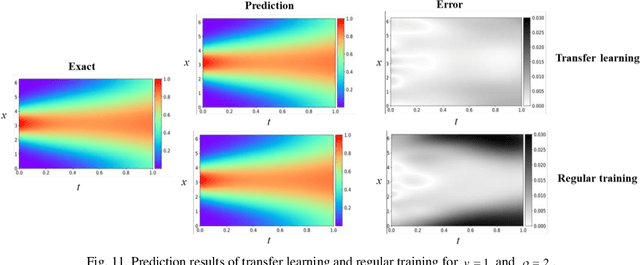

Imposing physical constraints on neural networks as a method of knowledge embedding has achieved great progress in solving physical problems described by governing equations. However, for many engineering problems, governing equations often have complex forms, including complex partial derivatives or stochastic physical fields, which results in significant inconveniences from the perspective of implementation. In this paper, a scientific machine learning framework, called AutoKE, is proposed, and a reservoir flow problem is taken as an instance to demonstrate that this framework can effectively automate the process of embedding physical knowledge. In AutoKE, an emulator comprised of deep neural networks (DNNs) is built for predicting the physical variables of interest. An arbitrarily complex equation can be parsed and automatically converted into a computational graph through the equation parser module, and the fitness of the emulator to the governing equation is evaluated via automatic differentiation. Furthermore, the fixed weights in the loss function are substituted with adaptive weights by incorporating the Lagrangian dual method. Neural architecture search (NAS) is also introduced into the AutoKE to select an optimal network architecture of the emulator according to the specific problem. Finally, we apply transfer learning to enhance the scalability of the emulator. In experiments, the framework is verified by a series of physical problems in which it can automatically embed physical knowledge into an emulator without heavy hand-coding. The results demonstrate that the emulator can not only make accurate predictions, but also be applied to similar problems with high efficiency via transfer learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge