DISCOVER: Deep identification of symbolic open-form PDEs via enhanced reinforcement-learning

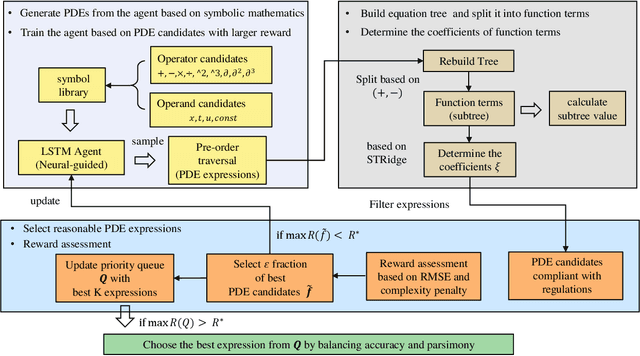
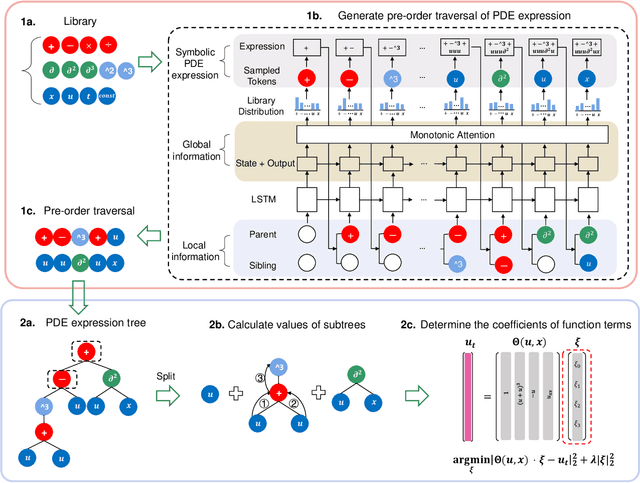
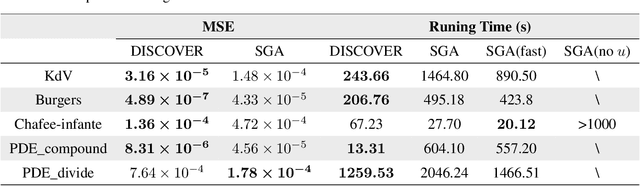
The working mechanisms of complex natural systems tend to abide by concise and profound partial differential equations (PDEs). Methods that directly mine equations from data are called PDE discovery, which reveals consistent physical laws and facilitates our interaction with the natural world. In this paper, an enhanced deep reinforcement-learning framework is proposed to uncover symbolic open-form PDEs with little prior knowledge. Specifically, (1) we first build a symbol library and define that a PDE can be represented as a tree structure. Then, (2) we design a structure-aware recurrent neural network agent by combining structured inputs and monotonic attention to generate the pre-order traversal of PDE expression trees. The expression trees are then split into function terms, and their coefficients can be calculated by the sparse regression method. (3) All of the generated PDE candidates are first filtered by some physical and mathematical constraints, and then evaluated by a meticulously designed reward function considering the fitness to data and the parsimony of the equation. (4) We adopt the risk-seeking policy gradient to iteratively update the agent to improve the best-case performance. The experiment demonstrates that our framework is capable of mining the governing equations of several canonical systems with great efficiency and scalability.