Marco Corneli
SAMM
Gaussian Embedding of Temporal Networks
May 27, 2024Abstract:Representing the nodes of continuous-time temporal graphs in a low-dimensional latent space has wide-ranging applications, from prediction to visualization. Yet, analyzing continuous-time relational data with timestamped interactions introduces unique challenges due to its sparsity. Merely embedding nodes as trajectories in the latent space overlooks this sparsity, emphasizing the need to quantify uncertainty around the latent positions. In this paper, we propose TGNE (\textbf{T}emporal \textbf{G}aussian \textbf{N}etwork \textbf{E}mbedding), an innovative method that bridges two distinct strands of literature: the statistical analysis of networks via Latent Space Models (LSM)\cite{Hoff2002} and temporal graph machine learning. TGNE embeds nodes as piece-wise linear trajectories of Gaussian distributions in the latent space, capturing both structural information and uncertainty around the trajectories. We evaluate TGNE's effectiveness in reconstructing the original graph and modelling uncertainty. The results demonstrate that TGNE generates competitive time-varying embedding locations compared to common baselines for reconstructing unobserved edge interactions based on observed edges. Furthermore, the uncertainty estimates align with the time-varying degree distribution in the network, providing valuable insights into the temporal dynamics of the graph. To facilitate reproducibility, we provide an open-source implementation of TGNE at \url{https://github.com/aida-ugent/tgne}.
Template based Graph Neural Network with Optimal Transport Distances
May 31, 2022
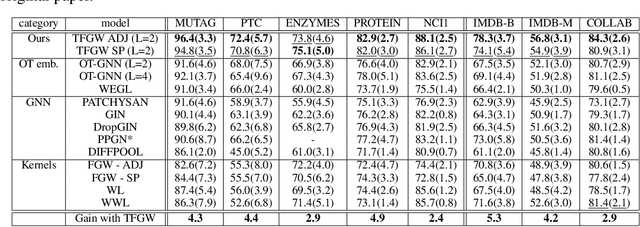
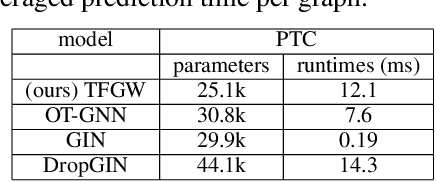

Abstract:Current Graph Neural Networks (GNN) architectures generally rely on two important components: node features embedding through message passing, and aggregation with a specialized form of pooling. The structural (or topological) information is implicitly taken into account in these two steps. We propose in this work a novel point of view, which places distances to some learnable graph templates at the core of the graph representation. This distance embedding is constructed thanks to an optimal transport distance: the Fused Gromov-Wasserstein (FGW) distance, which encodes simultaneously feature and structure dissimilarities by solving a soft graph-matching problem. We postulate that the vector of FGW distances to a set of template graphs has a strong discriminative power, which is then fed to a non-linear classifier for final predictions. Distance embedding can be seen as a new layer, and can leverage on existing message passing techniques to promote sensible feature representations. Interestingly enough, in our work the optimal set of template graphs is also learnt in an end-to-end fashion by differentiating through this layer. After describing the corresponding learning procedure, we empirically validate our claim on several synthetic and real life graph classification datasets, where our method is competitive or surpasses kernel and GNN state-of-the-art approaches. We complete our experiments by an ablation study and a sensitivity analysis to parameters.
Semi-relaxed Gromov Wasserstein divergence with applications on graphs
Oct 06, 2021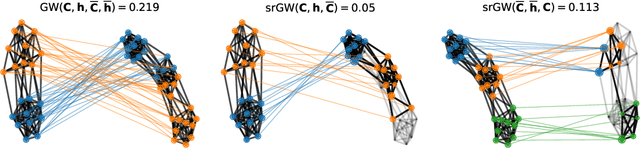
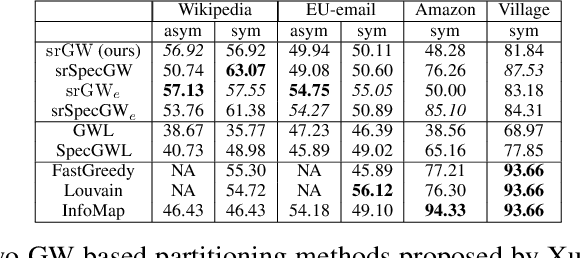
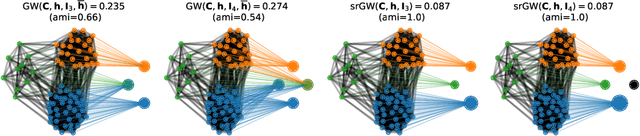
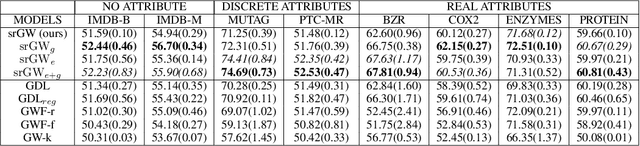
Abstract:Comparing structured objects such as graphs is a fundamental operation involved in many learning tasks. To this end, the Gromov-Wasserstein (GW) distance, based on Optimal Transport (OT), has proven to be successful in handling the specific nature of the associated objects. More specifically, through the nodes connectivity relations, GW operates on graphs, seen as probability measures over specific spaces. At the core of OT is the idea of conservation of mass, which imposes a coupling between all the nodes from the two considered graphs. We argue in this paper that this property can be detrimental for tasks such as graph dictionary or partition learning, and we relax it by proposing a new semi-relaxed Gromov-Wasserstein divergence. Aside from immediate computational benefits, we discuss its properties, and show that it can lead to an efficient graph dictionary learning algorithm. We empirically demonstrate its relevance for complex tasks on graphs such as partitioning, clustering and completion.
Continuous Latent Position Models for Instantaneous Interactions
Mar 31, 2021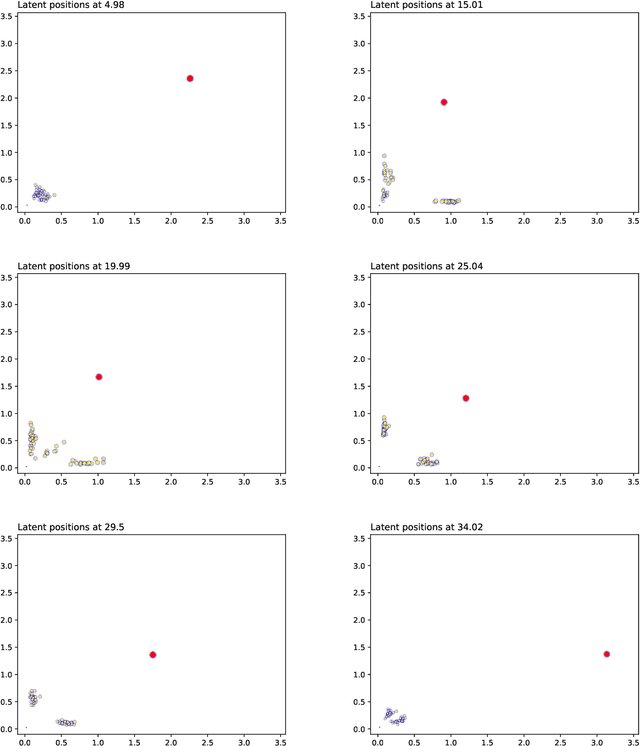
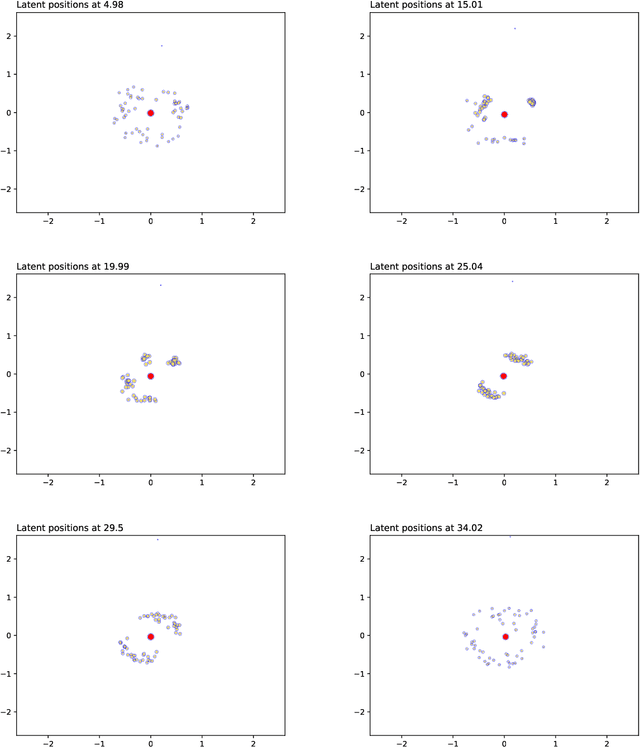
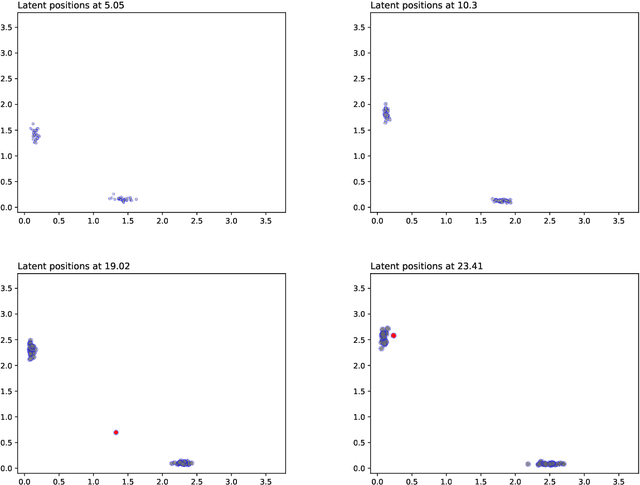
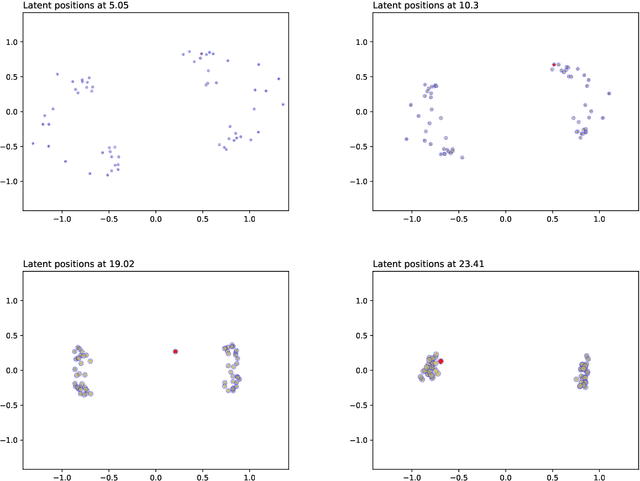
Abstract:We create a framework to analyse the timing and frequency of instantaneous interactions between pairs of entities. This type of interaction data is especially common nowadays, and easily available. Examples of instantaneous interactions include email networks, phone call networks and some common types of technological and transportation networks. Our framework relies on a novel extension of the latent position network model: we assume that the entities are embedded in a latent Euclidean space, and that they move along individual trajectories which are continuous over time. These trajectories are used to characterize the timing and frequency of the pairwise interactions. We discuss an inferential framework where we estimate the individual trajectories from the observed interaction data, and propose applications on artificial and real data.
Online Graph Dictionary Learning
Feb 12, 2021


Abstract:Dictionary learning is a key tool for representation learning, that explains the data as linear combination of few basic elements. Yet, this analysis is not amenable in the context of graph learning, as graphs usually belong to different metric spaces. We fill this gap by proposing a new online Graph Dictionary Learning approach, which uses the Gromov Wasserstein divergence for the data fitting term. In our work, graphs are encoded through their nodes' pairwise relations and modeled as convex combination of graph atoms, i.e. dictionary elements, estimated thanks to an online stochastic algorithm, which operates on a dataset of unregistered graphs with potentially different number of nodes. Our approach naturally extends to labeled graphs, and is completed by a novel upper bound that can be used as a fast approximation of Gromov Wasserstein in the embedding space. We provide numerical evidences showing the interest of our approach for unsupervised embedding of graph datasets and for online graph subspace estimation and tracking.
An Optimal Control Approach to Learning in SIDARTHE Epidemic model
Oct 28, 2020
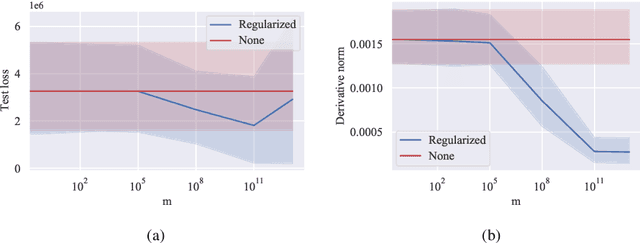
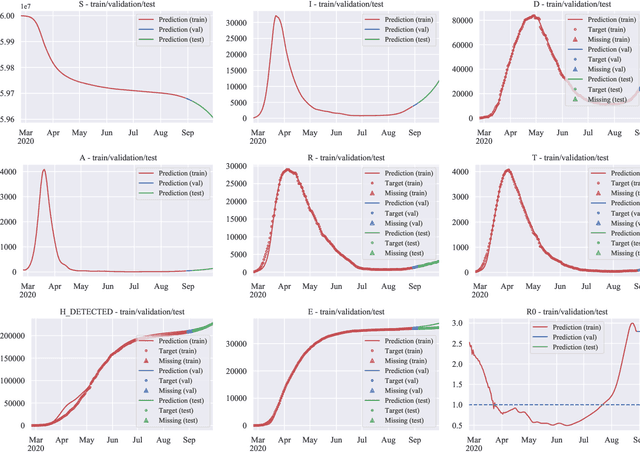
Abstract:The COVID-19 outbreak has stimulated the interest in the proposal of novel epidemiological models to predict the course of the epidemic so as to help planning effective control strategies. In particular, in order to properly interpret the available data, it has become clear that one must go beyond most classic epidemiological models and consider models that, like the recently proposed SIDARTHE, offer a richer description of the stages of infection. The problem of learning the parameters of these models is of crucial importance especially when assuming that they are time-variant, which further enriches their effectiveness. In this paper we propose a general approach for learning time-variant parameters of dynamic compartmental models from epidemic data. We formulate the problem in terms of a functional risk that depends on the learning variables through the solutions of a dynamic system. The resulting variational problem is then solved by using a gradient flow on a suitable, regularized functional. We forecast the epidemic evolution in Italy and France. Results indicate that the model provides reliable and challenging predictions over all available data as well as the fundamental role of the chosen strategy on the time-variant parameters.
From text saliency to linguistic objects: learning linguistic interpretable markers with a multi-channels convolutional architecture
Apr 07, 2020
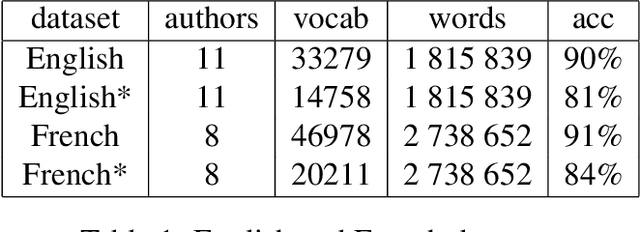
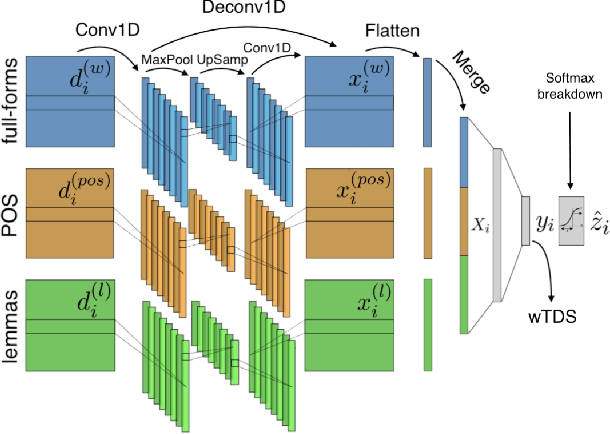
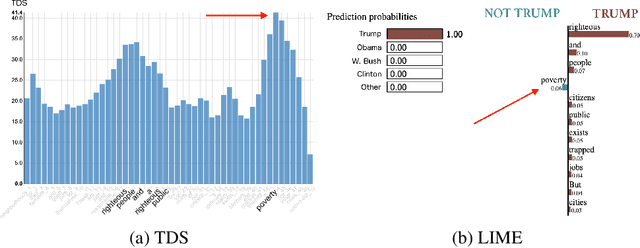
Abstract:A lot of effort is currently made to provide methods to analyze and understand deep neural network impressive performances for tasks such as image or text classification. These methods are mainly based on visualizing the important input features taken into account by the network to build a decision. However these techniques, let us cite LIME, SHAP, Grad-CAM, or TDS, require extra effort to interpret the visualization with respect to expert knowledge. In this paper, we propose a novel approach to inspect the hidden layers of a fitted CNN in order to extract interpretable linguistic objects from texts exploiting classification process. In particular, we detail a weighted extension of the Text Deconvolution Saliency (wTDS) measure which can be used to highlight the relevant features used by the CNN to perform the classification task. We empirically demonstrate the efficiency of our approach on corpora from two different languages: English and French. On all datasets, wTDS automatically encodes complex linguistic objects based on co-occurrences and possibly on grammatical and syntax analysis.
Block modelling in dynamic networks with non-homogeneous Poisson processes and exact ICL
Jul 10, 2017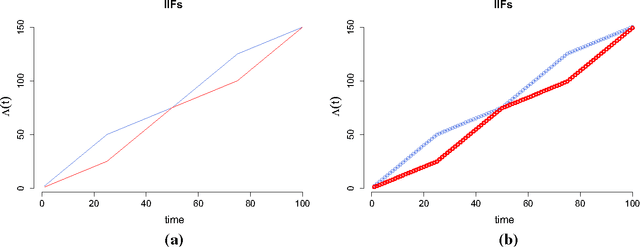
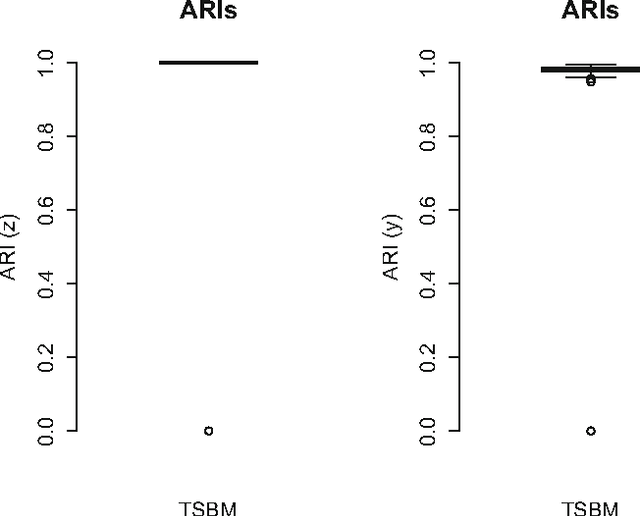
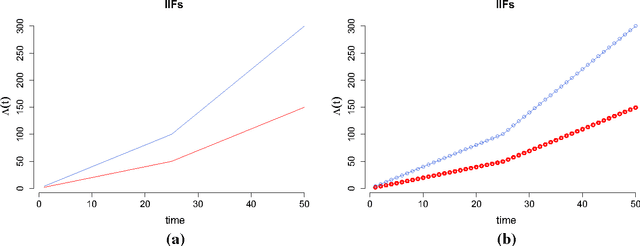
Abstract:We develop a model in which interactions between nodes of a dynamic network are counted by non homogeneous Poisson processes. In a block modelling perspective, nodes belong to hidden clusters (whose number is unknown) and the intensity functions of the counting processes only depend on the clusters of nodes. In order to make inference tractable we move to discrete time by partitioning the entire time horizon in which interactions are observed in fixed-length time sub-intervals. First, we derive an exact integrated classification likelihood criterion and maximize it relying on a greedy search approach. This allows to estimate the memberships to clusters and the number of clusters simultaneously. Then a maximum-likelihood estimator is developed to estimate non parametrically the integrated intensities. We discuss the over-fitting problems of the model and propose a regularized version solving these issues. Experiments on real and simulated data are carried out in order to assess the proposed methodology.
Exact ICL maximization in a non-stationary temporal extension of the stochastic block model for dynamic networks
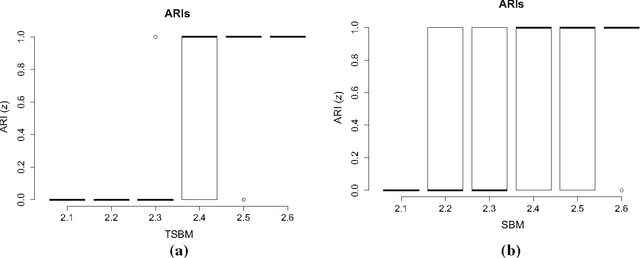
Jul 10, 2017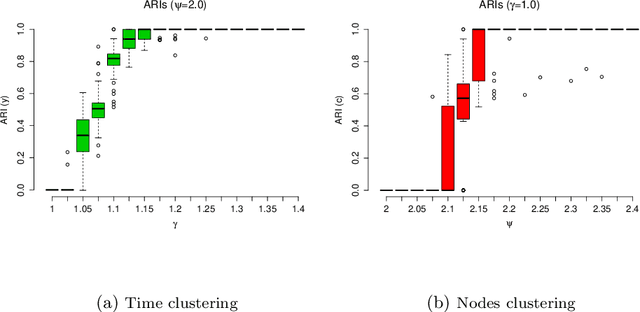
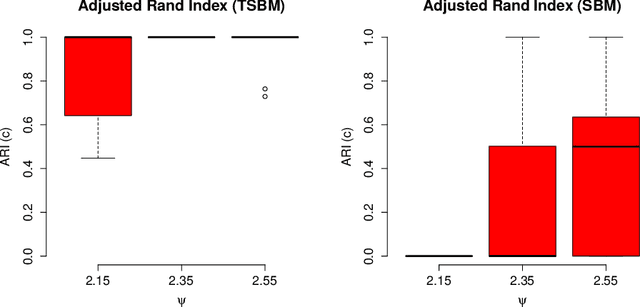
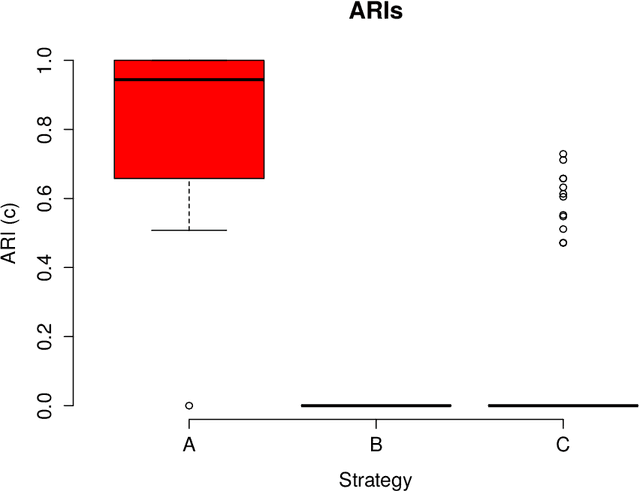
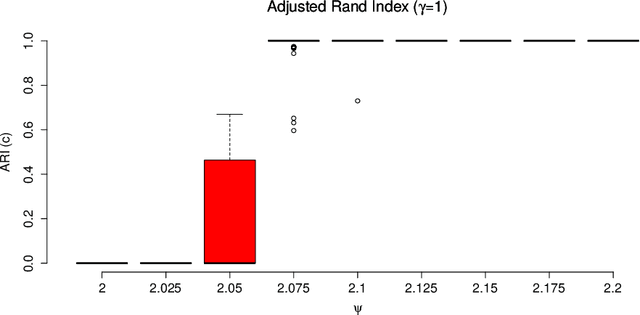
Abstract:The stochastic block model (SBM) is a flexible probabilistic tool that can be used to model interactions between clusters of nodes in a network. However, it does not account for interactions of time varying intensity between clusters. The extension of the SBM developed in this paper addresses this shortcoming through a temporal partition: assuming interactions between nodes are recorded on fixed-length time intervals, the inference procedure associated with the model we propose allows to cluster simultaneously the nodes of the network and the time intervals. The number of clusters of nodes and of time intervals, as well as the memberships to clusters, are obtained by maximizing an exact integrated complete-data likelihood, relying on a greedy search approach. Experiments on simulated and real data are carried out in order to assess the proposed methodology.
Modelling time evolving interactions in networks through a non stationary extension of stochastic block models
Sep 08, 2015
Abstract:In this paper, we focus on the stochastic block model (SBM),a probabilistic tool describing interactions between nodes of a network using latent clusters. The SBM assumes that the networkhas a stationary structure, in which connections of time varying intensity are not taken into account. In other words, interactions between two groups are forced to have the same features during the whole observation time. To overcome this limitation,we propose a partition of the whole time horizon, in which interactions are observed, and develop a non stationary extension of the SBM,allowing to simultaneously cluster the nodes in a network along with fixed time intervals in which the interactions take place. The number of clusters (K for nodes, D for time intervals) as well as the class memberships are finallyobtained through maximizing the complete-data integrated likelihood by means of a greedy search approach. After showing that the model works properly with simulated data, we focus on a real data set. We thus consider the three days ACM Hypertext conference held in Turin,June 29th - July 1st 2009. Proximity interactions between attendees during the first day are modelled and an interestingclustering of the daily hours is finally obtained, with times of social gathering (e.g. coffee breaks) recovered by the approach. Applications to large networks are limited due to the computational complexity of the greedy search which is dominated bythe number $K\_{max}$ and $D\_{max}$ of clusters used in the initialization. Therefore,advanced clustering tools are considered to reduce the number of clusters expected in the data, making the greedy search applicable to large networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge