How Predicted Links Influence Network Evolution: Disentangling Choice and Algorithmic Feedback in Dynamic Graphs

Link prediction models are increasingly used to recommend interactions in evolving networks, yet their impact on network structure is typically assessed from static snapshots. In particular, observed homophily conflates intrinsic interaction tendencies with amplification effects induced by network dynamics and algorithmic feedback. We propose a temporal framework based on multivariate Hawkes processes that disentangles these two sources and introduce an instantaneous bias measure derived from interaction intensities, capturing current reinforcement dynamics beyond cumulative metrics. We provide a theoretical characterization of the stability and convergence of the induced dynamics, and experiments show that the proposed measure reliably reflects algorithmic feedback effects across different link prediction strategies.

Gaussian Embedding of Temporal Networks

Representing the nodes of continuous-time temporal graphs in a low-dimensional latent space has wide-ranging applications, from prediction to visualization. Yet, analyzing continuous-time relational data with timestamped interactions introduces unique challenges due to its sparsity. Merely embedding nodes as trajectories in the latent space overlooks this sparsity, emphasizing the need to quantify uncertainty around the latent positions. In this paper, we propose TGNE (\textbf{T}emporal \textbf{G}aussian \textbf{N}etwork \textbf{E}mbedding), an innovative method that bridges two distinct strands of literature: the statistical analysis of networks via Latent Space Models (LSM)\cite{Hoff2002} and temporal graph machine learning. TGNE embeds nodes as piece-wise linear trajectories of Gaussian distributions in the latent space, capturing both structural information and uncertainty around the trajectories. We evaluate TGNE's effectiveness in reconstructing the original graph and modelling uncertainty. The results demonstrate that TGNE generates competitive time-varying embedding locations compared to common baselines for reconstructing unobserved edge interactions based on observed edges. Furthermore, the uncertainty estimates align with the time-varying degree distribution in the network, providing valuable insights into the temporal dynamics of the graph. To facilitate reproducibility, we provide an open-source implementation of TGNE at \url{https://github.com/aida-ugent/tgne}.

Exploring the Performance of Continuous-Time Dynamic Link Prediction Algorithms

Dynamic Link Prediction (DLP) addresses the prediction of future links in evolving networks. However, accurately portraying the performance of DLP algorithms poses challenges that might impede progress in the field. Importantly, common evaluation pipelines usually calculate ranking or binary classification metrics, where the scores of observed interactions (positives) are compared with those of randomly generated ones (negatives). However, a single metric is not sufficient to fully capture the differences between DLP algorithms, and is prone to overly optimistic performance evaluation. Instead, an in-depth evaluation should reflect performance variations across different nodes, edges, and time segments. In this work, we contribute tools to perform such a comprehensive evaluation. (1) We propose Birth-Death diagrams, a simple but powerful visualization technique that illustrates the effect of time-based train-test splitting on the difficulty of DLP on a given dataset. (2) We describe an exhaustive taxonomy of negative sampling methods that can be used at evaluation time. (3) We carry out an empirical study of the effect of the different negative sampling strategies. Our comparison between heuristics and state-of-the-art memory-based methods on various real-world datasets confirms a strong effect of using different negative sampling strategies on the test Area Under the Curve (AUC). Moreover, we conduct a visual exploration of the prediction, with additional insights on which different types of errors are prominent over time.

New Perspectives on the Evaluation of Link Prediction Algorithms for Dynamic Graphs

There is a fast-growing body of research on predicting future links in dynamic networks, with many new algorithms. Some benchmark data exists, and performance evaluations commonly rely on comparing the scores of observed network events (positives) with those of randomly generated ones (negatives). These evaluation measures depend on both the predictive ability of the model and, crucially, the type of negative samples used. Besides, as generally the case with temporal data, prediction quality may vary over time. This creates a complex evaluation space. In this work, we catalog the possibilities for negative sampling and introduce novel visualization methods that can yield insight into prediction performance and the dynamics of temporal networks. We leverage these visualization tools to investigate the effect of negative sampling on the predictive performance, at the node and edge level. We validate empirically, on datasets extracted from recent benchmarks that the error is typically not evenly distributed across different data segments. Finally, we argue that such visualization tools can serve as powerful guides to evaluate dynamic link prediction methods at different levels.

Graph-Survival: A Survival Analysis Framework for Machine Learning on Temporal Networks

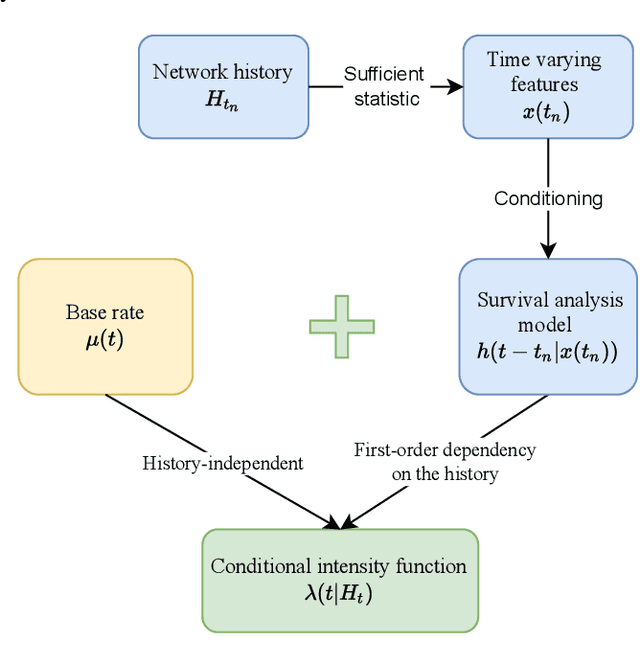
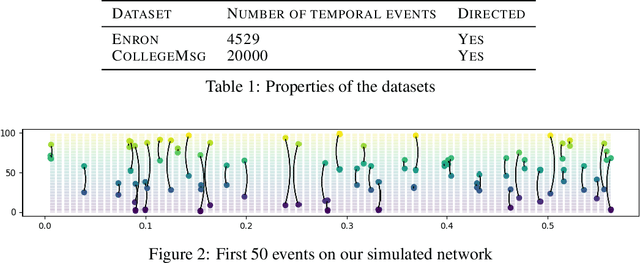
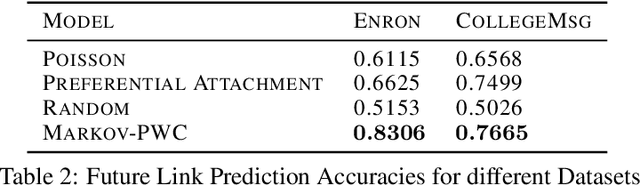
Continuous time temporal networks are attracting increasing attention due their omnipresence in real-world datasets and they manifold applications. While static network models have been successful in capturing static topological regularities, they often fail to model effects coming from the causal nature that explain the generation of networks. Exploiting the temporal aspect of networks has thus been the focus of various studies in the last decades. We propose a framework for designing generative models for continuous time temporal networks. Assuming a first order Markov assumption on the edge-specific temporal point processes enables us to flexibly apply survival analysis models directly on the waiting time between events, while using time-varying history-based features as covariates for these predictions. This approach links the well-documented field of temporal networks analysis through multivariate point processes, with methodological tools adapted from survival analysis. We propose a fitting method for models within this framework, and an algorithm for simulating new temporal networks having desired properties. We evaluate our method on a downstream future link prediction task, and provide a qualitative assessment of the network simulations.