Lubor Ladicky
Discrete Optimization of Ray Potentials for Semantic 3D Reconstruction
Jun 25, 2019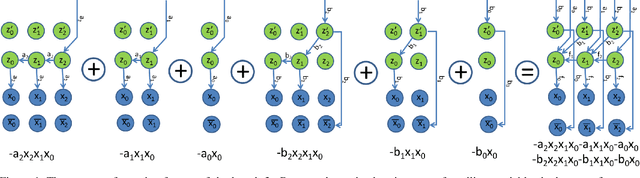
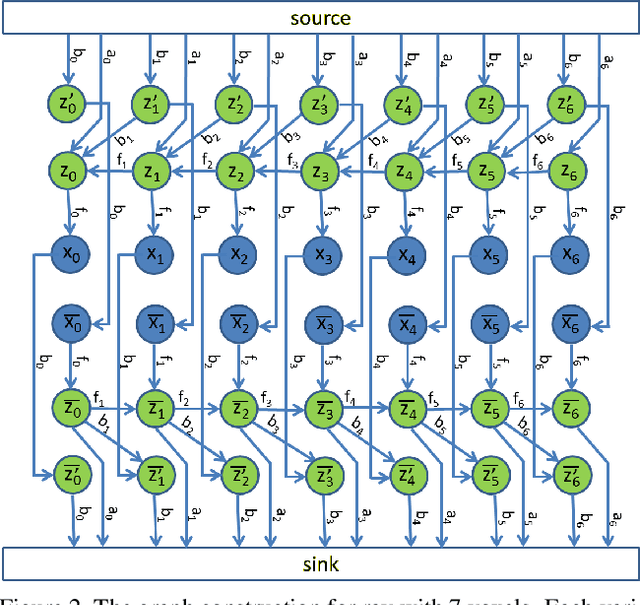

Abstract:Dense semantic 3D reconstruction is typically formulated as a discrete or continuous problem over label assignments in a voxel grid, combining semantic and depth likelihoods in a Markov Random Field framework. The depth and semantic information is incorporated as a unary potential, smoothed by a pairwise regularizer. However, modelling likelihoods as a unary potential does not model the problem correctly leading to various undesirable visibility artifacts. We propose to formulate an optimization problem that directly optimizes the reprojection error of the 3D model with respect to the image estimates, which corresponds to the optimization over rays, where the cost function depends on the semantic class and depth of the first occupied voxel along the ray. The 2-label formulation is made feasible by transforming it into a graph-representable form under QPBO relaxation, solvable using graph cut. The multi-label problem is solved by applying alpha-expansion using the same relaxation in each expansion move. Our method was indeed shown to be feasible in practice, running comparably fast to the competing methods, while not suffering from ray potential approximation artifacts.
Matching neural paths: transfer from recognition to correspondence search
Nov 05, 2017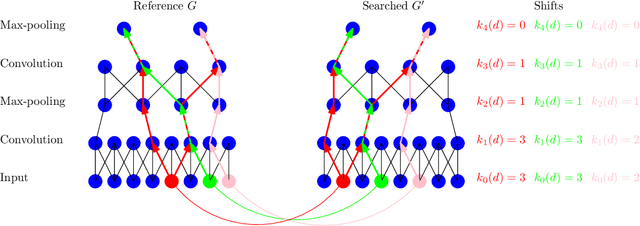

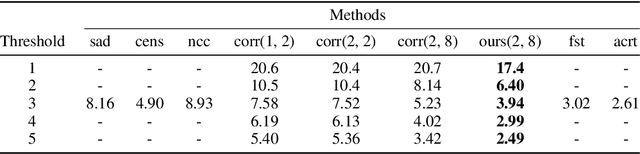
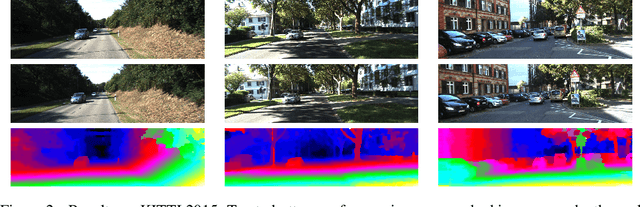
Abstract:Many machine learning tasks require finding per-part correspondences between objects. In this work we focus on low-level correspondences - a highly ambiguous matching problem. We propose to use a hierarchical semantic representation of the objects, coming from a convolutional neural network, to solve this ambiguity. Training it for low-level correspondence prediction directly might not be an option in some domains where the ground-truth correspondences are hard to obtain. We show how transfer from recognition can be used to avoid such training. Our idea is to mark parts as "matching" if their features are close to each other at all the levels of convolutional feature hierarchy (neural paths). Although the overall number of such paths is exponential in the number of layers, we propose a polynomial algorithm for aggregating all of them in a single backward pass. The empirical validation is done on the task of stereo correspondence and demonstrates that we achieve competitive results among the methods which do not use labeled target domain data.
Semantic3D.net: A new Large-scale Point Cloud Classification Benchmark
Apr 12, 2017

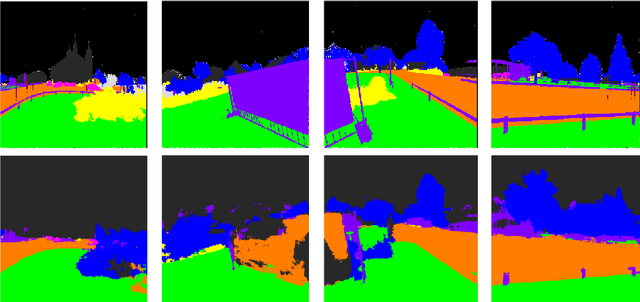

Abstract:This paper presents a new 3D point cloud classification benchmark data set with over four billion manually labelled points, meant as input for data-hungry (deep) learning methods. We also discuss first submissions to the benchmark that use deep convolutional neural networks (CNNs) as a work horse, which already show remarkable performance improvements over state-of-the-art. CNNs have become the de-facto standard for many tasks in computer vision and machine learning like semantic segmentation or object detection in images, but have no yet led to a true breakthrough for 3D point cloud labelling tasks due to lack of training data. With the massive data set presented in this paper, we aim at closing this data gap to help unleash the full potential of deep learning methods for 3D labelling tasks. Our semantic3D.net data set consists of dense point clouds acquired with static terrestrial laser scanners. It contains 8 semantic classes and covers a wide range of urban outdoor scenes: churches, streets, railroad tracks, squares, villages, soccer fields and castles. We describe our labelling interface and show that our data set provides more dense and complete point clouds with much higher overall number of labelled points compared to those already available to the research community. We further provide baseline method descriptions and comparison between methods submitted to our online system. We hope semantic3D.net will pave the way for deep learning methods in 3D point cloud labelling to learn richer, more general 3D representations, and first submissions after only a few months indicate that this might indeed be the case.
Quad-networks: unsupervised learning to rank for interest point detection
Apr 10, 2017
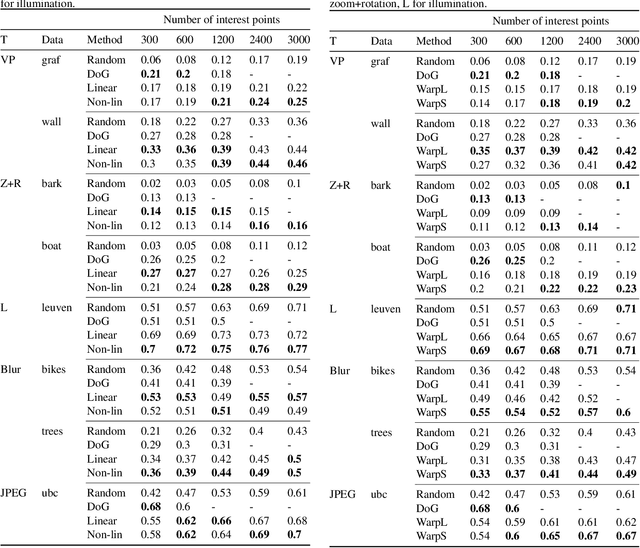
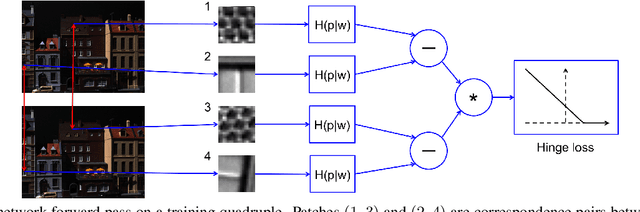

Abstract:Several machine learning tasks require to represent the data using only a sparse set of interest points. An ideal detector is able to find the corresponding interest points even if the data undergo a transformation typical for a given domain. Since the task is of high practical interest in computer vision, many hand-crafted solutions were proposed. In this paper, we ask a fundamental question: can we learn such detectors from scratch? Since it is often unclear what points are "interesting", human labelling cannot be used to find a truly unbiased solution. Therefore, the task requires an unsupervised formulation. We are the first to propose such a formulation: training a neural network to rank points in a transformation-invariant manner. Interest points are then extracted from the top/bottom quantiles of this ranking. We validate our approach on two tasks: standard RGB image interest point detection and challenging cross-modal interest point detection between RGB and depth images. We quantitatively show that our unsupervised method performs better or on-par with baselines.
Efficient Minimization of Higher Order Submodular Functions using Monotonic Boolean Functions
Jan 23, 2017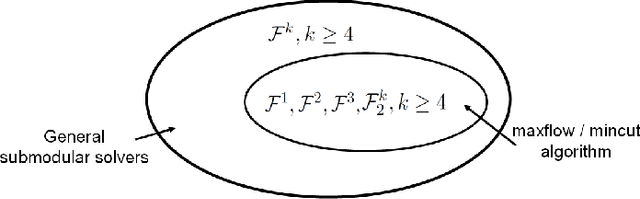
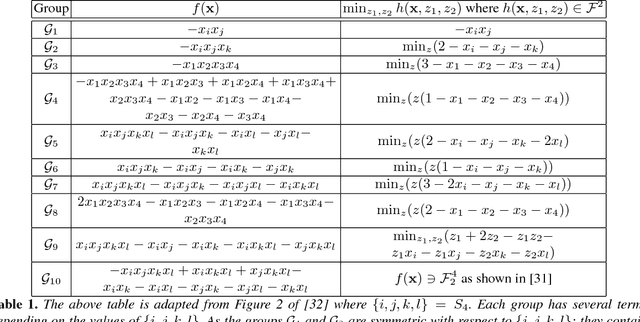

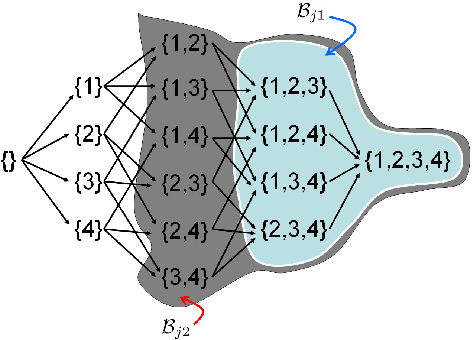
Abstract:Submodular function minimization is a key problem in a wide variety of applications in machine learning, economics, game theory, computer vision, and many others. The general solver has a complexity of $O(n^3 \log^2 n . E +n^4 {\log}^{O(1)} n)$ where $E$ is the time required to evaluate the function and $n$ is the number of variables \cite{Lee2015}. On the other hand, many computer vision and machine learning problems are defined over special subclasses of submodular functions that can be written as the sum of many submodular cost functions defined over cliques containing few variables. In such functions, the pseudo-Boolean (or polynomial) representation \cite{BorosH02} of these subclasses are of degree (or order, or clique size) $k$ where $k \ll n$. In this work, we develop efficient algorithms for the minimization of this useful subclass of submodular functions. To do this, we define novel mapping that transform submodular functions of order $k$ into quadratic ones. The underlying idea is to use auxiliary variables to model the higher order terms and the transformation is found using a carefully constructed linear program. In particular, we model the auxiliary variables as monotonic Boolean functions, allowing us to obtain a compact transformation using as few auxiliary variables as possible.
Semantic 3D Reconstruction with Continuous Regularization and Ray Potentials Using a Visibility Consistency Constraint
May 22, 2016

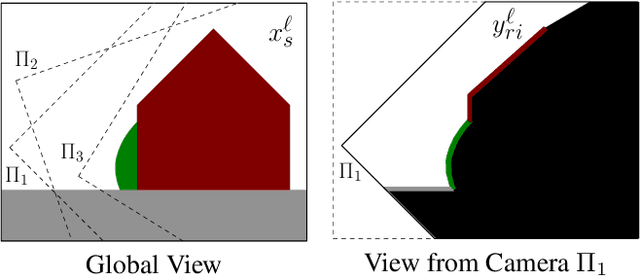

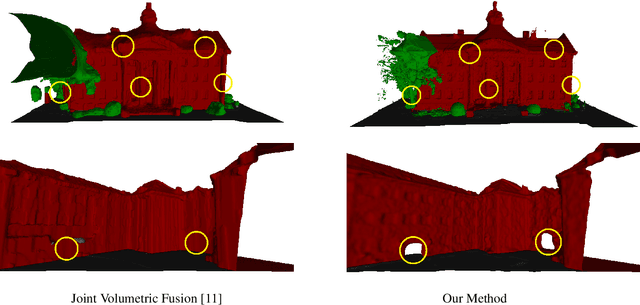
Abstract:We propose an approach for dense semantic 3D reconstruction which uses a data term that is defined as potentials over viewing rays, combined with continuous surface area penalization. Our formulation is a convex relaxation which we augment with a crucial non-convex constraint that ensures exact handling of visibility. To tackle the non-convex minimization problem, we propose a majorize-minimize type strategy which converges to a critical point. We demonstrate the benefits of using the non-convex constraint experimentally. For the geometry-only case, we set a new state of the art on two datasets of the commonly used Middlebury multi-view stereo benchmark. Moreover, our general-purpose formulation directly reconstructs thin objects, which are usually treated with specialized algorithms. A qualitative evaluation on the dense semantic 3D reconstruction task shows that we improve significantly over previous methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge