Discrete Optimization of Ray Potentials for Semantic 3D Reconstruction

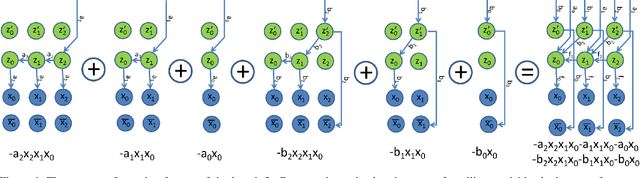
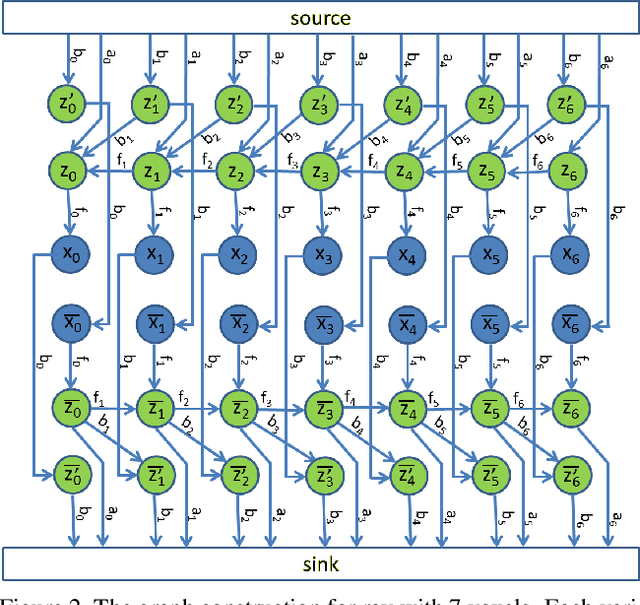
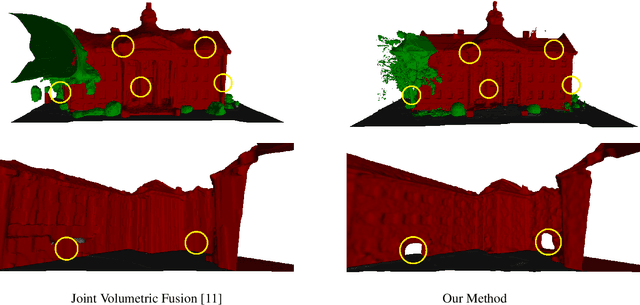
Dense semantic 3D reconstruction is typically formulated as a discrete or continuous problem over label assignments in a voxel grid, combining semantic and depth likelihoods in a Markov Random Field framework. The depth and semantic information is incorporated as a unary potential, smoothed by a pairwise regularizer. However, modelling likelihoods as a unary potential does not model the problem correctly leading to various undesirable visibility artifacts. We propose to formulate an optimization problem that directly optimizes the reprojection error of the 3D model with respect to the image estimates, which corresponds to the optimization over rays, where the cost function depends on the semantic class and depth of the first occupied voxel along the ray. The 2-label formulation is made feasible by transforming it into a graph-representable form under QPBO relaxation, solvable using graph cut. The multi-label problem is solved by applying alpha-expansion using the same relaxation in each expansion move. Our method was indeed shown to be feasible in practice, running comparably fast to the competing methods, while not suffering from ray potential approximation artifacts.